Geometry - Mensuration - Previous Year CAT/MBA Questions
The best way to prepare for Geometry - Mensuration is by going through the previous year Geometry - Mensuration XAT questions. Here we bring you all previous year Geometry - Mensuration XAT questions along with detailed solutions.
Click here for previous year questions of other topics.
It would be best if you clear your concepts before you practice previous year Geometry - Mensuration XAT questions.
A farmer has a triangular plot of land. One side of the plot, henceforth called the base, is 300 feet long and the other two sides are equal. The perpendicular distance, from the corner of the plot, where the two equal sides meet, to the base, is 200 feet. To counter the adverse effect of climate change, the farmer wants to dig a circular pond. He plans that half of the circular area will be inside the triangular plot and the other half will be outside, which he will purchase at the market rate from his neighbour. The diameter of the circular plot is entirely contained in the base and the circumference of the pond touches the two equal sides of the triangle from inside.
If the market rate per square feet of land is Rs. 1400, how much does the farmer must pay to buy the land from his neighbour for the pond? (Choose the closest option.)
- (a)
Rs. 3,16,80,000
- (b)
Rs. 4,25,60,000
- (c)
Rs. 6,33,60,000
- (d)
Rs. 7,42,80,000
- (e)
Rs. 2,98,20,000
Answer: Option A
Text Explanation :
Workspace:
A non-flying ant wants to travel from the bottom corner to the diagonally opposite top corner of a cubical room. The side of the room is 2 meters. What will be the minimum distance that the ant needs to travel?
- (a)
6 meters
- (b)
(2√2 + 2) meters
- (c)
2√3 meters
- (d)
2√6 meters
- (e)
2√5 meters
Answer: Option E
Text Explanation :
In a 2D plane, minimum distance between 2 points is the straight line joining these points.
We can convert the cubical room in a 2D plane as shown in the figure.

∴ Shortest route from A to F = = 2√5.
Hence, option (e).
Workspace:
A rectangular swimming pool is 50 meters long and 25 meters wide. Its depth is always the same along its width but linearly increases along its length from 1 meter at one end to 4 meters at the other end. How much water (in cubic meters) is needed to completely fill the pool?
- (a)
3750
- (b)
2500
- (c)
1250
- (d)
1874
- (e)
3125
Answer: Option E
Text Explanation :

Volume of the tank = Volume of the cuboid + Volume of the triangular prism
The volume of cuboid will be 50 × 25 × 1 = 1250
The volume of triangular prism = Area of triangle × width = 1/2 × 3 × 50 × 25 = 1875
∴ Total volume = 1875 + 1250 = 3125.
Hence, option (e).
Workspace:
Six drums are used to store water. Five drums are of equal capacity, while the sixth drum has double the capacity of each of these five drums. On one morning, three drums are found half full, two are found two-thirds full and one is found completely full. It is attempted to transfer all the water to the smaller drums. How many smaller drums are adequate to store the water?
- (a)
Four but not three
- (b)
Three or four, depending on which drum had how much water initially
- (c)
Five but not four
- (d)
Five may be inadequate, depending on which drum had how much water initially
- (e)
Three but not two
Answer: Option C
Text Explanation :
Let the volume of 5 smaller drums be V
∴ Volume of the bigger drum = 2V
On one morning, three drums are found half full, two are found two-thirds full and one is found completely full.
Case 1: We will get the maximum water when the bigger drum is completely full
∴ Amount of water = 3 × V/2 + 2 × 2V/3 + 1 × 2V = 29V/6 = 4.83V
∴ Number of smaller drums required to store 29V/6 water = 5
Case 2: We will get the minimum water when the bigger drum is only half full
∴ Amount of water = 1 × 2V/2 + 2 × V/2 + 2 × 2V/3 + 1 × V = 13V/3 = 4.133V
∴ Number of smaller drums required to store 13V/3 water = 5
∴ In both cases we need at least 5 smaller drums to store the water.
Hence, option (c).
Workspace:
A gold ingot in the shape of a cylinder is melted and the resulting molten metal molded into a few identical conical ingots. If the height of each cone is half the height of the original cylinder and the area of the circular base of each cone is one fifth that of the circular base of the cylinder, then how many conical ingots can be made?
- (a)
40
- (b)
30
- (c)
60
- (d)
20
- (e)
10
Answer: Option B
Text Explanation :
Volume of a cylinder = π × (base area) × height
Volume of a cylinder = 1/3 × π × (base area) × height
Volume of a cone with same base and height as that of a cylinder is 1/3rd the volume of the cylinder.
If height of the cone is half that of the cylinder, volume will also become half. Also, if the base area is 1/5th the volume will also be 1/5th.
∴ Volume of the given cone = 1/3 × 1/2 × 1/5 = 1/30th the volume of the original cylinder.
∴ 30 such cones can be made from the original cylinder.
Alternately,
Let A and h be the base area and height of the cylinder.
Base area of the cone = A/5 and height = h/2
Volume of a cylinder (V) = πAh
Volume of a cylinder = 1/3 × π × A/5 × h/2 = πAh/30 = V/30
∴ Volume of the given cone is 1/30th the volume of the cylinder.
⇒ 30 such cones can be made from the original cylinder.
Hence, option (b).
Workspace:
It takes 2 liters to paint the surface of a solid sphere. If this solid sphere is sliced into 4 identical pieces, how many liters will be required to paint all the surfaces of these 4 pieces.
- (a)
2.2 liters
- (b)
2.5 liters
- (c)
3 liters
- (d)
4 liters
- (e)
None of the above
Answer: Option D
Text Explanation :
Total outer surface area of a sphere of radius r = 4πr2
When the sphere is cut into 4 identical pieces, each piece will expose πr2/2 + πr2/2 = πr2 area more.
∴ Now, 4πr2 additional area needs to be painted which will require 2 more liters of paint.
∴ 4 litres of paint will be needed.
Hence, option (d).
Workspace:
A cone of radius 4 cm with a slant height of 12 cm was sliced horizontally, resulting into a smaller cone (upper portion) and a frustum (lower portion). If the ratio of the curved surface area of the upper smaller cone and the lower frustum is 1:2, what will be the slant height of the frustum?
- (a)
12 - √3
- (b)
12 - 2√3
- (c)
12 - 3√3
- (d)
12 - 4√3
- (e)
None of the above
Answer: Option D
Text Explanation :
Curved surface area of the original larger cone = π × Radius × Slant height = 48π
Therefore, the curved surface of the smaller cone = 1/3 × 48π = 16π
Now, the radius and slant of height of the smaller cone would be reduced in equal proportions from the larger cone.
Therefore, slant height of the frustum would be 1/√3 time the corresponding values of the larger cone.
⇒ Slant height of the smaller cone = 1/√3 × 12 = 4√3
∴ Slant height of the frustum = 12 - 4√3
Hence, option (d).
Workspace:
The Volume of a pyramid with a square base is 200 cubic cm. The height of the pyramid is 13 cm. What will be the length of the slant edges (i.e. the distance between the apex and any other vertex), rounded to the nearest integer?
- (a)
12 cm
- (b)
13 cm
- (c)
14 cm
- (d)
15 cm
- (e)
16 cm
Answer: Option C
Text Explanation :
Let the side of the square base AB = BC = CD = DA = ‘a’.
Height OB = 13.
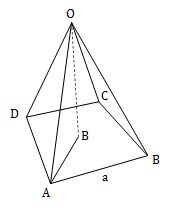
Volume of a square base pyramid = a2 × h/3 = 200 cm3
⇒ a2 = 600/13
Diagonal AC = a√2
⇒ AB = a/√2
In right ∆OAB, AO2 = AB2 + OB2
⇒ AO2 = (a/√2)2 + 132
⇒ AO2 = a2/2 + 169
⇒ AO2 = 300/13 + 169 = 2497/13
⇒ AO ≈ 13.86
Thus, the length of the slant slope (when rounded to the nearest integer) = 14 cm
Hence, option (c).
Workspace:
ABCD is a rectangle. P, Q and R are the midpoint of BC, CD and DA. The point S lies on the line QR in such a way that SR: QS = 1:3. The ratio of the area of triangle APS to area of rectangle ABCD is
- (a)
36/128
- (b)
39/128
- (c)
44/128
- (d)
48/128
- (e)
64/128
Answer: Option A
Text Explanation :
Let the length of the rectangle be ‘l’ and breadth be ‘b’.
The given figure is.

Let us draw a line MS parallel to DC

∆RMS ~ ∆RDQ
∴ RM : MD = RS : SQ = 1 : 3
Let the length of the rectangle (i.e., AB = CD) ABCD be 8l and width be 8b (i.e., AD = BC).
∴ AR = 4b and RM = b
Also, MS = l and SL = 7l.
Also, PL : LC = 1 : 3 [∵ RS : SQ = 1 : 3]
Area (∆ARS) = ½ × AR × SM = 2lb
Area (∆RDQ) = ½ × RD × DQ = 8lb
Area (∆ABP) = ½ × AB × BP = 16lb
Area (PSQC) = Area (∆PSL) + Area(∆SLQC)
= ½ × SL × PL + ½ × (SL + QC) × LC
= 3.5lb + 16.5lb
= 20lb
Area of ∆ASP = Area of rectangle ABCD – [Area (∆ARS) + Area (∆RDQ) + Area (∆ABP) + Area (PSQC)]
= 64lb – [2lb + 8lb + 16lb + 20lb]
= 64lb - 46lb = 18lb
∴ = =
Hence, option (a).
Workspace:
Akhtar plans to cover a rectangular floor of dimensions 9.5 meters and 11.5 meters using tiles. Two types of square shaped tiles are available in the market. A tile with side 1 meter costs Rs. 100 and a tile with side 0.5 meters costs Rs. 30. The tiles can be cut if required. What will be the minimum cost of covering the entire floor with tiles?
- (a)
10930
- (b)
10900
- (c)
11000
- (d)
10950
- (e)
10430
Answer: Option A
Text Explanation :
Consider the diagram below:

Area of a 1 × 1 tile = 1 cm2
Total area of A = 9 × 11 = 99 cm2
∴ Number of 1 × 1 tiles required to cover A = 99/1 = 99 tiles.
Total Area of B + C = 9 × 0.5 + 11 × 0.5 = 20 × 0.5 = 10 cm2
∴ Number of 1 × 1 tiles required to cover B and C = 10/1 = 10 tiles.
Now the remaining area i.e., D = 0.5 × 0.5 = 0.25 cm2
It would be better to but a 0.5 × 0.5 tile to cover D.
∴ The minimum cost of covering entire floor with tiles
= (99 + 10) × 100 + 1 × 30 = 10930
Hence, option (a).
Workspace:
A square piece of paper is folded three times along its diagonal to get an isosceles triangle whose equal sides are 10 cm. What is the area of the unfolder original piece of paper?
- (a)
400 sq.cm.
- (b)
800 sq.cm.
- (c)
800√2 sq.cm.
- (d)
1600 sq.cm.
- (e)
Insufficient data to answer
Answer: Option A
Text Explanation :
When a square piece of paper is folded along its diagonal we will get a right isosceles triangle whose area becomes half.
Hence, after 3 such folds we get a right isosceles triangle, whose area is 1/8th the area of the original square.
Area of the folded triangle = ½ × 10 × 10 = 50.
∴ Area of the original square = 8 × 50 = 400 cm2.
Alternately,
If the side of the isosceles triangle is 10 cm then we get the side of the square as 20 cm on unfolding it.
Hence, the area of square = 400 cm2.
Hence, option (a).
Workspace:
The figure below has been obtained by folding a rectangle. The total area of the figure (as visible) is 144 square meters. Had the rectangle not been folded, the current overlapping part would have been a square. What would have been the total area of the original unfolded rectangle?
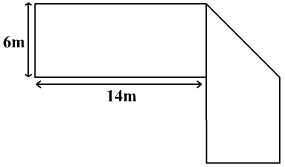
- (a)
128 square meters
- (b)
154 square meters
- (c)
162 square meters
- (d)
172 square meters
- (e)
None of the above
Answer: Option C
Text Explanation :
Had the rectangle not been folded, the overlapping part would have been a square of side 6.
While unfolding, the increase in area
= Area of the triangle =
Area of the given figure = 144 square meters
∴ Area of unfolded rectangle = 144 + 18 = 162 square meters
Hence, option (c).
Workspace:
A solid metal cylinder of 10 cm height and 14 cm diameter is melted and re-cast into two cones in the proportion of 3 : 4 (volume), keeping the height 10 cm. What would be the percentage change in the flat surface area before and after?
- (a)
9%
- (b)
16%
- (c)
25%
- (d)
50%
- (e)
None of the above
Answer: Option D
Text Explanation :
Flat surface area of the cylinder = 2 × π × 72 = 98 π cm2
Volume of the cylinder = π × 72 ×10
= 490 π cm3
Volume of cone A = (3/7) × 490 π = 210 π cm3 = (1/3) × flat surface area of cone
A × 10
Flat surface area of cone A = 63 π cm2
Volume of cone B = (4/7) × 490 π = 280 π cm3 = (1/3) × flat surface area of cone
B × 10
Flat surface area of cone B = 84 π cm2
Total flat surface area of cones
= (63 + 84) π = 147 π cm2
Percentage change in the flat surface area
= (147 – 98)/98 × 100 = 50%
Hence, option (d).
Workspace:
A circular road is constructed outside a square field. The perimeter of the square field is 200 ft. If the width of the road is 7√2 ft. and cost of construction is Rs. 100 per sq. ft. Find the lowest possible cost to construct 50% of the total road.
- (a)
Rs. 70,400
- (b)
Rs. 125,400
- (c)
Rs. 140,800
- (d)
Rs. 235,400
- (e)
None of the above
Answer: Option B
Text Explanation :
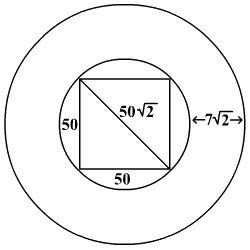
Radius of inner circle = ½ × diagonal of the square = 25√2 cm
Radius of outer circle = Radius of inner circle + width of the road = 32 cm
50% of the area of the road
= 1254 cm2
Cost = 1254 ×100 = Rs. 125,400
Hence, option (b).
Workspace:
Ram, a farmer, managed to grow shaped-watermelons inside glass cases of different shapes. The shapes he used were: a perfect cube, hemi-spherical, cuboid, cylindrical along with the normal spherical shaped watermelons. Thickness of the skin was same for all the shapes. Each of the glass cases was so designed that the total volume and the weight of the all the water-melons would be equal irrespective of the shape.
A customer wants to but water-melons for making juice, for which the skin of the water-melon has to be peeled off, and therefore is a waste. Which shape should the customer buy?
- (a)
Cube
- (b)
Hemi-sphere
- (c)
Cuboid
- (d)
Cylinder
- (e)
Normal spherical
Answer: Option E
Text Explanation :
Let V be the volume of water-melon, S be the total surface area and t be the thickness of the skin, then volume useable for Juice is, V – St
Hence, if total surface area is minimum, then useable volume of the water-melon will be highest.
Now, for equal volume, sphere has the least surface area.
Hence, option (e).
Workspace:
A spherical metal of radius 10 cm is molten and made into 1000 smaller spheres of equal sizes. In this process the surface area of the metal is increased by:
- (a)
1000 times
- (b)
100 times
- (c)
10 times
- (d)
No change
- (e)
None of the above
Answer: Option E
Text Explanation :
Let r be the radius of the smaller sphere.
Now, the volume of the big sphere and the 1000 small spheres is same.
Hence, we have,

Hence, r3 = 1
Hence, r = 1
Now, total surface area of big sphere = 4 × π × 102 = 400π
Total surface area of 1000 new sphere = 1000 × 4π × 12 = 4000π
Hence, total surface area increases by, (4000π – 400π) / 400π = 9 times.
Hence, option (e).
Workspace:
Suresh, who runs a bakery, uses a conical shaped equipment to write decorative labels (e.g., Happy Birthday etc.) using cream. The height of this equipment is 7 cm and the diameter of the base is 5 mm. A full charge of the equipment will write 330 words on an average. How many words can be written using three fifth of a litre of cream?
- (a)
45090
- (b)
45100
- (c)
46000
- (d)
43200
- (e)
None of the above
Answer: Option E
Text Explanation :
Volume of the equipment is;
1/3 × π × r2 × h = 1/3 × 22/7 × 7 × (0.25)2 = 11/6 cm3
Now, 11/24 cm3 can write 330 words.
Hence, 1 cm3 can write,
330 × 24/11 = 720
We know that 1 cm3 = 1 ml
3/5th of a litre is 600 ml which equals 600 cm3
Hence, 600 cm3 will write, 720 × 600 = 432000 words
Hence, option (e).
Workspace:
Carpenter Rajesh has a circular piece of plywood of diameter 30 feet. He has cut out two disks of diameter 20 feet and 10 feet. What is the diameter of the largest disk that can be cut out from the remaining portion of the plywood piece?
- (a)
>8.00 feet and ≤ 8.20 feet
- (b)
> 8.21 feet and ≤ 8.40 feet
- (c)
> 8.41 feet and ≤ 8.60 feet
- (d)
> 8.61 feet and ≤ 8.80 feet
- (e)
> 8.81 feet and ≤ 9.00 feet
Answer: Option C
Text Explanation :
Consider the given diagram,

Here, O is the center of the largest circle, A and B are the centers of the circle having radius 10 and 5 feet respectively.
Let C be the center of the largest circle that can be cut from the remaining portion.
The circles having radius 10 and 5 cm touch each other at point D.
Let radius of the largest circle that can be cut from the remaining portion be r.
Now, one can easily observe that AO = OD = BD = 5 cm.
Now, AC = 10 + r, and BC = 5 + r, and OC = 15 – r
Let DC = a.
Now, applying Apollonius in triangle ADC, we have,
(10 + r)2 + a2 = 2((15 – r)2 + 52)
i.e., a2 – r2 + 80r = 400 … (I)
Similarly, applying Apollonius theorem in triangle OCB, we get,
(15 – r)2 + (5 + r)2 = 2(a2 + 52)
i.e. 2a2 – 2r2 + 20r = 200 … (II)
By, 2 × (I) – (II), we get,
140r = 600
Hence, r = 30/7
Hence, diameter of the required circle = 60/7 ≈ 8.57
Hence, option 3.
Workspace:
A property dealer bought a rectangular piece of land at Rs. 1000/sq. ft. The length of the plot is less than twice its breadth. Due to its size, there were no buyers for the full plot. Hence he decided to sell it in smaller sized pieces as given below.
The largest square from one end was sold at Rs. 1200/sq. ft. From the remaining rectangle the largest square was sold at Rs. 1150/sq. ft.
Due to crash in the property prices, the dealer found it difficult to make profit from the sale of the remaining part of the land. If the ratio of the perimeter of the remaining land to the perimeter of the original land is 3 : 8, at what price (in Rs.) the remaining part of the land is to be sold such that the dealer makes an overall profit of 10%?
- (a)
500/sq. ft.
- (b)
550/sq. ft.
- (c)
600/sq. ft.
- (d)
650/sq. ft.
- (e)
None of the above.
Answer: Option B
Text Explanation :
Consider the following diagram.

Here, a is the length of the plot and b is the height of the plot.
Hence, from the diagram, perimeter of the remaining portion is;
2 × (2b – a + a – b) = 2b
Perimeter of the original land = 2(a + b)
Hence, we have, 2b : 2(a + b) = 3 : 8
Hence, b : a = 3 : 5
Now, without loss of generality we can assume that a = 5 and b = 3
Hence, area of the land = 15 square unit.
Hence, cost of the land = 1000 × 15
Now, selling price of small and big squares are, 9 × 1200 and 4 × 1150 respectively.
Let he sells the remaining land at Rs. x/sq. ft.
Hence, we have,
9 × 1200 + 4 × 1150 + x × 2 = 1100 × 15
Hence, x = 550
Hence, option (b).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report