Geometry - Coordinate Geometry - Previous Year CAT/MBA Questions
The best way to prepare for Geometry - Coordinate Geometry is by going through the previous year Geometry - Coordinate Geometry CAT questions. Here we bring you all previous year Geometry - Coordinate Geometry CAT questions along with detailed solutions.
Click here for previous year questions of other topics.
It would be best if you clear your concepts before you practice previous year Geometry - Coordinate Geometry CAT questions.
In the XY-plane, the area, in sq. units, of the region defined by the inequalities
y ≥ x + 4 and -4 ≤ x2 + y2 + 4(x - y) ≤ 0 is
- (a)
2π
- (b)
π
- (c)
4π
- (d)
3π
Answer: Option A
Text Explanation :
Workspace:
The coordinates of the three vertices of a triangle are: (1, 2), (7, 2), and (1, 10). Then the radius of the incircle of the triangle is
Answer: 2
Text Explanation :
Workspace:
Let C be the circle x2 + y2 + 4x - 6y - 3 = 0 and L be the locus of the point of intersection of a pair of tangents to C with the angle between the two tangents equal to 60 degree. Then, the point at which L touches the line x = 6 is?
- (a)
(6, 6)
- (b)
(6, 8)
- (c)
(6, 3)
- (d)
(6, 4)
Answer: Option C
Text Explanation :
Let C be the circle x2 + y2 + 4x - 6y - 3 = 0 and L be the locus of the point of intersection of a pair of tangents to C with the angle between the two tangents equal to 60 degree. Then, the point at which L touches the line x = 6 is?
Given, x2 + y2 + 4x - 6y - 3 = 0
⇒ x2 + 4x + 4 + y2 - 6y + 9 - 3 - 4 - 9 = 0 [Adding and Subtracting 4 and 9]
⇒ (x + 2)2 + (y - 3)2 = 16
⇒ (x + 2)2 + (y - 3)2 = 42
This represents the equation of a circle with radius = 4 units and center (O) at (-2, 3).
Point L lies on line x = 6, hence x-coordinate of L is 6. Let y-coordinate of L be 'y'.
Let P be the point where tangent from L touches the given circle.
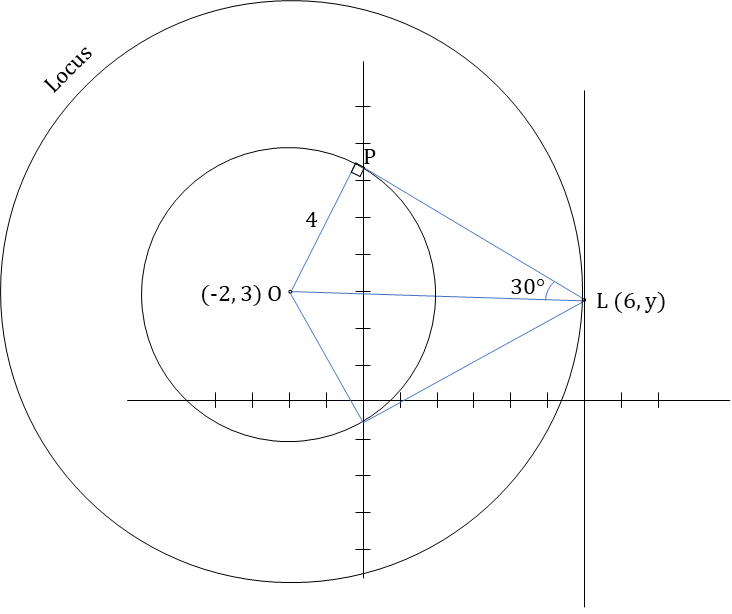
∆LOP is a 30-60-90° triangle.
⇒ OL = 2 × OP = 8
∴ OL = 8 =
⇒ 64 = (8)2 + (3 - y)2
⇒ y = 3
∴ Coordinate of L = (6, 3)
Hence, option (c).
Note: A locus of points is a set of points that all satisfy some given condition or property.
Here L is the locus of the point of intersection of a pair of tangents to C with the angle between the two tangents equal to 60 degree. Hence, L will be a circle bigger than the original circle as shown. Tangents drawn from any point on this circle to the smaller circle will make an angle of 60 degree.
Concept:
Workspace:
The area of the quadrilateral bounded by the Y-axis, the line x = 5 and the lines |x - y| - |5 - x| = 2, is
Answer: 45
Text Explanation :
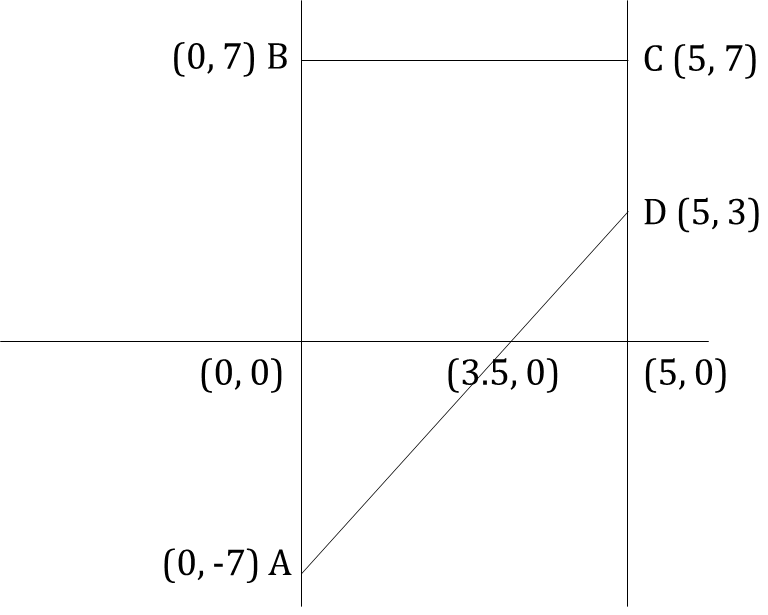
The area of given figure ABCD = 1/2 × (14 + 4) × 5 = 45.
Hence, 45.
Workspace:
Let ABCD be a parallelogram such that the coordinates of its three vertices A, B, C are (1, 1), (3, 4) and (−2, 8), respectively. Then, the coordinates of the vertex D are
- (a)
(4, 5)
- (b)
(0, 11)
- (c)
(-4, 5)
- (d)
(-3, 4)
Answer: Option C
Text Explanation :
Let (x, y) be the coordinates of 4th vertex.
In a parallelogram, diagonals bisect each other.
∴ Intersection point of diagonals is same as the mid-point of two opposite vertices.
Sum of coordinates of two pair of opposite vertices is same.
A and C are opposite vertices while B and D are opposite vertices.
(1, 1) is opposite (-2, 8) while (3, 4) is opposite (x, y)
⇒ 1 - 2 = 3 + x ⇒ x = -4
⇒ 1 + 8 = 4 + y ⇒ y = 5
∴ (x, y) = (-4, 5)
Of the three possibilities only (-4, 5) is mentioned in options.
Hence, option (c).
Workspace:
The points (2, 1) and (-3, -4) are opposite vertices of a parallelogram. If the other two vertices lie on the line x + 9y + c = 0, then c is
- (a)
15
- (b)
12
- (c)
13
- (d)
14
Answer: Option D
Text Explanation :
One of the diagonals of the parallelogram connects the points (2, 1) and (-3, -4).
Line x + 9y + c = 0, represents the other diagonal of the parallelogram.
We know, diagonals of a parallelogram bisect each other.
∴ x + 9y + c = 0 should pass through the midpoint of the line joining (2, 1) and (-3, -4).
The midpoint of the line joining (2, 1) and (-3, -4) = = (-0.5, -1.5)
⇒ Point (-0.5 , -1.5) lies on x + 9y + c = 0.
⇒ -0.5 + 9 × (-1.5) + c = 0
⇒ -0.5 - 13.5 + c = 0
⇒ c = 14.
Hence, option (d).
Workspace:
The vertices of a triangle are (0, 0), (4, 0) and (3, 9). The area of the circle passing through these three points is
- (a)
123π/7
- (b)
205π/9
- (c)
14π/3
- (d)
12π/5
Answer: Option B
Text Explanation :
The diagram can be drawn as follows:

Height of the given triangle = 9 and base = 4
∴ Area of the triangle = = 18
We know area of a triangle = abc/4R
(where a, b, and c are the sides of the triangle and R is the circumradius)
a = AB = 4 units
b = BC = units
c = AC = units
The sides of the triangle are 4, √82 and √90
⇒ 18 =
⇒ R =
∴ Area of the circumcircle = πR2 =
Hence, option (b).
Workspace:
The area, in sq. units, enclosed by the lines x = 2, y = |x – 2| + 4, the X-axis and the Y-axis is equal to
- (a)
6
- (b)
10
- (c)
8
- (d)
12
Answer: Option B
Text Explanation :
We can plot x = 2 and y = |x - 2| + 4
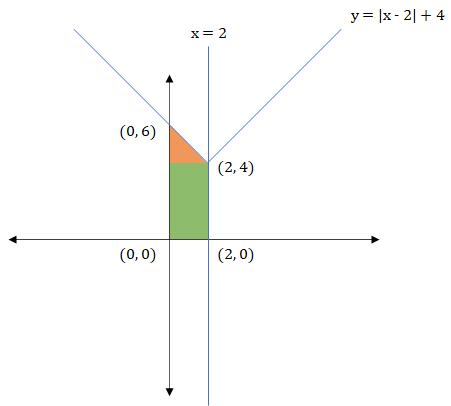
The required area is sum of the triangle (orange) + rectangle (green).
Area of triangle (orange) = 1/2 × 2 × 2 = 2
Area of rectangle = 2 × 4 = 8
∴ Total required area = 2 + 8 = 10 sq. units.
Hence, option (b).
Workspace:
Let S be the set of all points (x, y) in the x-y plane such that |x| + |y| ≤ 2 and |x| ≥ 1. Then, the area, in square units, of the region represented by S equals
Answer: 2
Text Explanation :
|x| ≥ 1 ⇒ x ≥ 1 and x ≤ −1. This is represented as the shaded region in the figure below.

|x| + |y| ≤ 2 : This will have four subcases depending on which quadrant the point is.
1st quadrant (x > 0; y > 0) : y ≤ 2 − x
2nd quadrant (x < 0; y > 0) : y ≤ 2 + x
3rd quadrant (x < 0; y < 0) : y ≥ −2 − x
4th quadrant (x > 0; y < 0) : y ≥ x − 2

Combining these four, the graph for |x| + |y| ≤ 2 is as shown below.

The intersection of |x| + |y| ≤ 2 and |x| ≥ 1 is as shown as the shaded area in the following image.
We need to find Area ∆ABC + Area ∆DEF
Area ∆ABC = Area ∆DEF = (1/2) × BC × AM = (1/2) × 2 × 1 = 1 square unit.
Required area = 1 + 1 = 2 square units.
Hence, 2.
Workspace:
Let T be the triangle formed by the straight line 3x + 5y − 45 = 0 and the coordinate axes. Let the circumcircle of T have radius of length L, measured in the same unit as the coordinate axes. Then, the integer closest to L is
Answer: 9
Text Explanation :
3x + 5y − 45 = 0 cuts the coordinate axes at C(15,0) and A(0,9) as shown in the image below.

∠ABC = 90°, so we can deduce that AC is the diameter of the circumcircle.
[In a right triangle, hypotenuese is the diameter of circumcircle.]
Diameter = √(152 + 92) = √306.
Radius = (√306)/2 = 8.74 ≈ 9 units.
Hence, 9.
Workspace:
A triangle ABC has area 32 sq units and its side BC, of length 8 units, lies on the line x = 4. Then the shortest possible distance between A and the point (0, 0) is
- (a)
8 units
- (b)
4 units
- (c)
2√2 units
- (d)
2√4 units
Answer: Option B
Text Explanation :
The area of the triangle is 32 sq units.
Therefore, 32 = ½ × BC × height
Given, BC = 8
⇒ Height = = 8 cm
Therefore Height of the triangle = 8 cm.
Side BC lies on the line x = 4 or it is parallel to y-axis. Therefore the height of the triangle will be parallel to x axis. In order to minimize the distance of point A from the origin, point A should lie on the x-axis as shown.
Hence, point A is at a distance of 8 units from x = 4 and lies on x-axis.

Therefore point A is (-4,0) and the distance of point A from the origin = 4 units.
Hence, option (b).
Workspace:
The area of the closed region bounded by the equation | x | + | y | = 2 in the two-dimensional plane is
- (a)
4π
- (b)
4
- (c)
8
- (d)
2π
Answer: Option C
Text Explanation :

The closed region bounded by |ax| + |by| = c in the two-dimensional plane has x-intercepts of ± and y-intercepts of ± . This is in general a rhombus. In the given question, we have a square which has each of its diagonals as 4.
Area = 1/2 × 4 × 4 = 8.
Hence, option (c).
Workspace:
The points (2, 5) and (6, 3) are two end points of a diagonal of a rectangle. If the other diagonal has the equation y = 3x + c, then c is
- (a)
-5
- (b)
-6
- (c)
-7
- (d)
-8
Answer: Option D
Text Explanation :
Let ABCD be the rectangle where A = (2, 5) and C= (6, 3).
We know that AC and BD will be the diagonals of the rectangle. It can be represented using the diagram shown below
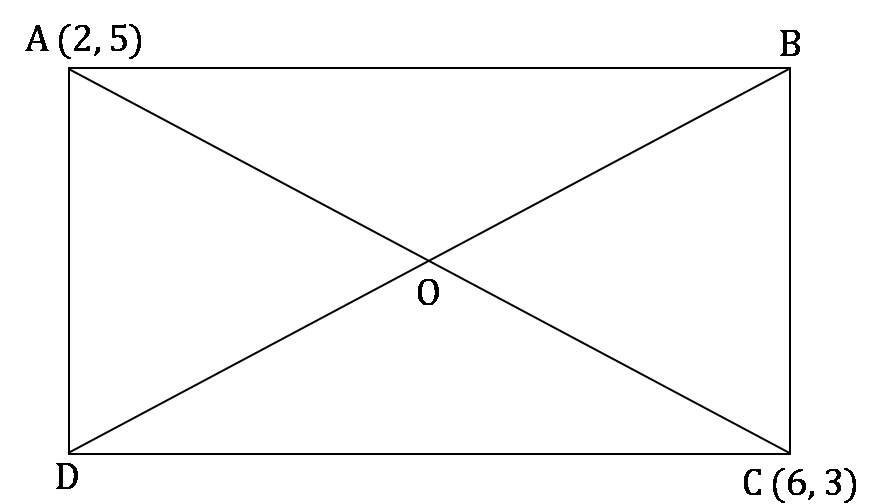
In the above figure, O is the point of intersection of the 2 diagonals and the mid point of both the diagonals.
Mid Point of AC = (4, 4)
Now O also lies on diagonal BD [Diagonal of a rectangle bisect each other.]
Hence co-ordinates of O will satisfy the equation
y = 3x + c
∴ 4 = 3 × 4 + c
⇒ c = – 8
Hence, option (d).
Workspace:
Consider a triangle drawn on the X-Y plane with its three vertices at (41, 0), (0, 41) and (0, 0), each vertex being represented by its (X, Y) coordinates. The number of points with integer coordinates inside the triangle (excluding all the points on the boundary) is
- (a)
780
- (b)
800
- (c)
820
- (d)
741
Answer: Option A
Text Explanation :
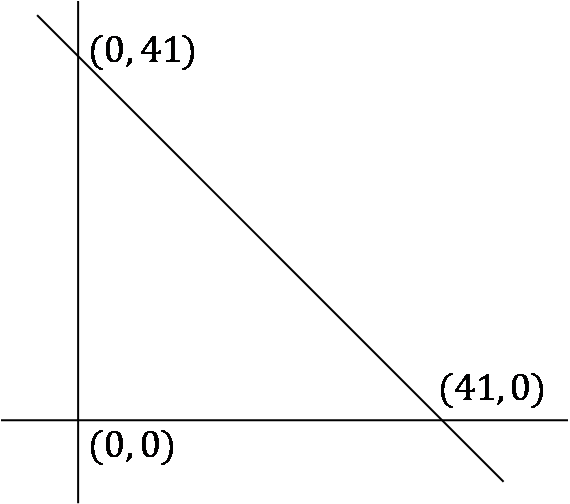
The points satisfying the equations x + y < 41, y > 0, x > 0 lie inside the triangle.
Integer solutions of x + y < 41 can be found as follows:
If x + y = 40, then
(x, y) could be (1, 39), (2, 38), …, (39, 1) ... (39 solutions)
If x + y = 39, then
(x, y) could be (1, 38), (2, 37), …, (38, 1) ... ( 38 solutions)
If x + y = 38, we get 37 solutions and so on till x + y = 2 ... (1 solution)
∴ Total solutions = 1 + 2 + 3 + ... + 39 = 39 × 40/2 = 780 integer solutions to x + y < 41.
The number of points with integer coordinates lying inside the circle = 780
Hence, option (a).
Workspace:
The area of the triangle with the vertices (a, a), (a + 1, a) and (a, a + 2) is
- (a)
a3
- (b)
1
- (c)
0
- (d)
None of these
Answer: Option B
Text Explanation :
Area (∆) =
where x1 = y1 = a, x2 = a + 1, y2 = a, x3 = a and y3 = a + 2
∴ Area (∆) =
∴ Area (∆) = {a[a(1) - (a + 2)(1)] - a[(a + 1)(1) - a(1)] + 1[(a + 1)(a + 2) - a2]} = {- 2a - a + 3a + 2} = 1
Hence, option (b).
Workspace:
The area bounded by the three curves |x + y| = 1, |x| = 1, and |y| = 1, is equal to
- (a)
4
- (b)
3
- (c)
2
- (d)
1
Answer: Option B
Text Explanation :
We need to find area bounded by |x + y| = 1, |x| = 1, and |y| = 1
i.e. all points P(x, y) in the plane such that −1≤ x + y ≤ 1, −1≤ x ≤ 1, and −1≤ y ≤ 1
−1≤ x + y will be the origin side of line x + y = −1
x + y ≤ 1 will be the origin side of line x + y = 1
−1≤ x ≤ 1 will be the area between the lines x = −1 and x = 1.
−1≤ y ≤ 1 will be the area between the lines y = −1 and y = 1.
Tracing these curves, we get the area shown in the graph below

∴ Shaded Area = Area of 3 squares of side 1 unit = 3 × (1)2 = 3
Hence, option (b).
Workspace:
Choose 1; if the question can be answered by using one of the statements alone, but cannot be answered using the other statement alone.
Choose 2; if the question can be answered by using either statement alone.
Choose 3; if the question can be answered by using both statements together, but cannot be answered using either statement alone.
Choose 4; if the question cannot be answered even by using both statements together.
There are two straight lines in the x-y plane with equations ax + by = c , dx + ey = f. Do the two straight lines intersect?
- a, b, c, d, e and f are distinct real numbers.
- c and f are non-zero.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option D
Text Explanation :
Statement A implies that a, b, c, d, e, f are distinct real numbers.
But if a/d = b/e = c/f then the lines may be parallel and might not intersect at all.
∴ Statement A alone is not sufficient.
Statement B implies that the equations are not homogenous equations.
∴ Statement B is also not sufficient.
The condition for intersecting lines is a/d ≠ b/e
Even after combining both the statements the above condition is not clear.
∴ We cannot be sure whether the lines are intersecting or parallel.
Hence, option (d).
Workspace:
Directions: Answer the questions based on the following information.
A robot moves on a graph sheet with X and Y-axis. The robot is moved by feeding it with a sequence of instructions. The different instructions that can be used in moving it, and their meanings are:

The robot reaches point (6, 6) when a sequence of three instructions is executed, the first of which is a GOTO(x,y) instruction, the second is WALKX(2) and the third is WALKY(4). What are the value of x and y?
- (a)
2, 4
- (b)
0, 0
- (c)
4, 2
- (d)
2, 2
Answer: Option C
Text Explanation :
The final point is (6, 6). The previous point is (6, 2) and the one before is (4, 2).
Workspace:
The robot is initially at (x, y), x > 0 and y < 0. The minimum number of instructions needed to be executed to bring it to the origin (0, 0) if you are prohibited from using the GOTO instruction is
- (a)
2
- (b)
1
- (c)
x + y
- (d)
0
Answer: Option A
Text Explanation :
Two instructions are needed, one parallel to the X-axis and the other parallel to the Y-axis. i.e. WALKX(–x) and WALKY (–y)
Workspace:
What is the distance between the points A(3, 8) and B(–2, –7)?
- (a)
5√2
- (b)
5
- (c)
5√10
- (d)
10√2
Answer: Option A
Text Explanation :
The distance between two points (x1, y1) and (x2, y2) is given as
Hence, required distance = = 5√10.
Hence, option (c).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report