Geometry - Triangles - Previous Year CAT/MBA Questions
The best way to prepare for Geometry - Triangles is by going through the previous year Geometry - Triangles CAT questions. Here we bring you all previous year Geometry - Triangles CAT questions along with detailed solutions.
Click here for previous year questions of other topics.
It would be best if you clear your concepts before you practice previous year Geometry - Triangles CAT questions.
ABCD is a rectangle with sides AB = 56 cm and BC = 45 cm, and E is the midpoint of side CD. Then, the length, in cm, of radius of incircle of ∆ADE is
Answer: 10
Text Explanation :
Workspace:
The midpoints of sides AB, BC, and AC in ∆ABC are M, N, and P, respectively. The medians drawn from A, B, and C intersect the line segments MP, MN and NP at X, Y, and Z, respectively. If the area of ∆ABC is 1440 sq cm, then the area, in sq cm, of ∆XYZ is
Answer: 90
Text Explanation :
Workspace:
In a right-angled triangle ∆ABC, the altitude AB is 5 cm, and the base BC is 12 cm. P and Q are two points on BC such that the areas of ∆ABP, ∆ABQ and ∆ABC are in arithmetic progression. If the area of ∆ABC is 1.5 times the area of ∆ABP, the length of PQ, in cm, is
Answer: 2
Text Explanation :
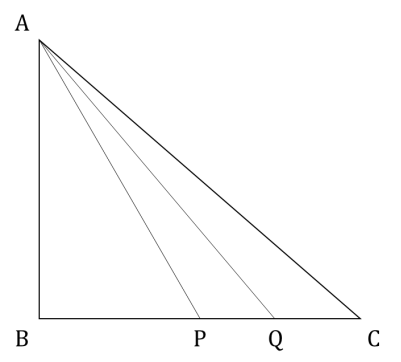
Given, AB = 5 and BC = 12
Area of ∆ABP = ½ × AB × BP = 2.5 × BP …(1)
Area of ∆ABQ = ½ × AB × BQ = 2.5 × BQ …(2)
Area of ∆ABC = ½ × AB × BC = 2.5 × BC …(3)
Given, (3) = 1.5 × (1)
⇒ 2.5 BC = 1.5 × 2.5 × BP
⇒ BC = 1.5 × BP
⇒ 12 = 1.5 × BP
⇒ BP = 8
Also, Areas of ∆ABP, ∆ABQ and ABC are in arithmetic progression.
⇒ 2 × (2) = (1) + (3)
⇒ 2 × 2.5 × BQ = 2.5 × BP + 2.5 × BC
⇒ 2BQ = BP + BC
⇒ 2BQ = 8 + 12
⇒ BQ = 10
∴ PQ = BQ – BP = 10 – 8 = 2
Hence, 2.
Concept:
Workspace:
A triangle is drawn with its vertices on the circle C such that one of its sides is a diameter of C and the other two sides have their lengths in the ratio a : b. If the radius of the circle is r, then the area of the triangle is
- (a)
- (b)
- (c)
- (d)
Answer: Option A
Text Explanation :
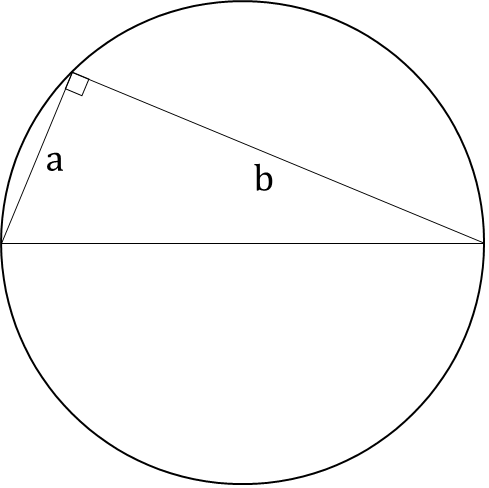
Concept: Diameter of a circle makes an angle of 90° on the circle.
∴ (2r)2 = a2 + b2
⇒ 4r2 = a2 + b2
Now, Area of the triangle = 1/2 × base × height
= 1/2 × a × b
=
=
=
Hence, option (a).
Workspace:
Let triangle ABC be isosceles triangle such that AB and AC are of equal lenght. AD is the altitude from A on BC and BE is the altitude from B on AC. If AD and BE intersect at O such that ∠AOB = 105°, then AD/BE equals?
- (a)
2 cos 15°
- (b)
cos 15°
- (c)
2 sin 15°
- (d)
sin 15°
Answer: Option A
Text Explanation :
In △OBD, ∠OBD = 90 - 75 = 15°
In △EBC, ∠ECB = 90 - 15 = 75°
Similarly, ∠B = 75° and ∠A = 180 - 75 - 75 = 30°
Area of △ABC = =
⇒ = ...(2)
Area of △ABC = =
⇒ = = 2 × Sin 75° = 2 × Cos (90 - 15)° = 2 × Cos 15°
⇒ = = 2 × Cos 15°
Hence, option (a).
Workspace:
In triangle ABC, altitudes AD and BE are drawn to the corresponding bases. If ∠BAC = 45° and ∠ABC = θ, then AD/BE equals
- (a)
1
- (b)
√2 cosθ
- (c)
√2 sinθ
- (d)
(sinθ + cosθ)/√2
Answer: Option C
Text Explanation :
Area of ∆ABC = × AB × AC × sin 45° = ...(1)
Area of ∆ABC = × BA × BC × sin θ° = ...(2)

(1) = (2)
⇒ =
⇒ = √2 × sin𝜃 ...(3)
Area of ∆ABC = × AD × BC = × AC × BE
⇒ =
⇒ = √2 × sin𝜃
Hence, option (c).
Workspace:
The length of each side of an equilateral triangle ABC is 3 cm. Let D be a point on BC such that the area of triangle ADC is half the area of triangle ABD. Then the length of AD, in cm, is
- (a)
√7
- (b)
√6
- (c)
√5
- (d)
√8
Answer: Option A
Text Explanation :
Area of ∆ACD is half of area of ∆ABD.
Since their height is same, ratio of their areas will be same as the ratio of their bases.
⇒ BD = 2CD
⇒ BD = 2 cm and CD = 1 cm.

Taking E as the midpoint of BC, BE = 3/2 = 1.5
⇒ ED = 2 – 1.5 = 0.5 cm.
Also, AE = height of the equilateral triangle = × 3 =

In ∆AED
⇒ AD2 = AE2 + ED2
⇒ AD2 = + (0.5)2
⇒ AD2 = + = 7
⇒ AD =
Hence, option (a).
Workspace:
Two ships are approaching a port along straight routes at constant speeds. Initially, the two ships and the port formed an equilateral triangle with sides of length 24 km. When the slower ship travelled 8 km, the triangle formed by the new positions of the two ships and the port became right-angled. When the faster ship reaches the port, the distance, in km, between the other ship and the port will be
- (a)
6
- (b)
8
- (c)
12
- (d)
4
Answer: Option C
Text Explanation :
Initially both ships are at a distance of 24 kms from the port (A).
Let the distance travelled by faster ship be F kms when slower ship travels 8 kms.

Now, ∆ABC is a right triangle when ∠BAC = 60°
⇒ AC = ½ × AB = 8 kms.
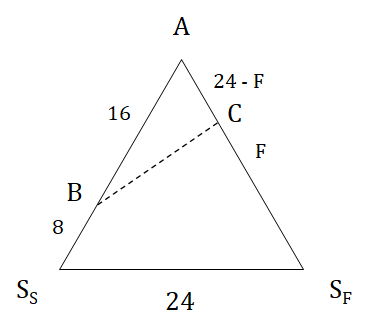
∴ 24 – F = 8
⇒ F = 16 kms
Ratio of speeds of faster and slower ships = 16 : 8 = 2 : 1
Now, when the faster ships reaches port it would have travelled 24 kms and the slower ship would have travelled 12 kms.
∴ Slower ship will be 24 – 12 = 12 kms from the port.
Hence, option (c).
Workspace:
Suppose the medians BD and CE of a triangle ABC intersect at a point O. If area of triangle ABC is 108 sq. cm., then, the area of the triangle EOD, in sq. cm., is
Answer: 9
Text Explanation :
BD, CE and AF are medians of the triangle ABC.

We know centroid (O) divides the triangle in 6 smaller triangles of equal area.
⇒ Area(∆EOB) = Area(∆BOF) = Area(∆FOC) = Area(∆COD) = 1/6 × 108 = 18.
∆AED ~ ∆ABC
⇒ = =
⇒ Area(EBCD) = ¾ × 108 = 81
Now,
Area(∆EOD) = Area(EBCD) – [Area(∆EOB) + Area(∆BOF) + Area(∆FOC) + Area(∆COD)]
= 81 – 72 = 9
Hence, 9.
Workspace:
Let D and E be points on sides AB and AC, respectively, of a triangle ABC, such that AD : BD = 2 : 1 and AE : CE = 2 : 3. If the area of the triangle ADE is 8 sq cm, then the area of the triangle ABC, in sq cm, is
Answer: 30
Text Explanation :
Consider the figure below.
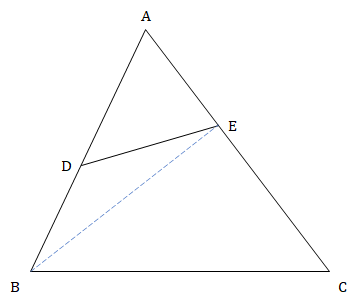
Consider ∆AED and ∆BED.
Height of both triangles is same, hence ratio of area will be same as ratio of their base.
∴ Area(∆AED)/Area(∆BED) = AD/BD = 2/1
Area (∆BED) = 8/2 = 4
∴ Area (∆ABE) = 8 + 4 = 12
Now, consider ∆AED and ∆BED.
Height of both triangles is same, hence ratio of area will be same as ratio of their base.
∴ Area(∆ABE)/Area(∆CBE) = AE/CE = 2/3
Area (∆CBE) = 3/2 × 12 = 18
∴ Area (∆ABC) = 12 + 18 = 30 sq. cm.
Hence, 30.
Workspace:
In a triangle ABC, ∠BCA = 50°. D and E are points on AB and AC, respectively, such that AD = DE. If F is a point on BC such that BD = DF, then ∠FDE, in degrees is equal to
- (a)
96
- (b)
100
- (c)
80
- (d)
72
Answer: Option C
Text Explanation :

In the figure above:
In ∆ABC,
∠A + ∠B + ∠C = 180°
⇒ x + y = 130°
Since DA = DE
⇒ ∠DAE = ∠DEA = x
⇒ ∠ADE = 180° – 2x
Also, DB = DF
⇒ ∠DBF = ∠DFB = y
⇒ ∠BDC = 180° – 2y
∠ADE + ∠EDF + ∠FDB = 180°
⇒ 180 – 2x + ∠EDF + 180 – 2y = 180
⇒ ∠EDF = 2x + 2y – 180
⇒ ∠EDF = 260° – 180° = 80°
Hence, option (c).
Workspace:
From an interior point of an equilateral triangle, perpendiculars are drawn on all three sides. The sum of the lengths of the three perpendiculars is s. Then the area of the triangle is
- (a)
S2/√3
- (b)
√3S2/2
- (c)
S2/2√3
- (d)
2S2/√3
Answer: Option A
Text Explanation :
The figure can be drawn as below.

Sum of areas of three smaller ∆s = Area of ∆ABC
⇒ + + =
⇒ =
⇒ a =
∴ Area of ∆ABC = = =
Hence, option (a).
Workspace:
Corners are cut off from an equilateral triangle T to produce a regular hexagon H. Then, the ratio of the area of H to the area of T is
- (a)
5 : 6
- (b)
4 : 5
- (c)
3 : 4
- (d)
2 : 3
Answer: Option D
Text Explanation :
The hexagon will be regular only if the hexagon is symmetrical with resepect to the original triangle.
This is only possible when the corners cut are all equilateral (of let's say side x) and the side length of the hexagon is equal to side length of the equilateral corner (again x).
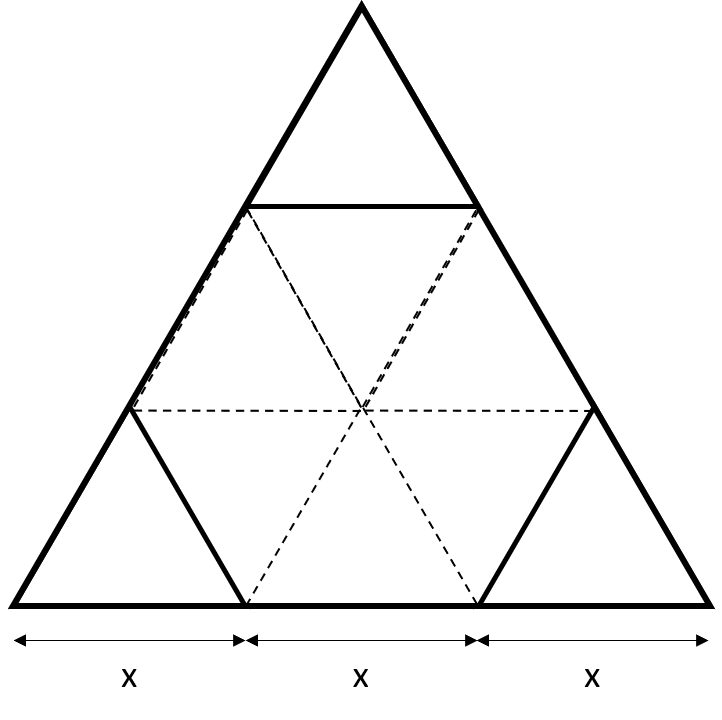
H = 6 × x2 (∵ A regular hexagon consists of six equilateral triangles of side length equal to the side length of the hexagon)
T = (3x)2 = x2 (∵ Side length of the triangle = x + x + x = 3x)
∴ = = .
Hence, option (d).
Workspace:
In a triangle ABC, medians AD and BE are perpendicular to each other, and have lengths 12 cm and 9 cm, respectively. Then, the area of triangle ABC, in sq cm, is
- (a)
80
- (b)
68
- (c)
72
- (d)
78
Answer: Option C
Text Explanation :
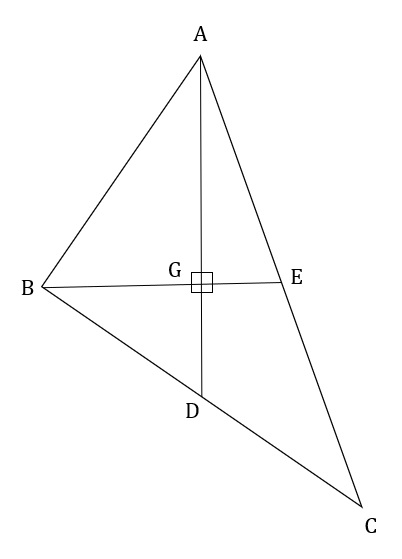
As AD and BE are medians, so G is the centroid of ∆ABC.
So, AG : GD = BG : GE = 2 : 1.
∴ AG = 8 cm, GD = 4 cm, BG = 6 cm and GE = 3 cm.
If we join centroid with all 3 vertices, we get 3 triangles of equal areas.
∴ Area of ∆ABC = 3 × Area of ∆ABG
⇒ Area of ∆ABC = 3 × (1/2 × 8 × 6) = 72 sq. cm.
Hence, option (a).
Workspace:
Let ABC be a right-angled triangle with hypotenuse BC of length 20 cm. If AP is perpendicular on BC, then the maximum possible length of AP, in cm, is
- (a)
10
- (b)
8√2
- (c)
6√2
- (d)
5
Answer: Option A
Text Explanation :
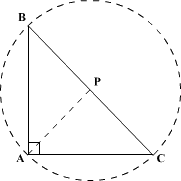
∠BAC = 90°, so BC can be considered diameter of a circle with center anywhere on BC.
AP is maximum when it is the perpendicular bisector from the vertex to the hypotenuse. So, BP = PC = 20/2 = 10. This implies that P is the center of the circle.
∴ AP = BP = PC = 10 cm.
Hence, option (b).
Workspace:
Given an equilateral triangle T1 with side 24 cm, a second triangle T2 is formed by joining the midpoints of the sides of T1. Then a third triangle T3 is formed by joining the midpoints of the sides of T2. If this process of forming triangles is continued, the sum of the areas, in sq cm, of infinitely many such triangles T1, T2, T3,... will be
- (a)
248√3
- (b)
164√3
- (c)
188√3
- (d)
192√3
Answer: Option D
Text Explanation :

Consider ∆ABC (i.e. T1) and ∆DEF (i.e., T2).
D and E are midpoints of AB and AC respectively. Therefore, BC = 2 × DE
Side of T2 = 1/2 × Side of T1
Area of T1 = A(T1) = √3/4 × 242
Similarly, A(T2) = √3/4 × 122
A(T3) = √3/4 × 62 ... and so on
Sum of areas of infinitely many Ti’s
= √3/4 × 242 + √3/4 × 122 + √3/4 × 62 + ...
= √3/4 (242 + 122 + 62 + ...)
Here, (242 + 122 + 62 + ...) is an infinite series with r = 1/4
Hence, = √3/4 (242 + 122 + 62 + ...) = = 192√3
Hence, option (d).
Workspace:
On a triangle ABC, a circle with diameter BC is drawn, intersecting AB and AC at points P and Q, respectively. If the lengths of AB, AC, and CP are 30 cm, 25 cm, and 20 cm respectively, then the length of BQ, in cm, is
Answer: 24
Text Explanation :

Since points P and Q lie on the circumference of the circle drawn with BC as diameter, angles BPC and BQC are right angled triangles.
Now, area of triangle ABC = =
Therefore, BQ = = = 24
Hence, 24.
Workspace:
From a triangle ABC with sides of lengths 40 ft, 25 ft and 35 ft, a triangular portion GBC is cut off where G is the centroid of ABC. The area, in sq ft, of the remaining portion of triangle ABC is:
- (a)
225√3
- (b)
500/√3
- (c)
275√3
- (d)
250√3
Answer: Option B
Text Explanation :
The medians of a triangle divide the triangle into six parts of equal area.
Area of the triangle) = =
Area of GBC = (Area of the triangle)
∴ Area of the remaining portion = 2/3 × 250√3 = 500√3/3 = 500/√3
Hence, option (b).
Workspace:
Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq. cm, of the region enclosed by BPC and BQC is:
- (a)
9π - 18
- (b)
18
- (c)
9π
- (d)
9
Answer: Option B
Text Explanation :
AB = a (a = 6)
BC = a√2
BCQB is a semicircle of radius = half of BC =
Area of semicircle BCQB = ½ × π × = ¼ × π × a2
ACPBA is a quarter circle (quadrant) of radius a.
Area of BCPB = Area of sector ABPCA - Area of triangle ABC
= ¼ × π × a2 - Area of triangle ABC
Now, Area of CPBQC = Area of semicircle CQB - Area of CPBC
= ¼ × π × a2 - ( ¼ × π × a2 - Area of triangle ABC)
= Area of triangle ABC
∴ Area of region enclosed by CPBQC = Area of ∆ABC = ½ × 6 × 6 = 18.
Hence, option (b).
Workspace:
Let ABC be a right-angled triangle with BC as the hypotenuse. Lengths of AB and AC are 15 km and 20 km, respectively. The minimum possible time, in minutes, required to reach the hypotenuse from A at a speed of 30 km per hour is:
Answer: 24
Text Explanation :
Given triangle is right triangle with smaller sides as 15 and 20, hence the hypotenuse will be 25.
Altitude from right vertex to hypotenuse = (15 × 20)/25 = 12
This is the shortest distance from A to BC. At 30 km/hr = 12/30 hrs = 12/30 × 60 mins = 24 mins.
Hence, 24.
Workspace:
Let P be an interior point of a right-angled isosceles triangle ABC with hypotenuse AB. If the perpendicular distance of P from each of AB, BC, and CA is 4(√2 - 1) m, then the area, in sq cm, of the triangle ABC is
Answer: 16
Text Explanation :
Now since the perpendicular distance of P from each 3 sides is the same, it is the incenter of the triangle ABC.
Let ‘x’ be one of the equal sides of the isosceles right angled triangle ABC.
So the length of the hypotenuse will be √2x.
Area of right triangle ABC =
So the Area of triangle ABC can also be expressed as a product of the in radius ‘r’ and semi perimeter ‘s’.
s = = x +
∴ Area = =
⇒ 4√2x - 4x + 4x - 2√2x =
⇒ 2√2x =
⇒ x = 4√2
Area of triangle ABC = ½ × 4√2 × 4√2 = 16 sq.units.
Hence, 16.
Workspace:
In a triangle ABC, the lengths of the sides AB and AC equal 17.5 cm and 9 cm respectively. Let D be a point on the line segment BC such that AD is perpendicular to BC. If AD = 3 cm, then what is the radius (in cm) of the circle circumscribing the triangle ABC?
- (a)
17.05
- (b)
27.85
- (c)
22.45
- (d)
32.25
- (e)
26.25
Answer: Option E
Text Explanation :

We know that the area (A) of triangle (ABC) is related to the circum radius (R) and sides of the triangle as follows:
R =
Where, Area (A) = ½ × AD × BC
∴ R = = = = 26.25 cm
Hence, option (e).
Workspace:
Consider obtuse-angled triangles with sides 8 cm, 15 cm and x cm. If x is an integer, then how many such triangles exist?
- (a)
5
- (b)
21
- (c)
10
- (d)
15
- (e)
14
Answer: Option C
Text Explanation :
We know that for an obtuse triangle of sides a, b and c (where c is the largest side),
a2 + b2 < c2
We also know that for a triangle, a + b > c
Let the third side be x.
These present us with two limiting cases.
Case 1: Let 8 cm and 15 cm be the shorter sides. The value of the largest side (x) must be greater than
Also, x < 8 + 15 = 23.
The possible integer values of x are 18, 19, 20, 21 and 22 cm.
We cannot consider values from 23 onwards because 8 + 15 = 23 and this violates the second condition.
Case 2: Let 8 and x be the shorter sides and 15 cm is the largest side.
The value of the remaining side (x) must be less than
Also, x > 15 - 8 = 7
The possible integer values are 12, 11, 10, 9 and 8 cm.
We cannot consider values less than 8 because 7 + 8 = 15 and this violates the second condition.
Thus, we have 10 possible values for x.
Hence, option (c).
Workspace:
Consider the triangle ABC shown in the following figure where BC = 12 cm, DB = 9 cm, CD = 6 cm and ∠BCD = ∠BAC. What is the ratio of the perimeter of the triangle ADC to that of the triangle BDC?

- (a)
7/9
- (b)
8/9
- (c)
6/9
- (d)
5/9
Answer: Option A
Text Explanation :
m ∠BCD = m ∠BAC and B is common to triangles ABC and CBD.
∆ABC is similar to ∆CBD.
AB/CB = BC/BD = AC/CD
AB/12 = 12/9 = AC/6
AB = 16 cm and AC = 8 cm
AD = AB – BD = 16 – 9 = 7 cm
∴ Perimeter of ∆ADC = 7 + 6 + 8 = 21 cm
∴ Perimeter of ∆BDC = 9 + 6 + 12 = 27 cm
∴ Required ratio = 21/27 = 7/9
Hence, option (a).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
D, E, F are the mid-points of the sides AB, BC and CA of triangle ABC respectively. What is the area of DEF in square centimetres?
A. AD = 1 cm, DF = 1 cm and perimeter of DEF = 3 cm
B. Perimeter of ABC = 6 cm, AB = 2 cm, and AC = 2 cm
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option B
Text Explanation :
D, E and F are the midpoints of AB, BC and CA respectively.
Using statement A alone:
∵ AD = 1 cm
∴ BD = 1 cm …(Since D is the mid-point)
∵ DF = 1 cm
∴ BC = 2 cm …(Since D and F are the mid-points and DF is parallel to BC)
∴ BE = 1 cm and EC = 1 cm
∵ Perimeter of DEF = 3 cm
∴ EF = 1 cm
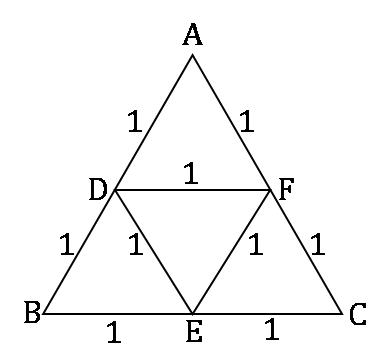
∴ Area of ∆DEF can be obtained.
So, statement A alone is sufficient to obtain the answer.
Using statement B alone:
∵ Perimeter of ∆ABC = 6 cm, AB = 2 cm, AC = 2 cm
∴ BC = 2 cm
∴ DE = 1, EF = 1 and DF = 1

So, statement B alone is also sufficient to obtain the answer.
Hence, option (b).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report