Modern Math - Permutation & Combination - Previous Year CAT/MBA Questions
The best way to prepare for Modern Math - Permutation & Combination is by going through the previous year Modern Math - Permutation & Combination CAT questions. Here we bring you all previous year Modern Math - Permutation & Combination CAT questions along with detailed solutions.
Click here for previous year questions of other topics.
It would be best if you clear your concepts before you practice previous year Modern Math - Permutation & Combination CAT questions.
P, Q, R and S are four towns. One can travel between P and Q along 3 direct paths, between Q and S along 4 direct paths, and between P and R along 4 direct paths. There is no direct path between P and S, while there are few direct paths between Q and R, and between R and S. One can travel from P to S either via Q, or via R, or via Q followed by R, respectively, in exactly 62 possible ways. One can also travel from Q to R either directly, or via P, or via S, in exactly 27 possible ways. Then, the number of direct paths between Q and R is
Answer: 7
Text Explanation :
Workspace:
The number of all positive integers up to 500 with non-repeating digits is
Answer: 378
Text Explanation :
Workspace:
After two successive increments, Gopal's salary became 187.5% of his initial salary. If the percentage of salary increase in the second increment was twice of that in the first increment, then the percentage of salary increase in the first increment was
- (a)
30
- (b)
25
- (c)
27.5
- (d)
20
Answer: Option B
Text Explanation :
Workspace:
The number of all natural numbers up to 1000 with non-repeating digits is:
- (a)
648
- (b)
585
- (c)
738
- (d)
504
Answer: Option C
Text Explanation :
Single-digit such numbers = 9
2-digit such numbers: __ __
Ten’s digit can be filled in 9 ways (i.e., 1, 2, 3, …, 9)
Unit’s digit can be filled in 9 ways (i.e., any of the 10 single digits except the one at ten’s place)
⇒ Total such 2-digit numbers = 9 × 9 = 81
3-digit such numbers: __ __ __
Hundred’s digit can be filled in 9 ways (i.e., 1, 2, 3, …, 9)
Ten’s digit can be filled in 9 ways (i.e., any of the 10 single digits except the one at hundred’s place)
Unit’s digit can be filled in 8 ways (i.e., any of the 10 single digits except the ones at hundred’s and ten’s place)
⇒ Total such 3-digit numbers = 9 × 9 × 8 = 648
∴ Total such numbers = 9 + 81 + 648 = 738.
Hence, option (c).
Workspace:
The number of ways of distributing 20 identical balloons among 4 children such that each child gets some balloons but no child gets an odd number of balloons, is
Answer: 84
Text Explanation :
Let the number of balloons each child gets is 2a, 2b, 2c and 2d respectively.
a, b, c, d > 0
⇒ 2a + 2b + 2c + 2d = 20
⇒ a + b + c + d = 10
Number of combinations of a, b, c and d such that a, b, c and d > 0 = (10-4)+4-1C4-1 = 9C3 = 84.
Hence, 84.
Workspace:
The number of integers greater than 2000 that can be formed with the digits 0, 1, 2, 3, 4, 5, using each digit at most once, is
- (a)
1200
- (b)
1420
- (c)
1440
- (d)
1480
Answer: Option C
Text Explanation :
Case 1: Number of 4-digit numbers
__ __ __ __
Here,
unit’s digit can be either 2, 3, 4 or 5 i.e., 4 ways,
ten’s digit can be chosen from remaining 5 numbers in 5 ways,
hundred’s digit can be chosen from remaining 4 numbers in 4 ways.
thousand’s digit can be chosen from remaining 3 numbers in 3 ways.
⇒ Total such 4-digit numbers = 4 × 5 × 4 × 3 = 240
Case 2: Number of 5-digit numbers
__ __ __ __ __
Here,
unit’s digit can be either 1, 2, 3, 4 or 5 i.e., 5 ways,
ten’s digit can be chosen from remaining 5 numbers in 5 ways,
hundred’s digit can be chosen from remaining 4 numbers in 4 ways.
thousand’s digit can be chosen from remaining 3 numbers in 3 ways.
ten thousand’s digit can be chosen from remaining 2 numbers in 2 ways.
⇒ Total such 5-digit numbers = 5 × 5 × 4 × 3 × 2 = 600
Case 2: Number of 6-digit numbers
__ __ __ __ __
Here,
unit’s digit can be either 1, 2, 3, 4 or 5 i.e., 5 ways,
ten’s digit can be chosen from remaining 5 numbers in 5 ways,
hundred’s digit can be chosen from remaining 4 numbers in 4 ways.
thousand’s digit can be chosen from remaining 3 numbers in 3 ways.
ten thousand’s digit can be chosen from remaining 1 number in 1 way.
One lakh’s digit
⇒ Total such 6-digit numbers = 5 × 5 × 4 × 3 × 2 × 1 = 600
∴ Total required numbers = 240 + 600 + 600 = 1440.
Hence, option (c).
Workspace:
The arithmetic mean of all the distinct numbers that can be obtained by rearranging the digits in 1421, including itself, is
- (a)
2222
- (b)
2592
- (c)
2442
- (d)
3333
Answer: Option A
Text Explanation :
8. Let us consider the sum of unit’s digit of all such numbers.
__ __ __ x
If 1 occupies the units digit, number of such numbers = 3! = 6
Sum of all the units digit of such numbers = 6 × 1 = 6
If 2 occupies the units digit, number of such numbers = 3!/2! = 3
Sum of all the units digit of such numbers = 3 × 2 = 6
If 4 occupies the units digit, number of such numbers = 3!/2! = 3
Sum of all the units digit of such numbers = 3 × 4 = 12
∴ Sum of unit’s digits of all possible numbers = 6 + 6 + 12 = 24
Similarly,
Sum of ten’s digits of all possible numbers = 24 × 10 = 240
Sum of hundred’s digits of all possible numbers = 24 × 100 = 2400
Sum of thousand’s digits of all possible numbers = 24 × 1000 = 24000
⇒ Sum of all such numbers = 24 + 240 + 2400 + 24000 = 26664
Also, number of such numbers = 4!/2! = 12
∴ Average of all such numbers = 2664/12 = 2222
Hence, option (a).
Workspace:
The number of groups of three or more distinct numbers that can be chosen from 1, 2, 3, 4, 5, 6, 7 and 8 so that the groups always include 3 and 5, while 7 and 8 are never included together is
Answer: 47
Text Explanation :
Out of the seven integers given, 3 and 5 should always be selected.
Case 1: Exactly 1 of 7 or 8 is selected.
Exactly one of 7 or 8 can be selected in 2 ways.
Now we have already selected three integers.
For each of the remaining 4 integers, it may be selected or it may not be selected.
∴ Number of ways of selection for remaining integers = 2 × 2 × 2 × 2 = 16
∴ Total number of ways = 2 × 16 = 32
Case 2: None of 7 and 8 is selected.
So far we have selected only two integer.
For each of the remaining 4 integers, it may be selected or it may not be selected.
∴ Number of ways of selection for remaining integers = 2 × 2 × 2 × 2 = 16
But this includes one way when no integer is selected.
∴ Number of ways of selecting at least one integer = 16 – 1 = 15
∴ Total number of ways = 32 + 15 = 47.
Hence, 47.
Workspace:
The number of ways of distributing 15 identical balloons, 6 identical pencils and 3 identical erasers among 3 children, such that each child gets at least four balloons and one pencil, is
Answer: 1000
Text Explanation :
We know that number of distributing n identical objects amongst r different groups = n+r-1Cr-1
Distributing balloons
Since each child gets at least 4 balloons, we will first give 4 balloons to each of the 3 children.
Now we have 3 identical balloons to be distributed to 3 children.
Number of ways of doing this = 3+3-1C3-1 = 10 ways
Distributing pencils
Since each child gets at least 1 pencil, we will first give 1 pencil to each of the 3 children.
Now we have 3 identical pencils to be distributed to 3 children.
Number of ways of doing this = 3+3-1C3-1 = 10 ways
Distributing erasers
We have 3 identical erasers to be distributed to 3 children.
Number of ways of doing this = 3+3-1C3-1 = 10 ways
∴ Total number of ways = 10 × 10 × 10 = 1000
Hence, 1000.
Workspace:
A four-digit number is formed by using only the digits 1, 2 and 3 such that both 2 and 3 appear at least once. The number of all such four-digit numbers is
Answer: 50
Text Explanation :
Case 1: Number contains 2, 3, 1, 1
Number of such numbers = 4!/2! = 12
Case 2: Number contains 2, 3, 3, 1
Number of such numbers = 4!/2! = 12
Case 3: Number contains 2, 2, 3, 1
Number of such numbers = 4!/2! = 12
Case 4: Number contains 2, 2, 3, 3
Number of such numbers = 4!/(2!×2!) = 6
Case 5: Number contains 2, 2, 2, 3
Number of such numbers = 4!/3! = 4
Case 6: Number contains 2, 3, 3, 3
Number of such numbers = 4!/3! = 4
∴Total such numbers = 12 + 12 + 12 + 6 + 4 + 4 = 50.
Hence, 50.
Workspace:
How many 4-digit numbers, each greater than 1000 and each having all four digits distinct, are there with 7 coming before 3?
Answer: 315
Text Explanation :
Out of 4 digits we already have 7 and 3. Now we have to select 2 more digits.
Case 1: zero is not selected.
We can select 2 more digits out of 7 in 7C2 = 21 ways.
These 4 digits can be arranged in 4! = 24 ways
∴ Total number of ways = 21 × 24 = 504 ways.
Now, in half of these numbers 7 would be before 3 and in other half 3 would be before 7.
∴ 7 comes before 3 in 504/2 = 252 ways.
Case 2: zero is selected.
We can select 1 more digit out of 7 in 7C1 = 7 ways.
These 4 digits can be arranged in 3 × 3! = 18 ways
∴ Total number of ways = 7 × 18 = 126 ways.
Now, in half of these numbers 7 would be before 3 and in other half 3 would be before 7.
∴ 7 comes before 3 in 126/2 = 63 ways.
∴ Total numbers in which 7 comes before 3 = 252 + 63 = 315.
Hence, 315.
Workspace:
How many integers in the set {100, 101, 102, ..., 999} have at least one digit repeated?
Answer: 252
Text Explanation :
Here we have to find all 3-digit numbers which have at least one digit repeated.
This can also be calculated by subtracting all 3-digit number which do not have any repeated digits from total 3-digit numbers.
Total 3-digit numbers = 9 × 10 × 10 = 900
3-digit numbers without repetition,

∴ The number 3-digit numbers without repetition = 9 × 9 × 8 = 648
Therefore, the number of 3-digit numbers which have at least one digit repeated 900 – 648 = 252.
Hence, 252.
Workspace:
With rectangular axes of coordinates, the number of paths from (1, 1) to (8, 10) via (4, 6), where each step from any point (x, y) is either to (x, y + 1) or to (x + 1, y), is
Answer: 3920
Text Explanation :
We have to go from (1, 1) to (8, 10) via (4, 6)
Number of paths from (1,1) to (8,10) = [Number of paths from (1,1) to (4,6)] × [Number of paths from (4,6) to (8,10)]
Path from (1,1) to (4,6):
Number of horizontal displacements (∆x) = 4 − 1 = 3 units and
Number of vertical displacements (∆y) = 6 − 1 = 5 units.
Hence, a total of 8 units.
∴ Number of paths from (1,1) to (4,6) = 8C3 × 5C5 = 56.
Path from (4,6) to (8,10):
Number of horizontal displacements (∆x) = 8 − 4 = 4 units and
Number of vertical displacements (∆y) = 10 − 6 = 4 units.
Hence, a total of 8 units.
∴ Number of paths from (4,6) to (8,10) = 8C4 × 4C4 = 70.
Total required number of paths = 56 × 70 = 3920.
Hence, 3920.
Workspace:
How many numbers with two or more digits can be formed with the digits 1, 2, 3, 4, 5, 6, 7, 8, 9, so that in every such number, each digit is used at most once and the digits appear in the ascending order?
Answer: 502
Text Explanation :
As the digits appear in ascending order, there is only one way in which selected group of integers can be arranged.
Thus for two digit number, we need to select two digits.
This can be done in 9C2 = 36 ways
As nCm =9C(n−m) ; 9C2 = 9C7 = Number of ways in which number can have 2 or 7 digits = 9C2 = 9C7 = 36 ways
Number of ways in which number can have 3 or 6 digits = 9C3 = 84 ways
Number of ways in which number can have 4 or 5 digits = 9C4 = 126 ways
Number of ways in which number can have 8 digits = 9C8 = 8 ways
Number of ways in which number can have 9 digits = 1 ways
1 + 8 + 2(36) + 2(84) + 2(126) = 502 numbers have 2 or more distinct digits such that the digits appear in ascending order.
Hence, 502.
Workspace:
In a tournament, there are 43 junior level and 51 senior level participants. Each pair of juniors play one match. Each pair of seniors play one match. There is no junior versus senior match. The number of girl versus girl matches in junior level is 153, while the number of boy versus boy matches in senior level is 276. The number of matches a boy plays against a girl is
Answer: 1098
Text Explanation :
The number of matches played in a group of ‘n’ peope =
The number of girl vs girl matches in junior level = 153.
Therefore, = 153 ⇒ n = 18
Therefore there are 18 girls at junior level.
⇒ There are 43 - 18 = 25 boys at junior level.
The number of boy vs boy matches in senior level = 276.
Therefore, = 276 ⇒ n = 24
Therefore there are 24 boys at senior level.
⇒ There are 51 - 24 = 27 girls at senior level.
Therefore, we have
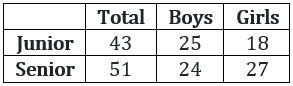
Therefore, the number of boys vs girls matches = 25 × 18 + 24 × 27 = 1098
Hence, 1098.
Workspace:
The number of solutions (x, y, z) to the equation x – y – z = 25, where x, y, and z are positive integers such that x ≤ 40, y ≤ 12, and z ≤ 12 is
- (a)
101
- (b)
99
- (c)
87
- (d)
105
Answer: Option B
Text Explanation :
x = 25 + y + z. The possible values of x, y, z and the corresponding number of values of y, z are tabulated below (x, y, z are positive integers).
We see that 27 ≤ x ≤ 40.
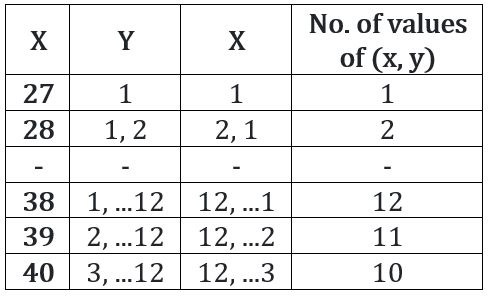
The number of solutions is 1 + 2 + … + 12 + 11 + 10 = 78 + 21 = 99.
Hence, option (b).
Workspace:
Let AB, CD, EF, GH, and JK be five diameters of a circle with center at O. In how many ways can three points be chosen out of A, B, C, D, E, F, G, H, J, K, and O so as to form a triangle?
Answer: 160
Text Explanation :
There are 5 pairs of diametrically opposite points and the centre O.
If O is not selected, the number of triangles = 10C3 = 120.
If O is selected, the other two points can be selected in 10C2 - 5 = 40 ways. (when 3 points on a diameter are selected we will not get a triangle)
The number of triangles is = 120 + 40 = 160.
Alternately,
No. of ways of choosing 3 points out of given 11 points = 11C3 = 165.
Out of these 165 ways, 5 of these would give us 3 points on the diameters mentioned, which will not form a triangle.
Hence, no. of triangles = 165 - 5 = 160.
Hence, 160.
Workspace:
In how many ways can 7 identical erasers be distributed among 4 kids in such a way that each kid gets at least one eraser but nobody gets more than 3 erasers?
- (a)
16
- (b)
20
- (c)
14
- (d)
15
Answer: Option A
Text Explanation :
After giving one eraser to each of the 4 kids, there are 3 left.
They can split 2, 1 or 1, 1, 1. (No kid can get 4)
Number of ways of 2, 1 split = 4P2
Number of ways of 1, 1, 1 split = 4C3
There are 4P2 + 4C3, i.e., 16 ways of distributing the erasers.
Alternately,
Let the number of erasers given to the 4 kids be w, x, y, z.
w + x + y + z = 7.
After giving at least 1 eraser to each, 3 erasers will be left.
w' + x' + y' + z' = 3
The number of positive integral solutions is 3 + 4 - 1C4 - 1, i.e. 20. This includes (4,1,1,1); (1,4,1,1); (1,1,4,1); (1,1,1,4).
The required number = 20 – 4 = 16.
Hence, option (a).
Workspace:
In how many ways can 8 identical pens be distributed among Amal, Bimal, and Kamal so that Amal gets at least 1 pen, Bimal gets at least 2 pens, and Kamal gets at least 3 pens?
Answer: 6
Text Explanation :
Out of 8 pens, Amal, Bimal and Kamal get at least 1, 2 and 3 pens.
So out of 8, pens 8 – (1 + 2 + 3) = 2 identical pens are to be distributed amongst 3 people.
So the number of ways in which 2 identical pens can be distributed amongst 3 people
= 2+3-1C3-1 = 4C2 or 6 ways.
Hence, 6.
Workspace:
How many four digit numbers, which are divisible by 6, can be formed using the digits 0, 2, 3, 4, 6, such that no digit is used more than once and 0 does not occur in the left-most position?
Answer: 50
Text Explanation :
For the 4 digit number to be divisible by 6, the sum of the digits of the 4 digit number has to be a multiple of 3 and the unit (right most) digit has to be an even number.
The combination of 4 digits that add upto a multiple of 3 are (0, 2, 3, 4), (0, 2, 4, 6) and (2, 3, 4, 6)
Case 1: Combination (0, 2, 3, 4)
For this combination the required number can start with 2, 3 or 4.
First digit 2: The last digit can be 0 or 4. The 2nd and 3rd digit from the left can be one 0/4 or 3. So a total of 4 possibilities.
First digit 4: Here too the number of possibilities is 4 as the 2nd and 3rd digit from the left can be one of 0/2 or 3.
First digit 3: Digits 0, 2 and 4 can be in any order as the 2nd, 3rd and 4th digit from the left. So a total of 3! or 6 possibilities.
So number of possibilities with combination (0, 2, 3, 4) = 4 + 4 + 6 = 14
Case 2: Combination (0, 2, 4, 6)
The first digit can be anyone of 2, 4 or 6 i.e., 3 possibilities. The 2nd digit can be anyone from 0/2/4/6 but apart from the one used in the left most digit i.e., 3 possibilities. The 3rd digit from the left will be any one from 0/2/4/6 but apart from the 2 digits used in the leftmost or 2nd leftmost digit i.e., 2 possibilities. The extreme right digit will be the last digit after 3 out of these 4 digits are used in the first 3 digits from the left.
So total number of possibilities = 3 × 3 × 2 = 18
Case 3: Combination (2, 3, 4, 6)
The units digit has to be one amongst 2, 4 or 6 i.e., 3 possibilities. So first 3 digits from left will be 3 and two amongst 2/4/6 (i.e., except that digit which is not chosen as the right most digit) and can be arranged in 3! or 6 ways
So number of possibilities with combination (2, 3, 4, 6) is 6 × 3 = 18
So number of 4 digits numbers that can be formed using digits 0, 2, 3, 4 and 6 is 14 + 18 + 18 = 50
Hence, 50.
Workspace:
Directions for next 2 questions:
The figure below shows the plan of a town. The streets are at right angles to each other. A rectangular park (P) is situated inside the town with a diagonal road running through it. There is also a prohibited region (D) in the town.
.png)
Neelam rides her bicycle from her house at A to her office at B, taking the shortest path. Then the number of possible shortest paths that she can choose is
- (a)
60
- (b)
75
- (c)
45
- (d)
90
- (e)
72
Answer: Option D
Text Explanation :
.png)
We can find the number of shortest possible paths from A to E either by trial and error or by using combinations.
Note that to travel from A to E, we have to take 2 roads to the right and 2 roads downwards (in the diagram) in order that we follow the shortest path. In other words, we have to use 2 + 2 = 4 roads, out of which 2 are towards right and 2 are downwards.
This is equivalent to selecting 2 things (roads towards right) out of 4 things (roads). (The remaining two roads will be downwards.)
The number of ways of doing this is 4C2 = 4!/(2!×2!) = 6
∴ From point A to E, there are 6 ways to reach with the minimum distance travelled.
Here E to F is the shortest distance because the third side of a triangle is always less than the sum of the other two sides.
From point F to B, there are 6C4 = 6!/(4!×2!) = 15 ways to reach with the minimum distance travelled.
∴ There are 15 × 6 = 90 shortest paths that Neelam can choose.
Hence, option (d).
Workspace:
Neelam rides her bicycle from her house at A to her club at C, via B taking the shortest path. Then the number of possible shortest paths that she can choose is
- (a)
1170
- (b)
630
- (c)
792
- (d)
1200
- (e)
936
Answer: Option A
Text Explanation :
.png)
From point A to B, there are 90 paths possible with the minimum distance travelled.
We can travel from B to C in two ways
1. B – K – M – C
To travel from B to K, we have to take 6 roads, out of which one is towards left and 5 are upwards.
There are 6!/(5!×1!) = 6 ways to do this. (Refer to the explanation in the first question of this set.)
2. B – N – C
To travel from B to N, we have to take 7 roads, out of which one is towards left and 6 are upwards.
There are 7!/(6!×1!) = 7 ways to do this.
∴ There are 6 + 7 = 13 ways in which we can travel from B to C.
∴ Overall there are 90 × 13 = 1170 paths possible
Hence, option (a).
Workspace:
How many integers, greater than 999 but not greater than 4000, can be formed with the digits 0, 1, 2, 3 and 4, if repetition of digits is allowed?
- (a)
499
- (b)
500
- (c)
375
- (d)
376
- (e)
501
Answer: Option D
Text Explanation :
The minimum number that can be formed is 1000, hence the number is a 4-digit number,
The maximum number that can be formed is 4000.
As 4000 is the only number in which the first digit is 4, first let us calculate the numbers less than 4000 and then we will add 1 to it.
∴ First digit can be 1, 2 or 3.
Remaining 3 digits can be any of the 5 digits.
∴ Total numbers that can be formed, which are less than 4000 = 3 × 5 × 5 × 5 = 375
∴ Total numbers that satisfy the given condition = 375 + 1 = 376
Hence, option (d).
Workspace:
What is the number of distinct terms in the expansion of (a + b + c)20?
- (a)
231
- (b)
253
- (c)
242
- (d)
210
- (e)
228
Answer: Option A
Text Explanation :
Consider (a + b + c)20
Each term in the expansion of (a + b + c)20 can be written as 20Cr × ax × by × cz, where (x + y + z) = 20
Number of distinct terms in the expansion will be same as the number of distinct pairs of x, y and z.
∴ We have to divide 20 into three parts which can be done by using the distribution rule = n+r-1Cr-1
Where,
n is number of things to be distributed.
r is number of parts into which the things are to be distributed.
∴ To divide 20 into 3 parts we have,
20+3-1C3-1 = 22C2 = = 11 × 21 = 231
Alternatively,
This can be solved without using much knowledge of permutations and combinations as follows,
(a + b + c)1 = a + b + c [i.e. 3 terms = (1 + 2) terms]
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac [i.e. 6 terms = (1 + 2 + 3) terms]
(a + b + c)3 = a3 + b3 + c3 + 6abc + 3ab2 + 3ac2 + 3a2b + 3bc2 + 3a2c + 3b2c [i.e. 10 terms = (1 + 2 + 3 + 4) terms]
Similarly,
(a + b + c)n will have (1 + 2 + 3 + … + (n + 1)) terms
∴ (a + b + c)20 will have (1 + 2 + 3 + … + 21) = 231 terms
Hence, option (a).
Workspace:
Answer the next 2 questions based on the information given below.
Let S be the set of all pairs (i, j) where 1 ≤ i < j ≤ n and n ≥ 4. Any two distinct members of S are called “friends” if they have one constituent of the pairs in common and “enemies” otherwise. For example, if n = 4, then S = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)}. Here, (1, 2) and (1, 3) are friends, (1, 2) and (2, 3) are also friends, but (1, 4) and (2, 3) are enemies.
For general n, how many enemies will each member of S have?
- (a)
n – 3
- (b)
- (c)
2n - 7
- (d)
- (e)
Answer: Option D
Text Explanation :
Enemies of every pair are the pairs formed with all numbers other than the two in the member itself.
∴ If there are n elements then each member has
Hence, option (d).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report