Concept: Mensuration

A solid in which the top and bottom surfaces are identical polygons and the lateral (vertical) surfaces are rectangular in shape and perpendicular to the top and bottom surfaces is known as a right prism. In a right prism, the corresponding sides of the top and bottom polygons are parallel.

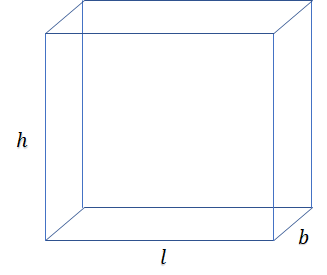
• Volume (V) = lbh

• Total Surface Area (TSA) = 2(lb + bh + lh)

• Lateral Surface Area (LSA) = 2(l + b)h

• Surface Diagonals (12) = $\sqrt{l^2+b^2}$ or $\sqrt{h^2+b^2}$ or $\sqrt{l^2+h^2}$

• Body Diagonal (4) = $\sqrt{l^2+b^2+h^2}$

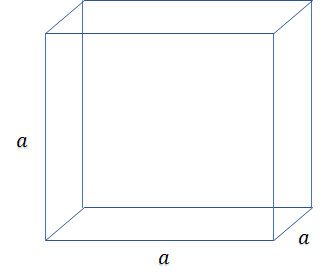
• Volume (V) = a³

• Total Surface Area (TSA) = 6a²

• Lateral Surface Area (LSA) = 4a²

• Surface Diagonal (12) = a√2

• Body Diagonal (4) = a√3

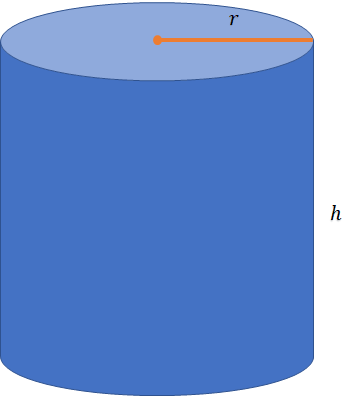
• Volume (V) = πr²h

• Lateral Surface Area (LSA) = 2πrh

• Total Surface Area (TSA) = LSA + 2πr²

A right pyramid is a solid in which: The bottom surface (i.e. base) is a polygon, each vertex of which is joined with the help of slanted edges to a single vertex at the top. The lateral (slanted−vertical) surfaces are triangular in shape. The line joining the top vertex to the centre of the polygon which forms the bottom surface (also known as the height) is perpendicular to the bottom surface.

• Volume (V) = ⅓ × base area × height

• Lateral Surface Area (LSA) = ½ × base perimeter × slant height

• Total Surface Area (TSA) = LSA + base area

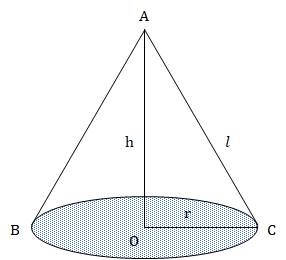
• Volume (V) = ⅓ × πr²h

• Lateral Surface Area (LSA) = πrl

• Total Surface Area (TSA) = LSA + πr²

• Slant height (l) = $\sqrt{r^2+h^2}$

When a cone is made out of a sector of a circle of radius R

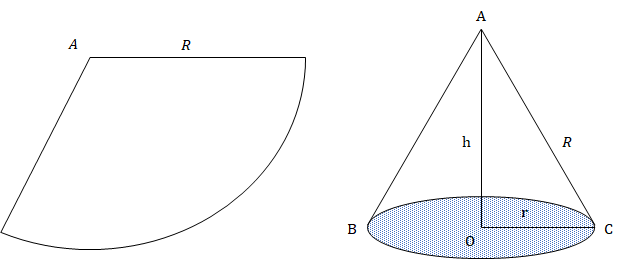
• Slant height of the cone (l) = R

• Radius of the cone (r) = $\frac{\mathrm{𝜃}}{\mathrm{360°}}$ × R

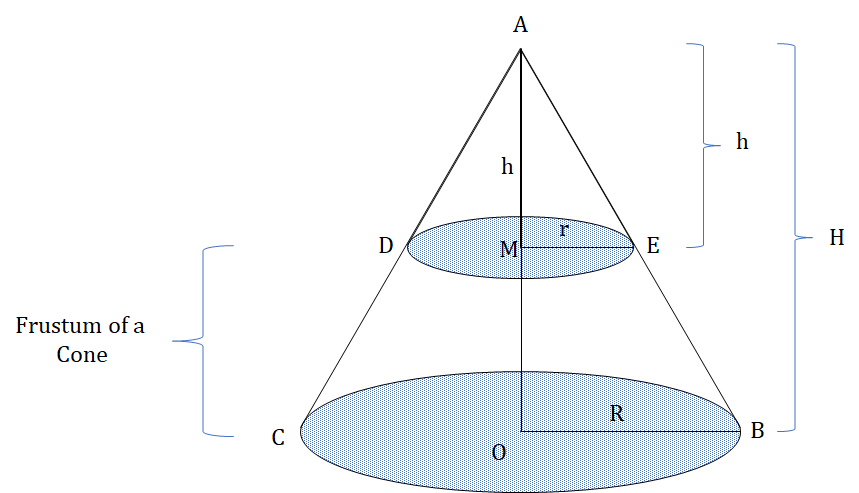
• Volume (V) = ⅓ × πH_f(R² + Rr + r²)

• Lateral Surface Area = π(R + r)l_f

• Total Surface Area = LSA + π(R² + r²)

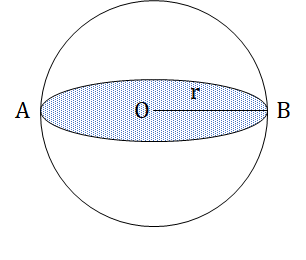
• Volume (V) = $\frac{4}{3}$ × πr³

• Total Surface Area (TSA) = 4πr²

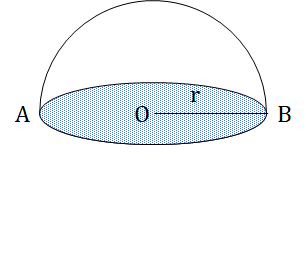
• Volume (V) = $\frac{2}{3}$ × πr³

• Curved Surface Area (CSA) = 2πr²

• Total Surface Area (TSA) = 3πr²