Concept: Time, Speed and Distance

Example: A plane covers the distance of Mumbai to Bhopal in 1 hr and 30 minutes. Calculate the speed of the plane if the distance between Bhopal and Mumbai is 800 kms.

Solution:
Speed = $\frac{\mathrm{Distance}}{\mathrm{Time}}$

⇒ Speed = $\frac{800}{1.5}$ = 533$\frac{1}{3}$ km/h

Example: Express 27 km/h into m/s.

Solution:
27 km/h = 27 × $\frac{5}{18}$ m/s = 7.5 m/s

Example: Express 12 m/s into km/h.

Solution:
12 m/s = 12 × $\frac{18}{5}$ kmph = 43.2 km/h

Example: A man travels to his office 50 kms in two hours. He does it partly in a chartered bus which travels at the rate of 40 km/h and partly on foot at the rate of 10 km/h. Find how much distance does the man travel on foot?

Solution:
Let x be the distance travelled by bus so the distance travelled on foot = 50 – x

⇒ $\frac{\mathrm{x}}{40}$ + $\frac{\mathrm{(50\; -\; x)}}{10}$ = 2 

⇒ x = 40 kms

Example: Rashmi walks to her bus stop at 5 km/h and reaches there late by 10 minutes. On the next day she increases her speed to 6 km/h and reaches the bus stop 10 minutes early. How far is the bus stop?

Solution:
Let x be the distance of the bus stop

The difference in time taken for both speeds = 10 + 10 = 20 minutes = 20/60 hours

⇒ $\frac{\mathrm{x}}{5}$ – $\frac{\mathrm{x}}{6}$ = $\frac{20}{60}$

⇒ x = 10 km/h

Alternate Method:
Ratio of speeds = 5 : 6, hence the ratio of time taken = 6 : 5

So, we can assume that the actual times taken are 6x and 5x respectively.

Hence, time taken at 6 kmph in minutes = 5 × 20 = 100 minutes or 5/3 hours

The distance = 6 × 5/3 = 10 kms

Example: Amar travels at a speed of 10 kmph for 2 hours and then increases his speed to 20 kmph for next 1 hour. What is his average speed for the entire distance.

Solution:
Total distance travelled by Amar = 10 × 2 + 20 × 1 = 40 kms.
Total time taken to cover this distance = 2 + 1 = 3 hours.
∴ Average speed = 40/3 kmph.

Example: A boy covers some distance at the rate of 15 km/h on a bike, and he returns back at a speed of 12 km/h. If the time taken for the travel is not known, find the average speed at which the boy travels?

Solution:
Let the distance covered by the boy each way b “x”

Average speed = D/T

T = Total Time = $\frac{x}{15}$ + $\frac{x}{12}$    (Time = $\frac{\mathrm{Distance}}{\mathrm{Speed}}$)

Example: Deepak covers a total distance of 300 kms at three different speeds of 30, 60 and 80 kmph. Find his average speed for the entire duration.

Solution:
Deepak covers 100 kms at each of the three different speeds.
Total time taken = $\frac{100}{30}$ + $\frac{100}{60}$ + $\frac{100}{80}$
∴ Average speed = $\frac{300}{{\displaystyle \frac{100}{30}}+{\displaystyle \frac{100}{60}}+{\displaystyle \frac{100}{80}}}$ = $\frac{3\times 30\times 60\times 80}{30\times 60+60\times 80+80\times 30}$ = 48 kmph.

Example: If Karan travels 30 kms at 30 kmph, at what speed should he travel the next 30 kms such that his average speed for the entire journey is 48 kmph.

Solution:
Total distance travelled by Karan = 30 + 30 = 60 kms

Let speed for second part of the journey be ‘s’ kmph.

∴ Total time taken = $\frac{30}{30}$ + $\frac{30}{\mathrm{s}}$

⇒ Average speed = 48 = $\frac{60}{{\displaystyle \frac{30}{30}}+{\displaystyle \frac{30}{s}}}$

⇒ 4 =  5/(1+30/s)

⇒ 4 + $\frac{120}{\mathrm{s}}$ = 5

⇒ s = 120 kmph

Example: Suresh travels by a hovercraft from Vashi to Gateway of India. Every day he catches the Hovercraft at 9 a.m. One day, however, he is delayed by five minutes because of a railway crossing which he has to cross to reach Vashi from his home. He normally takes 20 minutes to reach Vashi by his car from Panvel just 30 kms from Vashi. If the railway crossing is 21 kms from Panvel, find at what speed should. Suresh travel in order to reach on time?

Solution:
The average speed of Suresh S = 20/30 = 2/3 km/h
Suresh must have travelled from Panvel to the railway crossing at the normal speed. The time required by Suresh to travel the remaining distance from Railway crossing to Vashi is = 2/3 × 9 = 6 minutes, out of these 6 minutes required by Suresh, 5 minutes go waste due to the delay at the crossing. This results in Suresh’s being required to travel the remaining distance of 9 kms in one hour. Hence, required speed = 9/1 = 9 km/h

Example: If two persons start at the same time from two points A, B, towards each other and after crossing each other they take X and Y hours in reaching B and A respectively then what is the ratio of the speed of one with respect to the other?

Solution:
let the man starting from A be P and the man starting from B be Q then let their speeds be 'p' and 'q' respectively.

Let C be point where they meet after t hours.

Distance AC is covered by P in t hours and by Q in Y hours.

⇒ AC = p × t = q × Y

⇒ $\frac{p}{q}$ = $\frac{Y}{t}$ ...(1)

Similary, Distance BC is covered by P in X hours and by Q in t hours.

⇒ BC = p × X = q × t

⇒ $\frac{p}{q}$ = $\frac{t}{X}$ ...(2)

Multiplying (1) and (2), we get

⇒ ${\left(\frac{p}{q}\right)}^2$ = $\frac{Y}{X}$

∴ $\frac{p}{q}$ = $\sqrt{\frac{Y}{X}}$

Example: A policeman running at 12 kmph is trying to catch a thief running at 8 kmph. If the thief is currently 16 kms ahead of the policeman, how long will it take to catch the thief

Solution:
Since both of them are running in same direction, relative speed of policeman w.r.t. thief = 12 - 8 = 4 kmph

∴ time required to catch the thief = 16/4 = 4 hours.

Example: A train travelling at a rate of 25 km/h leaves Bhopal at 9 am and another train travelling in the same direction at a speed of 35 km/h starts at 1 pm. How many kms from Bhopal would both the trains meet and when would they meet?

Solution:
The first train travels from 9 am till 1 pm i.e. for 4 hours at 25 kmph.

Distance travelled by it = 4 × 25 = 100 kms.

Now, the second train starts from Bhopal at 35 kmph.

Relative speed = 35 - 25 = 10 kmph

∴ Time taken for the two trains to meet = D/(a - b) = 100/(35 - 25) = 10 hrs

Distance of meeting point from Bhopal will be same as the distance covered by the train starting from Bhopal.

∴ The trains will meet at a distance of 10 × 35 = 350 kms from Bhopal

Example: A bus starts from Bhopal at 10 am and goes to Indore. Another bus follows at a speed of 65 km/h at 11 a.m. Find at what distance from Bhopal will the second bus catch the first bus? ( Given the speed at which the first bus moves is 50 km/h)

Solution:
 To use relative velocity let us first find out the distance between both the buses when the second bus starts moving.

In the first one hour the distance travelled by the first bus is 50 kms.

When the second bus starts moving then, since they are both moving in the same direction, the relative speed is given by : b – a

and time required by the second bus is given by : T = D/(b - a)

⇒ T = 50/(65 - 50) = 10/3 hrs

∴ distance travelled by the second  bus is = 10/3 × 65 = 216.45 kms

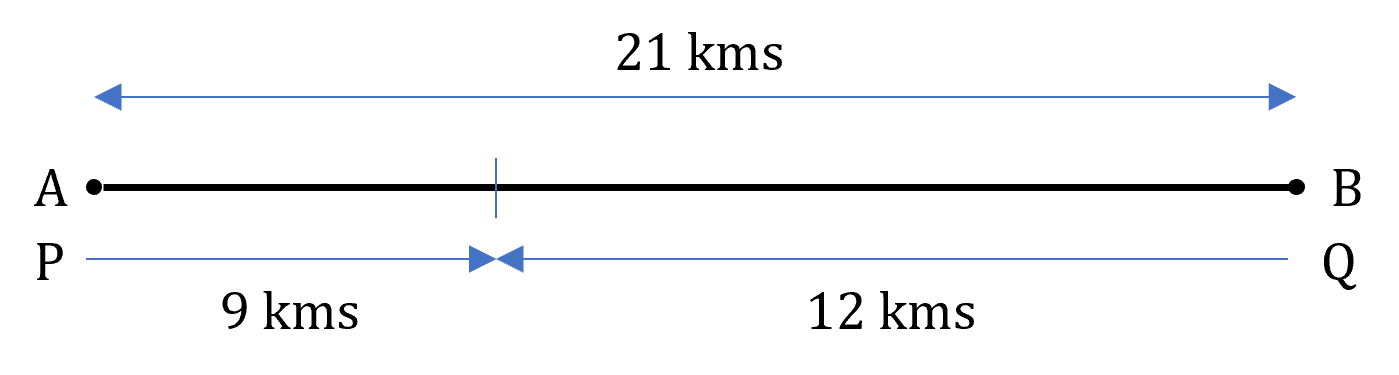
Example: Two men P and Q start from two different points A and B and move in opposite directions at speeds of 3 km/h and 4 km/h respectively. They travel to B and A respectively and again return to their respective positions. Find when and at what point from A would they both meet for the first and the second time? (Given AB = 21 kms)

Solution:
First meeting point:
Initial distance between P and Q is 21 kms and their relative speed = (3 + 4) = 7 kmph

∴ Time taken to meet for the first time = $\frac{21}{7}$ = 3 hours.

∴ Distance travelled by P in 3 hours = 3 × 3 = 9 kms

∴ The first meeting point is at a distance of 9 kms from A.

​​​​​​​

Second meetig point:
Let the second meeting point be at a distance of x kms from A.

​​​​​​​

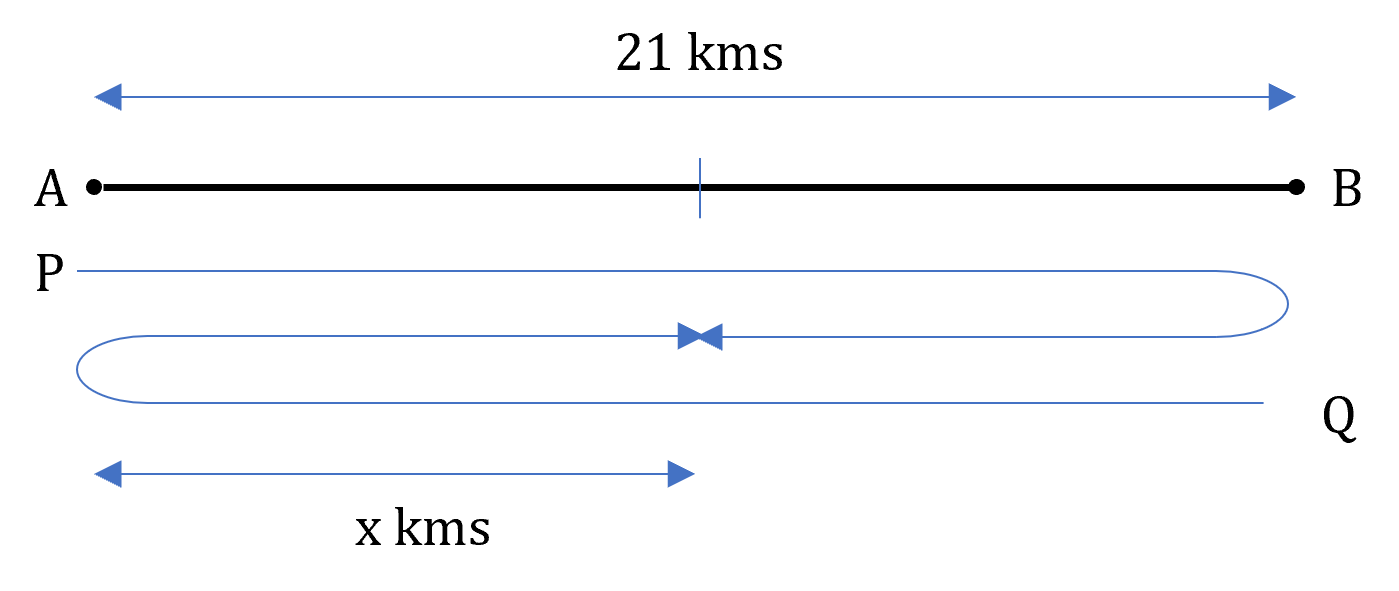
P covers a distance of (21 + 21 - x) kms to reach the second meeting point whereas Q covers a distance of (21 + x) kms to reach the second meeting point.

Both of them cover this distance in the same amount of time.

Ratio of speeds = Ratio of distances travelled.

⇒ $\frac{3}{4}$ = $\frac{\mathrm{(42\; -\; x)}}{\mathrm{(21\; +\; x)}}$

⇒ 63 + 3x = 168 - 4x

⇒ 7x = 105

⇒ x = 15

∴ The second meeting point is at a distance of 15 kms from A.

Example: Two men P and Q start from two different points A and B and move in opposite directions at speeds of 3 km/h and 7 km/h respectively. They travel to B and A respectively and again return to their respective positions. Find the time taken by them to meet for the first and the second time? (Given AB = 40 kms)

Solution:
First meeting point:
Initial distance between P and Q is 40 kms and their relative speed = (3 + 7) = 10 kmph

∴ Time taken to meet for the first time = $\frac{40}{10}$ = 4 hours.

​​​​​​​

Second meetig point:
Let the second meeting point be at a distance of x kms from A.

​​​​​​​

Since Q is much faster than P, Q will meet P for second time even before P reaches the opposite end point.

P covers a distance of x kms to reach the second meeting point whereas Q covers a distance of (40 + x) kms to reach the second meeting point.

Both of them cover this distance in the same amount of time.

Ratio of speeds = Ratio of distances travelled.

⇒ $\frac{3}{7}$ = $\frac{\mathrm{x}}{\mathrm{(40\; +\; x)}}$

⇒ 120 + 3x = 7x

⇒ 4x = 120

⇒ x = 30

∴ Time taken by P to reach second meeting point is = $\frac{30}{3}$ = 10 hours.

Example: Two trains 80 m and 120 m in length respectively are running at 45 km/h and 55 km/h. Find the time they will take to cross each other if it is known that they are travelling in opposite direction?

Solution:
The total length to be covered by both the trains together = 120 + 80 = 200 m

Since, the trains are travelling in opposite directions the relative speed will be the addition of the two given speeds = 45 + 55 = 100 km/h = 100 × 5/18 m/s

∴ Time required will be = $\frac{200}{100\times {\displaystyle \frac{5}{18}}}$ = $\frac{36}{5}$ = 7.2 sec.

Example: Two trains 80 m and 120 m in length respectively are running at 45 km/h and 55 km/h. Find the time taken by faster train to overtake the slower train?

Solution:
The total length covered by both the trains together = 120 + 80 = 200 m

Since, the trains are travelling in same directions the relative speed will be the difference of the two given speeds = 55 - 45  = 10 km/h = 10 × 5/18 m/s

∴ Time required will be = $\frac{200}{10\times {\displaystyle \frac{5}{18}}}$ = $\frac{360}{5}$ = 72 sec.

Example: A train 100 m long takes 5 seconds to cross a man walking at the rate of 5 m/s. Find the speed of the train if the man and the train are travelling in the opposite direction?

Solution:
Let the speed of the train be ‘V’ m/s

Relative speed of train and man = V + 5

The time required by the train to cross the man = 5 sec = $\frac{100}{V+5}$

Hence, V = 15 m/s.

Example: Two trains of length 100 m and 200 m are travelling in opposite directions at respective speeds of 30 and 24 kmph. How long will it take for the slower train to cross the driver of the faster train?

Solution:
Relative speed of the two trains = 24 + 30 = 54 kmph = 54 × 5/18 m/s = 15 m/s

Here the slower train has to cross the driver of faster train hence we will not be considering the length of the faster train.

∴ Required time = 200/15 = 40/3 seconds.

Example: A train crosses a bridge in 25 seconds when running at 72 km/h and crosses another bridge twice as long in 20 seconds when running at the rate of 162 km/h. Find the length of the train and the length of the bridge?

Solution:
72 km/h = 20 m/s and 162 km/h = 45 m/s

Let the length of the train and the smaller bridge be T & B respectively.

$\frac{T+B}{20}$ = 25 and $\frac{T+\mathrm{2B}}{45}$ = 20

Thus, on solving the above equations, we get T and B as 100 m and 400 m respectively.

Example: A train 120 m long and travelling at 90 km/h overtakes another train running at 72 km/h and passes the second train completely in 50 seconds. Find the length of the second train?

Solution:
Let the length of the second train be L then.

Relative speed of the two trains = 90 - 72 = 18 kmph = 5 m/s

⇒ (120 + L)/5 = 50

∴ L = 130 m

Example: Two trains, one half as long as the other, cross each other in 20 seconds and the faster one can overtake the slower one in 50 seconds. Find the speed of each of the trains if the longer train is 100 m long?

Solution:
The length of longer train = 100 m hence, that of shorter train = 50 m.

Let 'a' and 'b' be the speeds of the two trains.

∴ 150/(a + b) = 20 and 150/(a - b)=50.

⇒ a + b = 75 and a – b = 3

On solving the above equations, we get a and b as 39 and 36 m/s respectively.

Example: A man can row upstream at the rate of 16 km/h and downstream at the rate of 20 km/h. Find the speed of the man in still water and also the speed of the flow of water.

Solution:
S_U = b - r = 16 and S_D = x + y = 20.

On solving the equations we get x = 18 km/h and y = 2 km/h

Example: A man can row 6 kms in still water and it takes him thrice as long as to go up the stream as it takes to go down the stream. Find the rate of the stream.

Solution:
Let the distance to be covered up and down the stream be D then he the time required by him to go down the stream and up the stream respectively, are
T_D = $\frac{D}{6+y}$ and T_U = $\frac{D}{6-y}$

Given, T_U = 3 × _D

⇒ $\frac{D}{6-y}$ = 3 × $\frac{D}{6+y}$

On solving the given equation we get y = 3

Example: A man rows 30 kms upstream and 44 kms downstream in 10 hours on some day and the next day he rows 40 kms upstream and 55 kms downstream in 13 hours. Find the speed of the man in still water?

Solution:
Let the speed of man be ‘b’ km/h and that of the flow of water be ‘r’ then the sum of the upstream and the downstream times must be equal to the total time required by the man to travel both the distances.

$\frac{30}{\mathrm{u}}$ + $\frac{44}{\mathrm{d}}$ = 10 and $\frac{40}{\mathrm{u}}$ + $\frac{55}{\mathrm{d}}$ = 13

Now, d = b + r and u = b - r

On solving the above two equations we get b = 8 kmph and r = 3 kmph

Example: Amar can swim up to a certain distance with the current in 6 hours and return the same distance in 9 hours. If the river flows at the rate of 3 km/h then find the speed of Ramesh in still water?

Solution:
Let “D” be the distance that Amar swims with the current so he would have covered the same distance against the current also. Also let the speed with which Amar can swim be “x” then we have the following equations.

⇒ $\frac{\mathrm{D}}{\mathrm{(x\; +\; 3)}}$ = 6 and $\frac{\mathrm{D}}{\mathrm{(x\; -\; 3)}}$ = 9

Thus, x = 15 km/h

Example: In a 900 meter race, A beats B by 90 meters or 10 seconds. Find:
(a) Speed of B.
(b) Speed of A.
(c) Time taken by A to complete the race.

Solution:
(a) A beats B by 90 meters. It implies that when A finishes the race B is still 90 meters behind him.

Now, A beats B by 10 seconds implies that B reaches the finish line 10 seconds after A does.

Hence, B covers 90 meters in 10 seconds.

∴ S_B = 90/10 = 9 meters/sec.

(b) Now, by the time A covers 900 meters (i.e. reaches finish line), B covers (900 - 90 = ) 810 meters.

∴ $\frac{S_A}{S_B}$ = $\frac{900}{810}$ = $\frac{10}{9}$

⇒ Speed of A = 10 m/s

(c) Time taken by A to complete the race = 900/10 = 90 seconds.

Example: In a km race A gives B a head start of 100 meters and still beats him by 100 meters or 5 seconds. Find the speed of A.

Solution:
A beats B by 100 meters or 5 seconds implies that B covers the final 100 meters in 5 seconds.

∴ S_B = 100/5 = 20 meters/sec.

A starts running when B is 100 meters ahead. Hence, by the time A covers 1000 meters (i.e. reaches finish line), B covers (1000 - 100 - 100 = ) 800 meters.

∴ $\frac{S_A}{S_B}$ = $\frac{1000}{800}$ = $\frac{5}{4}$

⇒ Speed of A = 25 m/s

Example: In a km race A beats B by 200 meters and B beats C by 100 meters. Find by how much does A beat C by?

Solution:
Method 1:
A beats B by 200 meters
∴ $\frac{S_A}{S_B}$ = $\frac{1000}{\mathrm{(1000\; -\; 200)}}$ = $\frac{5}{4}$ ...(1)

B beats C by 100 meters
∴ $\frac{S_B}{S_C}$ = $\frac{1000}{\mathrm{(1000\; -\; 100)}}$ = $\frac{10}{9}$ ...(2)

Multiplying (1) and (2) we get

⇒ $\frac{S_A}{S_C}$ = $\frac{50}{36}$

Since time taken is same, ratio of speed = ratio of distance covered

∴ $\frac{50}{36}$ = $\frac{1000}{\mathrm{d}}$

⇒ Distance covered by C (d) = 720 meters

Hence, A beats C by 1000 - 720 = 280 meters.

Method 2:
A beats B by 200 meters. It means by the time A covers 1000 meters, B covers 800 meters.

B beats C by 100 meters. It means by the time B covers 1000 meters C is 100 meters behind

∴ when B covers 800 meters, C will be 800 × $\frac{100}{1000}$ = 80 meters behind B

⇒ When A finishes, B is 200 behind A and C is another 80 meters behind B.

∴ A beats C by 200 + 80 = 280 meters.

Example: Two people A and B are running around a 3000 meters circular track at speeds of 5 m/s and 3 m/s in opposite directions. Find the time taken for them to meet
(a) anywhere on the circle (b) at the starting point

Solution:
(a) Time to meet anywhere on the circle = $\frac{3000}{\mathrm{(5\; +\; 3)}}$ = 375 secs

(b) Time to meet at the starting point = LCM$\left[\frac{\mathrm{3000}}{5},\frac{\mathrm{3000}}{3}\right]$ = 3000 secs

Example: Two people A and B are running around a 3000 meters circular track at speeds of 5 m/s and 3 m/s in same directions. Find the time taken for them to meet
(a) anywhere on the circle (b) at the starting point

Solution:
(a) Time to meet anywhere on the circle = $\frac{3000}{\mathrm{(5\; -\; 3)}}$ = 1500 secs

(b) Time to meet at the starting point = LCM$\left[\frac{\mathrm{3000}}{5},\frac{\mathrm{3000}}{3}\right]$ = 3000 secs

Example: Two people A and B are running around a circular track at speeds of 30 m/s and 20 m/s. Find the number of distinct meeting poinst if
(a) they are running in opposite direction (b) they are running in same direction

Solution:
Simplified ratio of speeds = 30 : 20 = 3 : 2

of distinct meeting points when

(a) they are running in opposite direction = 3 + 2 = 5

(b) they are running in same direction = 3 - 2 = 1

Example: A man can go up a moving down escalator in 60 seconds. If escalator is moving at 2 steps/sec and speed of the person is 3 steps/sec on stationery escalator, find the time required by the man to go up when the escalator is not moving.

Solution:
Let the number of steps be 'N'.

∴ Effective speed of man while going up = (3 - 2) = 1 step/sec

∴ $\frac{\mathrm{N}}{1}$ = 60

⇒ N = 60 steps

Now, time taken by the man to go up when the escalator is not moving = 60/3 = 20 seconds

Example: When Akash walks down, he takes 1 minute on an escalator that is moving down but takes 40 seconds when he runs down. He takes 20 steps when he is walking whereas he takes 30 steps when he is running. Calculate the total number of steps in the escalator?

Solution:
Let the number of steps be 'N', speeds of Akash while walking and running be 'w' and 'r' respectively and speed of escalator be 'e' steps/sec.

Case 1: When Akash walks down
effective speed of Akash = w + e

⇒ N = (w + e) × 60

⇒ N = w × 60 + e × 60

⇒ N = 20 + e × 60 [Akash himself takes 20 steps while walkind, w × 60 = 20]

⇒ N = 20 + 60e ...(1)

Case 2: When Akash runs down
effective speed of Akash = r + e

⇒ N = (r + e) × 40

⇒ N = r × 40 + e × 40

⇒ N = 30 + e × 40 [Akash himself takes 20 steps while walking, r × 40 = 30]

⇒ N = 30 + 40e ...(2)

Solving (1) and (2) we get
e = 0.5 steps/sec and N = 50 steps.