Data Sufficiency - Previous Year CAT/MBA Questions
The best way to prepare for Data Sufficiency is by going through the previous year Data Sufficiency CAT questions. Here we bring you all previous year Data Sufficiency CAT questions along with detailed solutions.
Click here for previous year questions of other topics.
It would be best if you clear your concepts before you practice previous year Data Sufficiency CAT questions.
Each question is followed by two statements, A and B. Answer each question using the following instructions:
Mark option (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark option (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark option (3) if the question can be answered by using either statement alone.
Mark option (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark option (5) if the question cannot be answered on the basis of the two statements.
In a single elimination tournament, any player is eliminated with a single loss. The tournament is played in multiple rounds subject to the following rules:
a. If the number of players, say n, in any round is even, then the players are grouped in to n/2 pairs. The players in each pair play a match against each other and the winner moves on to the next round.
b. If the number of players, say n, in any round is odd, then one of them is given a bye, that is, he automatically moves on to the next round. The remaining (n − 1) players are grouped into (n − 1)/2 pairs. The players in each pair play a match against each other and the winner moves on to the next round. No player gets more than one bye in the entire tournament.
Thus, if n is even, then n/2 players move on to the next round while if n is odd, then (n + 1)/2 players move on to the next round. The process is continued till the final round, which obviously is played between two players. The winner in the final round is the champion of the tournament.
What is the number of matches played by the champion?
A: The entry list for the tournament consists of 83 players.
B: The champion received one bye.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
- (e)
5
Answer: Option D
Text Explanation :
From statement (A) alone:
The entry list for the tournament consists of 83 players.
In round 1, 1 of the 83 players gets a bye and directly moves on to the next round.
∴ 42 players move on to round 2.
Similarly, 21 players move on to round 3, 11 players move on to round 4, 6 players move on to round 5, 3 players move on to round 6, 2 players move on to round 7.
The winner of the tournament would have played one match in each of the rounds; i.e. a total of 7 matches, provided he doesn’t get a bye.
However, we are not told whether or not the champion received a bye at some point in the tournament.
∴ We cannot answer the question on the basis of statement (A) alone.
From statement (B) alone:
The champion received one bye.
From this statement, we cannot find the number of matches played by the champion.
∴ We cannot answer the question on the basis of statement (B) alone.
From both the statements (A) and (B) together:
The champion must have played 7 matches if he did not receive any bye.
But it is given that the champion has got one bye in the tournament.
∴ He must have played only 6 matches.
∴ We can answer the question using both the statements (A) and (B) together.
Hence, option (d).
Workspace:
If the number of players, say n, in the first round was between 65 and 128, then what is the exact value of n?
A. Exactly one player received a bye in the entire tournament.
B. One player received a bye while moving on to the fourth round from the third round
- (a)
1
- (b)
2
- (c)
3
- (d)
4
- (e)
5
Answer: Option D
Text Explanation :
From statement (A) alone:
Exactly 1 player received a bye in the entire tournament. We get many values of n between 65 and 128 that satisfy this condition.
For example, n can have the value 124 in round 1, to follow the pattern, [124-62-31-16-8-4-2-1].
Also, n can have the value 127 in round 1, to follow the pattern, [127-64-32-16-8-4-2-1].
∴ We cannot answer the question on the basis of statement (A) alone.
From statement (B) alone:
One player received a bye while moving on to the fourth round from the third round.
Here also, we get multiple values of n.
For example, n can have the value 124 in round 1, where 1 player received a bye while moving from round 3 to round 4 following the pattern, [124-62-31-16-8-4-2-1].
Also, n can have the value 122 in round 1, where 1 player received a bye while moving from round 3 to round 4 following the pattern, [122-61-31-16-8-4-2-1].
∴ We cannot answer the question on the basis of statement (B) alone.
From statements (A) and (B) together:
n can only have the value 124 in round 1, where exactly 1 player received a bye while moving from round 3 to round 4 following the pattern [124-62-31-16-8-4-2-1].
∴ We can answer the question using both the statements (A) and (B) together.
Hence, option (d).
Note: An analysis of how 124 was arrived at when using both conditions together:
Let the number of players in the first round be n. Since only one player gets a bye, and that too when moving from the third to the fourth round, hence we have the following conditions:
1. There will be n players in the first round, where n is even.
2. There will be n/2 players in the second round, where n/2 is even.
3. There will be n/4 players in the third round, where n/4 is odd.
4. There will be players in the fourth round, where should be even.
5. All numbers of players in the subsequent rounds should also be even.
From condition 3, we can conclude that:
where k is an integer
Hence, n = 16k – 4; so, within the given range, n could be 76 or 92 or 108 or 124.
Writing the pattern for each of the above possible values of n, we have:
76: [76-38-19-10-5-3-2-1]
92: [92-46-23-12-6-3-2-1]
108: [108-54-27-14-7-4-2-1]
124: [124-62-31-16-8-4-2-1]
We see that only 124 satisfies condition 5.
Hence, option (d).
Workspace:
Each question is followed by two statements A and B. Answer each question using the following instructions.
Mark (1) if the question can be answered by using statement A alone but not by using statement B alone.
Mark (2) if the question can be answered by using statement B alone but not by using statement A alone.
Mark (3) if the question can be answered by using both the statements together but not by using either of the statements alone.
Mark (4) if the question cannot be answered on the basis of the two statements.
The average weight of a class of 100 students is 45 kg. The class consists of two sections, I and II, each with 50 students. The average weight, WI, of Section I is smaller than the average weight, WII, of Section II. If the heaviest student, say Deepak, of Section II is moved to Section I, and the lightest student, say Poonam, of Section I is moved to Section II, then the average weights of the two sections are switched, i.e., the average weight of Section I becomes WII and that of Section II becomes WI. What is the weight of Poonam?
A. WII – WI = 1.0
B. Moving Deepak from Section II to I (without any move from I to II) makes the average weights of the two sections equal.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option C
Text Explanation :
Let the weights of Deepak and Poonam be d and p respectively.
(50WII + 50WI)/100 = 45
∴ WII + WI = 90 ...(i)
50WI + d – p = 50WII
50WII – d + p = 50WI
∴ 50(WII – WI) = d – p ...(ii)
From Statement A, WII – WI = 1 ...(iii)
From (i), (ii) and (iii)
WI and WII can be found. Also, d – p = 50 ...(iv)
However this information does not give us the value of p. Statement A is insufficient to answer the question.
From Statement B,
WI = WII = (SumI + d)/51 = (SumII – d)/49
∴ 49(SumI) + 49d = 51(SumII) – 51d
∴ 100d = 51(50WII) – 49(50WI)
∴ 2d = 51WII – 49WI ...(v)
This alone cannot help us find the value of p. Statement B is insufficient to answer the question.
Considering both statements together, we have values of WI and WII, which can be substituted in (v) to find d, which can be used to find p using (iv).
Hence, option (c).
Workspace:
Each question is followed by two statements, I and II. Answer each question using the following instructions:
Mark (1) if the question can be answered by using statement I alone but not by using statement II alone.
Mark (2) if the question can be answered by using statement II alone but not by using statement I alone.
Mark (3) if the question can be answered by using either of the statements alone.
Mark (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark (5) if the question cannot be answered by using any of the statements.
In a football match, at the half-time, Mahindra and Mahindra Club was trailing by three goals. Did it win the match?
I. In the second-half Mahindra and Mahindra Club scored four goals.
II. The opponent scored four goals in the match.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
- (e)
5
Answer: Option E
Text Explanation :
From Statement I, the MM club scored 4 goals in the second half. The number of goals scored by the opponent is not known. So the winner cannot be determined. Statement I is insufficient.
From Statement II, the opponent scored 4 goals in the match, but we do not know the number of goals that the MM club scored. Statement II is insufficient.
Considering both the statements we have following.

Thus, MM club could have won the match or could have tied. The question cannot be answered.
Hence, option (e).
Workspace:
Each question is followed by two statements, I and II. Answer each question using the following instructions:
Mark (1) if the question can be answered by using statement I alone but not by using statement II alone.
Mark (2) if the question can be answered by using statement II alone but not by using statement I alone.
Mark (3) if the question can be answered by using either of the statements alone.
Mark (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark (5) if the question cannot be answered by using any of the statements.
In a particular school, sixty students were athletes. Ten among them were also among the top academic performers. How many top academic performers were in the school?
I. Sixty per cent of the top academic performers were not athletes.
II. All the top academic performers were not necessarily athletes.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
- (e)
5
Answer: Option A
Text Explanation :
From Statement I, 40% of the top academic performers were athletes.
∴ If there are x top academic performers, 10 = 0.4x
∴ x = 25
Statement I is sufficient.
Statement II does not give any useful information.
Hence, option (a).
Workspace:
Each question is followed by two statements, I and II. Answer each question using the following instructions:
Mark (1) if the question can be answered by using statement I alone but not by using statement II alone.
Mark (2) if the question can be answered by using statement II alone but not by using statement I alone.
Mark (3) if the question can be answered by using either of the statements alone.
Mark (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark (5) if the question cannot be answered by using any of the statements.
Five students Atul, Bala, Chetan, Dev and Ernesto were the only ones who participated in a quiz contest. They were ranked based on their scores in the contest. Dev got a higher rank as compared to Ernesto, while Bala got a higher rank as compared to Chetan. Chetan’s rank was lower than the median. Who among the five got the highest rank?
I. Atul was the last rank holder.
II. Bala was not among the top two rank holders.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
- (e)
5
Answer: Option D
Text Explanation :
Chetan’s rank = 4 or 5
Now, Bala < Chetan and Dev < Ernesto.
From Statement I,

The highest rank holder cannot be determined. Statement I is insufficient.
Statement II is also insufficient.
Considering both statements together (refer to the table), Case 2 holds. Dev got the highest rank.
Hence, option (d).
Workspace:
Each question is followed by two statements, I and II. Answer each question using the following instructions:
Mark (1) if the question can be answered by using statement I alone but not by using statement II alone.
Mark (2) if the question can be answered by using statement II alone but not by using statement I alone.
Mark (3) if the question can be answered by using either of the statements alone.
Mark (4) if the question can be answered by using both the statements together but not by either of the statements alone.
Mark (5) if the question cannot be answered by using any of the statements.
Thirty percent of the employees of a call centre are males. Ten per cent of the female employees have an engineering background. What is the percentage of male employees with engineering background?
I. Twenty five per cent of the employees have engineering background.
II. Number of male employees having an engineering background is 20% more than the number of female employees having an engineering background.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
- (e)
5
Answer: Option C
Text Explanation :
Let there be 100x employees. So, 30x are male and 70x are female.
∴ 7x female employees have an engineering background.
From statement I, 25x employees have an engineering background.
∴ 18x male employees have an engineering background.
Required percentage = 18x × 100/ 30x
Statement I is sufficient.
From Statement II, Number of male employees having an engineering background = 1.2 × 7x
Required percentage = 1.2 × 7x × 100/30x
Hence, option (c).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
Ravi spent less than Rs.75 to buy one kilogram each of potato, onion, and gourd. Which one of the three vegetables bought was the costliest?
A. 2 kg potato and 1 kg gourd cost less than 1 kg potato and 2 kg gourd.
B. 1 kg potato and 2 kg onion together cost the same as 1 kg onion and 2 kg gourd.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option C
Text Explanation :
Let one kilogram of potatoes, onions and gourd cost Rs. p, Rs. o and Rs. g respectively. Then p + o + g < 75.
Consider statement A: 2p + g < p + 2g
∴ p < g
But, nothing is known about o.
∴ Statement A is insufficient.
Consider statement B: p + 2o = o + 2g
∴ o + p = 2g
∴ The cost of 1 kg of gourd is the average of the costs of 1 kg potatoes and 1 kg onions.
∴ g is neither the costliest nor the cheapest.
But the costliest vegetable cannot be found.
∴ Statement B is insufficient.
Considering both statements together: p < g and g is the average of p and o
∴ o > g
∴ Onions are the costliest.
Hence, option (c).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
Tarak is standing 2 steps to the left of a red mark and 3 steps to the right of a blue mark. He tosses a coin. If it comes up heads, he moves one step to the right; otherwise he moves one step to the left. He keeps doing this until he reaches one of the two marks, and then he stops. At which mark does he stop?
A. He stops after 21 coin tosses.
B. He obtains three more tails than heads.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option B
Text Explanation :
Let Tarak get h heads and t tails.
Let Tarak be at 0 on the number line.
Then the blue mark is at –3 and the red mark is at 2.
Consider statement A: h + t = 21 and
h – t = 2 (if he stops at the red mark) or
h – t = –3 (if he stops at the blue mark)
Solving, 2h = 23 (however, this is not possible)
or 2h = 18
∴ h = 9 and t = 12
∴ Tarak stops at the blue mark.
∴ Statement A is sufficient.
Consider statement B: h = t – 3 and h – t = 2 or h – t = –3
∴ He stops at the blue mark.
∴ Statement B is also sufficient.
Hence, option (b).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
Nandini paid for an article using currency notes of denominations Re. l, Rs. 2, Rs. 5, and Rs. 10 using at least one note of each denomination. The total number of five and ten rupee notes used was one more than the total number of one and two rupee notes used. What was the price of the article?
A. Nandini used a total of 13 currency notes.
B. The price of the article was a multiple of Rs. 10.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option D
Text Explanation :
Let Nandini use a, b, c and d notes of denominations 1, 2, 5 and 10 respectively.
Then c + d = a + b + 1 and price of the article = a + 2b + 5c + 10d
Consider statement A: a + b + c + d = 13
∴ 2(a + b) + 1 = 13
∴ a + b = 6, c + d = 7
Price of the article cannot be found from this data.
∴ Statement A is insufficient.
Consider statement B: a + 2b + 5c + 10d = 10k
As a, b, c, d ≥ 1, 10k ≥ 18
∴ k ≥ 2
But, statement B is also insufficient.
Considering both statements together: We know that a + b = 6, c + d = 7 and Price = 10k
When c = 2 and d = 5, Price = a + 2b + 60
When c = 4 and d = 3, Price = a + 2b + 50
Even if we assume that there is only one value of (a, b) such that a + 2b is a multiple of 10, we will still get at least 2 values for the price of the article.
Hence, data is insufficient.
Hence, option (d).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
Four candidates for an award obtain distinct scores in a test. Each of the four casts a vote to choose the winner of the award. The candidate who gets the largest number of votes wins the award. In case of a tie in the voting process, the candidate with the highest score wins the award. Who wins the award?
A. The candidates with the top three scores each vote for the top scorer amongst the other three.
B. The candidate with the lowest score votes for the player with the second highest score.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option A
Text Explanation :
Let A, B, C and D get the highest to lowest scores in that order.
Consider statement A: A votes for B, B votes for A and C votes for A.
If D votes for A, A wins.
If D votes for B, there is a tie between A and B and A wins as he has the highest score.
If D votes for C/D, A wins.
∴ Statement A alone is sufficient.
Consider statement B: D votes for B. This statement alone is not sufficient.
Hence, option (a).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
In a class of 30 students, Rashmi secured the third rank among the girls, while her brother Kumar studying in the same class secured the sixth rank in the whole class. Between the two, who had a better overall rank?
A. Kumar was among the top 25% of the boys merit list in the class in which 60% were boys.
B. There were three boys among the top five rank holders, and three girls among the top ten rank holders.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option A
Text Explanation :
Consider statement A: There were 60% of 30 = 18 boys in the class.
Kumar’s rank among boys ≤ |0.25 × 18| or 4
If Kumar’s rank among boys = 4, there are 2 girls in the first 6 rankers.
∴ Rashmi’s rank is seven.
If Kumar’s rank among boys is 3, 2 or 1, there are 3, 4 or 5 girls in the first 6 rankers.
∴ Rashmi’s rank is three.
∴ Statement A is insufficient.
Consider statement B: There were three boys in the top 5 and Kumar was 6th.
∴ There were 4 boys and 2 girls in the top 6.
∴ Rashmi was not in the top six.
∴ Kumar had a better overall rank.
Statement B is sufficient.
Hence, option (a).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
Zakib spends 30% of his income on his children’s education, 20% on recreation and 10% on healthcare. The corresponding percentages for Supriyo are 40%, 25%, and 13%. Who spends more on children’s education?
A. Zakib spends more on recreation than Supriyo.
B. Supriyo spends more on healthcare than Zakib.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option A
Text Explanation :
Let Zakib’s and Supriyo’s incomes be z and s respectively.
Consider statement A:
0.2z > 0.25s
∴ z > s
Zakib and Supriyo spend 0.3z and 0.4s on children’s education.
∴ Statement A alone is not sufficient.
Consider statement B:
0.13s > 0.1z
∴ Supriyo spends more than Zakib on children’s education.
∴ Statement B alone is sufficient.
Hence, option (a).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
Is a44 < b11, given that a = 2 and b is an integer?
- b is even
- b is greater than 16
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option A
Text Explanation :
a44 < b11
But, a = 2
∴ a44 = 244
∴ a44 = 1611
Using statement 1 alone:
b is an even integer. It may be less than or greater than 16.
So, we cannot answer the question using statement 1 alone.
Using statement 2 alone:
b is greater than 16.
∴ b11 > 1611
∴ b11 > a44
So, we can answer the question using statement 2 alone.
Hence, option (a).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
What are the unique values of b and c in the equation 4x2 + bx + c = 0 if one of the roots of the equation is (−1/2)?
A. The second root is 1/2
B. The ratio of c and b is 1
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option B
Text Explanation :
4x2 + bx + c = 0 …(i)
One root = −1/2
Using statement A alone:
Second root is 1/2.
Sum of the roots = −b/4 = (−1/2) + 1/2 = 0
∴ b = 0
Also, product of the roots = c/4 = (−1/2) × (1/2) = (−1/4)
∴ c = −1
So, statement A alone is sufficient to answer the question.
Using statement B alone:
Ratio of c and b is 1.
∴ b = c
∴ Equation (i) becomes 4x2 + bx + b = 0 ...(ii)
But one root = −1/2
Substituting x = −1/2 in the above equation (ii), we get,
1 − b/2 + b = 0
∴ b = −2 and c = −2
So, statement B alone is also sufficient to answer the question.
Hence, option (b).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
AB is a chord of a circle. AB = 5 cm. A tangent parallel to AB touches the minor arc AB at E. What is the radius of the circle?
A. AB is not a diameter of the circle
B. The distance between AB and the tangent at E is 5 cm
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option A
Text Explanation :
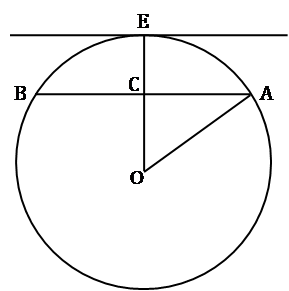
Let radius of circle be r.
AC = 2.5 as radius bisects the chord.
Using statement A alone:
We have been told that AB is not a diameter of the circle. But it does not give us any useful information to solve the problem.
So, statement A alone is not sufficient to answer the question.
Using statement B alone:
From the figure above, CE = 5
∴ OC = r − 5
∴ OA2 = OC2 + AC2
∴ r2 = (r − 5)2 + (2.5)2
Solving the above equation,
r = 3.125 cm
So, statement B alone is sufficient to answer the question.
Hence, option (a).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
Is
A. −3 ≤ a ≤ 3
B. One of the roots of the equation 4x2 − 4x + 1 = 0 is a
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option A
Text Explanation :
R.H.S. and L.H.S. are infinite GP's with common ratio = .
∴ We need to find whether
...(i)
This statement (i) is always true for a < 1.
Using statement A alone:
It does not give any conclusion regarding value of a i.e. whether it is less than 1 or not.
So, statement A alone is not sufficient to answer the question.
Using statement B alone:
4a2 − 4a + 1 = 0 …(ii)
∴ a = 1/2
So, statement B alone is sufficient to answer the question.
Hence, option (a).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
D, E, F are the mid-points of the sides AB, BC and CA of triangle ABC respectively. What is the area of DEF in square centimetres?
A. AD = 1 cm, DF = 1 cm and perimeter of DEF = 3 cm
B. Perimeter of ABC = 6 cm, AB = 2 cm, and AC = 2 cm
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option B
Text Explanation :
D, E and F are the midpoints of AB, BC and CA respectively.
Using statement A alone:
∵ AD = 1 cm
∴ BD = 1 cm …(Since D is the mid-point)
∵ DF = 1 cm
∴ BC = 2 cm …(Since D and F are the mid-points and DF is parallel to BC)
∴ BE = 1 cm and EC = 1 cm
∵ Perimeter of DEF = 3 cm
∴ EF = 1 cm
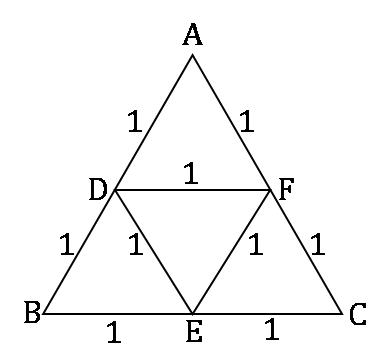
∴ Area of ∆DEF can be obtained.
So, statement A alone is sufficient to obtain the answer.
Using statement B alone:
∵ Perimeter of ∆ABC = 6 cm, AB = 2 cm, AC = 2 cm
∴ BC = 2 cm
∴ DE = 1, EF = 1 and DF = 1

So, statement B alone is also sufficient to obtain the answer.
Hence, option (b).
Workspace:
At the end of year 1998, Shepard bought nine dozen goats. Henceforth, every year he added p% of the goats at the beginning of the year and sold q% of the goats at the end of the year where p > 0 and q > 0. If Shepard had nine dozen goats at the end of year 2002, after making the sales for that year, which of the following is true?
- (a)
p = q
- (b)
p < q
- (c)
p > q
- (d)
p = q/2
Answer: Option C
Text Explanation :
Shepard bought 9 dozen goats at the end of 1998.
Consider that he added 1 dozen goats to it, i.e. 11.11% of 9 dozen.
And he sold 1 dozen to get back the same 9 dozen i.e. 10% of 10 dozen.
∴ He adds 11.11% and subtracts 10% to get the same amount every time.
∴ p = 11.11% and q = 10%
∴ p > q
Hence, option (c).
Workspace:
In each question there are two statements: A and B.
Choose 1 if the question can be answered by one of the statements alone but not by the other.
Choose 2 if the question can be answered by using either statement alone.
Choose 3 if the question can be answered by using both the statements together but cannot be answered using either statement alone.
Choose 4 if the question cannot be answered even by using both the statements A and B.
A game consists of tossing a coin successively. There is an entry fee of Rs. 10 and an additional fee of Re. 1 for each toss of the coin. The game is considered to have ended normally when the coin turns heads on two consecutive throws. In this case the player is paid Rs. 100. Alternatively, the player can choose to terminate the game prematurely after any of the tosses. Ram has incurred a loss of Rs. 50 by playing this game. How many times did he toss the coin?
A. The game ended normally.
B. The total number of tails obtained in the game was 138.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option B
Text Explanation :
Let the number of tosses be x.
Total amount spent by Ram after x tosses = (10 + x × 1) = Rs. (10 + x)
We know that Ram incurs a loss of Rs. 50.
∴ We have two cases to evaluate:
i. If the game ends normally then Ram's net loss = Rs. (10 + x) − Rs. 100
ii. If he quits prematurely his loss = Rs. (10 + x)
From statement A,
Ram's net loss = (10 + x) − 100
∴ 50 = (10 + x) − 100
∴ x = 140
∴ Statement A is alone sufficient.
From statement B,
Ram gets 138 tails.
If his game ends prematurely, his loss = 10 + x = 50
∴ x = 40
This is not possibe as the number of tails > 40
∴ His game must have ended normally.
∴ 10 + x – 100 = 50
∴ x = 140
∴ Statement B is also sufficient.
Hence, option (b).
Workspace:
In each question there are two statements: A and B.
Choose 1 if the question can be answered by one of the statements alone but not by the other.
Choose 2 if the question can be answered by using either statement alone.
Choose 3 if the question can be answered by using both the statements together but cannot be answered using either statement alone.
Choose 4 if the question cannot be answered even by using both the statements A and B.
Each packet of SOAP costs Rs. 10. Inside each packet is a gift coupon labelled with one of the letters S, O, A, and P. If a customer submits four such coupons that make up the word SOAP, the customer gets a free SOAP packet. Ms. X kept buying packet after packet of SOAP till she could get one set of coupons that formed the word SOAP. How many coupons with label P did she get in the above process?
A. The last label obtained by her was S and the total amount spent was Rs. 210.
B. The total number of vowels obtained was 18.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option C
Text Explanation :
From Statement A,
Number of soaps purchased by Ms. X = = 21
Also the last label obtained by her is S.
But this is not sufficient to get the number of P's.
∴ Statement A alone is not sufficient.
From Statement B,
The number of O's and A's is 18.
But this is also not individually sufficient to arrive at the required answer.
∴ Statement B alone is not sufficient.
After combining both the statements A and B, we can conclude that 18 out of 21 coupons are O's and A's and that the 21st is an S.
∴This means that the remaining two are P's.
Hence, option (c).
Workspace:
In each question there are two statements: A and B.
Choose 1 if the question can be answered by one of the statements alone but not by the other.
Choose 2 if the question can be answered by using either statement alone.
Choose 3 if the question can be answered by using both the statements together but cannot be answered using either statement alone.
Choose 4 if the question cannot be answered even by using both the statements A and B.
If A and B run a race, then A wins by 60 seconds. If B and C run the same race, then B wins by 30 seconds. Assuming that C maintains a uniform speed, what is the time taken by C to finish the race?
A. A and C run the same race and A wins by 375 metres.
B. The length of the race is 1 km.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option C
Text Explanation :
From the question, if A and C participate in a race, A will win by 90 seconds.
From statement A,
∵ A beats C by 375 m or 90 sec.
∴ C's speed =
But the length of the track is not known.
∴ Statement A is not sufficient to find the time taken by C to complete the race.
From Statement B we cannot find the speed of C.
∴ Statement B alone is not sufficient.
After combining both the statements A and B, the time taken by C to complete the race
= 240 sec
Hence, option (c).
Workspace:
Choose 1, if the question can be answered by using statement A alone but not by using B alone.
Choose 2, if the question can be answered by using statement B alone but not by using A alone.
Choose 3, if the question can be answered by using either statement alone.
Choose 4, if the question can be answered by using both the statements together but not by either statement.
In a cricket match, the ‘man of the match’ award is given to the player scoring the highest number of runs. In case of a tie, the player (out of those locked in the tie) who has taken the higher number of catches is chosen. Even thereafter if there is a tie, the player (out of those locked in the tie) who has dropped fewer catches is selected. Aakash, Biplab and Chirag who were contenders for the award dropped at least one catch each. Biplab dropped 2 catches more than Aakash did, scored 50, and took 2 catches. Chirag got two chances to catch and dropped both. Who was the ‘man of the match’?
A. Chirag made 15 runs less than both Aakash and Biplab.
B. The catches dropped by Biplab are 1 more than the catches taken by Aakash.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option D
Text Explanation :

From Statement A
We get the table as shown above :
∵ We do not know the number of catches taken by Aakash.
∴ Statement A alone is not sufficient.
Statement B does not give any information about the runs scored.
∴ Statement B alone is not sufficient.
After combining both the statements, we get,
Number of catches taken by Aakash = x + 1
∴ If x = 1 then Aakash is man of the match since he has dropped fewer catches.
If x > 1 then Aakash will be the man of the match as he has taken more catches.
Hence, option (d).
Workspace:
Four friends, A, B, C and D got the top four ranks in a competitive examination, but A did not get the first, B did not get the second, C did not get the third, and D did not get the fourth rank. Who secured which rank?
A. Neither A nor D were among the first 2.
B. Neither B nor C was third or fourth.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option C
Text Explanation :
From statement A,
Neither A nor D were among the first 2 which means that D gets either 3rd or the 4th rank.
∵ D did not get the 4th rank.
∴ D gets the 3rd rank and A gets the 4th rank.
∵ B didn’t get the 2nd rank.
∴ B gets the 1st rank and C gets the 2nd rank.
∴ Statement A alone is sufficient.
From statement B,
B gets either the 1st or the 2nd rank.
We know that B did not get the 2nd rank.
∴ B gets the 1st rank and C gets the 2nd rank.
∵ D didn’t get the 4th rank.
∴ D gets the 3rd rank and A gets 4th rank.
∴ Statement B alone is sufficient.
∴ The question can be answered using either statements alone.
Hence, option (c).
Workspace:
The members of a local club contributed equally to pay Rs.600 towards a donation. How much did each one pay?
A. If there had been five fewer members, each one would have paid an additional Rs.10.
B. There were at least 20 members in the club, and each one paid no more than Rs.30.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option A
Text Explanation :
From statement A,
Let there are x members in the club.
∴ x = 20
∴ Contribution per head = = Rs. 30
∴ Statement A alone is sufficient.
From statement B,
We get there were at least 20 members in the club and each one paid no more than Rs. 30.
The different possibilities for can be :
30 members × 20 rupees = Rs. 600
40 members × 15 rupees = Rs. 600
60 members × 10 rupees = Rs. 600 and so on.
∴ Statement B alone is not sufficient.
Hence, option (a).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report