Geometry - Quadrilaterals & Polygons - Previous Year CAT/MBA Questions

Answer: Option A

Text Explanation :

Answer: Option C

Text Explanation :

Answer: Option D

Video Explanation

Text Explanation :

​​​​​​​​​​​​​​

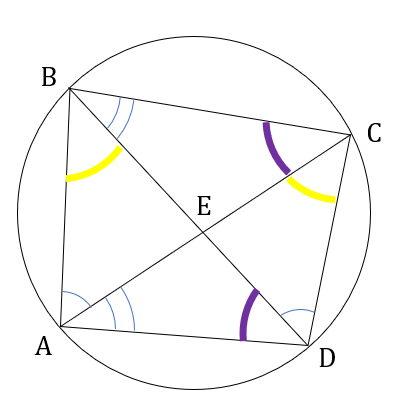
∠DAC = ∠DBC [angle subtended in same segment by same chord are equal]
Similarly,
∠ADB = ∠ACB
∠CDB = ∠CAB
∠ACD = ∠ABD

∆AED is similar to ∆BEC
[∠DAC = ∠DBC and ∠ADB = ∠ACB]
∴ $\frac{\mathrm{ED}}{\mathrm{EC}}$ = $\frac{\mathrm{AD}}{\mathrm{BC}}$ = $\frac{4}{5}$   ...(1)

∆AEB is similar to ∆DEC
[∠CDB = ∠CAB and ∠ACD = ∠ABD]
∴ $\frac{\mathrm{AE}}{\mathrm{ED}}$ = $\frac{\mathrm{AB}}{\mathrm{CD}}$ = $\frac{2}{1}$   ...(2)

(1) × (2)
⇒$\frac{\mathrm{ED}}{\mathrm{EC}}\times \frac{\mathrm{AE}}{\mathrm{ED}}$ = $\frac{4}{5}\times \frac{2}{1}$ = $\frac{8}{5}$

Hence, option (d).

Concept:

Angle subtended in same segment of a circle by same chord are equal

Answer: Option A

Video Explanation

Text Explanation :

​​​​​​​

Area of △ABP, △APQ and AQCD are in GP.
Let their areas be A, Ar and Ar² 
Now, Area of AQCD = 4 × Area of △ABP
⇒ Ar² = 4 × A
⇒ r = 2

∴ Area of △ABP : Area of △APQ : Area of AQCD = 1 : 2 : 4

From the figure given above
Area of △ABP = 1/2 × BP × AB = 1/2 × BP × 9 = 4.5 × BP
Area of △APQ = 1/2 × PQ × AB = 1/2 × PQ × 9 = 4.5 × PQ
Area of AQCD = 1/2 × (QC + AD) × AB = 1/2 × (QC + 6) × 9 = 4.5 × (QC + 6)

Now, Area of △APQ = 2 × Area of △ABP
⇒ 4.5 × PQ = 2 × 4.5 × BP
⇒ PQ = 2BP

∴ QC = 6 - BP - PQ = 6 - 3BP

Now, Area of AQCD = 4 × Area of △ABP
⇒ 4.5 × (QC + 6) = 4 × 4.5 × BP
⇒ 4.5 × (6 - 3BP + 6) = 4 × 4.5 × BP
⇒ 6 - 3BP + 6 = 4BP
⇒ BP = 12/7

∴ PQ = 24/7 and

∴ QC = 6 - 3 × 12/7 = 6/7

⇒ BP : PQ : QC = 12/7 : 24/7 : 6/7 = 2 : 4 : 1

Hence, option (a).

Answer: Option A

Video Explanation

Text Explanation :

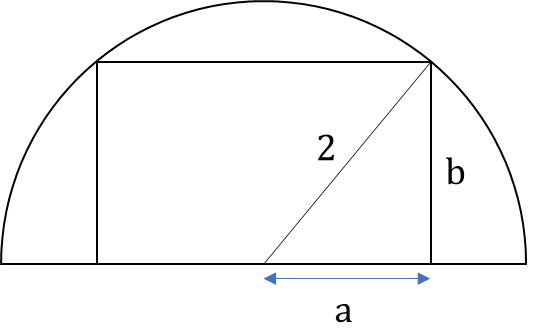
Let the longer side of the rectangle is 2a and the shorter side is b as shown in the figure.

Using pythagoras theorem, we get
a² + b² = 2² = 4   ...(1)

Also, AM ≥ GM
⇒ $\frac{{\mathrm{a}}^2+{\mathrm{b}}^2}{2}$ ≥ $\sqrt{{\mathrm{a}}^2{\mathrm{b}}^2}$

⇒ a² + b² ≥ 2ab

⇒ 4 ≥ 2ab

⇒ 2 ≥ ab

∴ Highest value of ab = 2, when a = b.

⇒ Ratio of longer side to shorter side = 2a : b = 2 : 1.

Hence, option (a).

Answer: 54

Video Explanation

Text Explanation :

Let the exterior angle be x°, hence interior angle is (x + 120)°.

Sum of interior and exterior angles is 180°.
⇒ x + (x + 120) = 180
⇒ x = 30°

∴ Interior angle of this regular polygon = 30 + 120 = 150°

Each interior angle of a regular polygon of n sides = (n - 2)/n × 180° = 150°
⇒ (n - 2)/n = 5/6
⇒ n = 12

Now, number of diagonals in a n-sided polygon = n × (n - 3)/2 = 12 × 9/2 = 54

Hence, 54.

Answer: 66

Video Explanation

Text Explanation :

Let AB = x

​​​​​​​

In right ∆CED,CE = AB = x
⇒ CD = $\sqrt{{\mathrm{x}}^2+25}$

In the given figure,
⇒ 3 + 8 + x + $\sqrt{{\mathrm{x}}^2+25}$ = 36
⇒ $\sqrt{{\mathrm{x}}^2+25}$ = 25 – x
⇒ x² + 25 = 625 + x² – 50x
⇒ 50x = 600
⇒ x = 12

Now, area of a trapezium = 1/2 × (sum of parallel sides) × height
= 1/2 × 11 × 12 = 66

Hence, 66.

Answer: 10

Video Explanation

Text Explanation :

Interior angle of a n-sided regular polygon = $\frac{(n-2)\times 180°}{n}$

Let the number of sides of polygon A and B be n and 2n respectively.

⇒ $\frac{{\displaystyle \frac{(n-2)\times 180°}{n}}}{{\displaystyle \frac{(2n-2)\times 180°}{2n}}}$ = $\frac{3}{4}$

⇒ $\frac{n-2}{n-1}$ = $\frac{3}{4}$

⇒ 4n – 8 = 3n – 3

⇒ n = 5

∴ Number of sides of polygon B = 2n= 10.

Hence, 10.

Answer: Option A

Video Explanation

Text Explanation :

In a quadrilateral, the longest side is less than the sum of other three sides and greater than the least of the difference of any 2 of the other three sides.

Let the fourthe sides of the quadrilateral be x.

⇒ 2 - 1 < x < 1 + 2 + 4
⇒ 1 < x < 7
∴ x can be 2, 3, 4, 5 or 6

Hence, x can take 5 integral values.

Hence, option (a).

Answer: Option C

Video Explanation

Text Explanation :

Side of the regular hexagon = 2 cm.
Consider the figure below.

​​​​​​​

Consider the isosceles ∆ATF

TU is the altitude from T to AF. 
We know, in a regular hexagon the distance between any two parallel sides = √3 × side.
∴ TU = √3 × 2 = 2√3 cm.

Since ATF is an isosceles triangle, U will be the mid-point of AF
∴ AU = 1 cm.

In ∆ATU
AT² = TU² + AU²
⇒ AT² = (2√3)² + 1²
⇒ AT² = 13
⇒ AT = √13

Hence, option (c).

Answer: Option B

Video Explanation

Text Explanation :

Refer the diagram below.

​​​​​​​

ABPD is a parallelogram.

ABPD and ∆BPC have equal base and same height.

∴ Area (ABPD) = 2 × Area (∆BPC)

Also, Area (ABPD) - Area (∆BPC) = 10

⇒ 2 × Area (∆BPC) - Area (∆BPC) = 10

⇒ Area (∆BPC) = 10

∴ Area (ABPD) = 20

⇒ Area (ABCD) = Area (ABPD) + Area (∆BPC) = 20 + 10 = 30

Hence, option (b).

Answer: Option B

Video Explanation

Text Explanation :

Consider the diagram below.

​​​​​​​

In a rhombus diagonals perpendicularly bisect each other.

∴ Let OA = OC = x and OB = OD = y

In ∆AOB ⇒ x² + y² = 5²  …(1)

Also, area of the rhombus = ½ × 2x × 2y = 12

⇒ 2xy = 12   …(2)

(1) + (2)
⇒ x² + y² + 2xy = 25 + 12 = 37
⇒ (x + y)² = 37
⇒ x + y = √37   …(3)

(1) - (2)
⇒ x² + y² - 2xy = 25 - 12 = 13
⇒ (x - y)² = 13
⇒ x - y = √13   …(4)

Solving (3) and (4) we get,

2x = √37 + √13 and
2y = √37 - √13

∴ The longer diagonal = 2x = √37 + √13

Hence, option (b).

Answer: 3500

Video Explanation

Text Explanation :

Side of the rhombus = ¼ × 40 = 10 cm.

Area of a rhombus = ½ d₁d₂ = 96 [d₁ and d₂ are the two diagonals]

⇒ d₁d₂ = 192

We know, (d₁/2)² + (d₂/2)² = 10²

⇒ d₁² + d₂² = 400

⇒ (d₁ + d₂)² - 2d₁d₂ = 400

⇒ (d₁ + d₂)² – 2 × 192 = 400

⇒ (d₁ + d₂)² = 784

⇒ d₁ + d₂ = 28

Hence, the cost of laying electric wore along its two diagonals = 125 × (d₁ + d₂) = 125 × 28 = Rs. 3,500

Hence, 3500.

Answer: Option C

Video Explanation

Text Explanation :

​​​​​​​

Let AE be a perpendicular from A to DC.

∆ADE is a 30-60-90 triangle.
⇒ DE = √3/2 × 10 = 5√3
⇒ AE = 10/2 = 5

∆ACE is a right triangle.
⇒ CE² = AC² – AE²
⇒ CE² = 400 – 25 = 375
⇒ CE = 5√15

∴ Area of parallelogram = 2 × Area of triangle ADC
⇒ Area of parallelogram = 2 × (1/2 × CD × AE) = CD × AE
= (DE + EC) × AE
= (5√3 + 5√15) × 5
= 25(√3 + √15)

Hence, option (c).

Answer: Option D

Video Explanation

Text Explanation :

The following diagram can be drawn from the given information.

​​​​​​​

⇒ Area of the Rhombus = $\frac{1}{2}\times 12\times 16$ = 96

Radius of the circle is same as the height of ∆ABC

In a right triangle, altitude from right angle = $\frac{Product of shorter sides}{hypotenuese}$ = $\frac{\left(6\times 8\right)}{10}$ = $\frac{24}{5}$

⇒ Area of circle = $\pi {\left(\frac{24}{5}\right)}^2$

∴ Area of Circle : Area of Rhombus = $\pi {\left(\frac{24}{5}\right)}^2 : 96$ = 6π : 25.

Hence, option (d).

Answer: Option A

Video Explanation

Text Explanation :

Let the side of equilateral triangle be a. Hence, perimeter = 3a.

Let the sides of the rectangle be x and 3x. Hence, perimeter = 8x

Given, 3a + 8x = 90   …(1)

Also given, R = T²

⇒ x × 3x = ${\left[\frac{\sqrt{3}}{4}{a}^2\right]}^2$

⇒ 16x² = a⁴

⇒ a² = 4x

Substituting x in (1)

⇒ 3a + 2a² = 90

⇒ 2a² + 3a – 90 = 0

⇒ a = -15/2 or 6 (-ve value will be rejected) 

∴ x = $\frac{a^2}{4}$ = 9

∴ Longer side of the rectangle = 3x = 27.

Hence, option (a).

Answer: 28

Video Explanation

Text Explanation :

The following diagram can be drawn using the information given.

​​​​​​​

Since, ∆ADE is an isosceles right triangle hence, DE = AE = 4 cm

⇒ AB = BE + AE = 5 + 4 = 9 cm

∴ Area of trapezium = $\frac{1}{2}\times (CD+AB)\times BC$ = $\frac{1}{2}\times 14\times 4$ = 28 cm².

Hence, 28.

Answer: 150

Video Explanation

Text Explanation :

Sum of the interior angles of a n-sided Polygon = (n - 2) × 180

Measure of each interior angle = $\frac{(n-2)}{n}$× 180°

So, Interior angle of the polygon with side a = $\frac{(a-2)}{a}$ × 180°

Interior angle of the polygon with side b = $\frac{(2a-2)}{2a}$ × 180°

It is given that interior angle of side b is 3/2 times to that of the polygon with side A

⇒ $\frac{(2a-2)}{2a}$ × 180° =  $\frac{3}{2}\left[\frac{(a-2)}{a}\times 180°\right]$

⇒ (2a - 2) × 180 = (3a - 6) × 180

⇒ 2a - 2 = 3a - 6

⇒ a = 4. So, b = 8

Now, (a + b) sides = 8 + 4 = 12 sides

Interior angle =$\frac{12-2}{12}$× 180° = 150°

Hence, 150.

Answer: Option D

Video Explanation

Text Explanation :

y > x

Side of smaller square = $\sqrt{x^2+y^2}$
∴ Area of smaller square = (x² + y²)

Side of bigger square = (x + y)
∴ Area of bigger square = (x + y)²

By the given condition,

⇒ x² + y² = 62.5% of (x + y)²

⇒ x² + y² = 5/8 (x + y)²

⇒ 8x² + 8y² = 5x² + 5y² + 10xy

⇒ 3x² + 3y² - 10xy = 0

⇒ 3${\left(\frac{x}{y}\right)}^2$ -10$\left(\frac{x}{y}\right)$ + 3 = 0

⇒ $\left(\frac{x}{y}\right)$ = $\frac{10\pm \sqrt{{10}^2-4\times 3\times 3}}{6}$ = $\frac{10\pm 8}{6}$ = 9/3 of 1/3

As y > x, x/y < 1

∴ x : y = 1 : 3

Hence, option (d).

Answer: Option D

Video Explanation

Text Explanation :

Area of parallelogram = base × height
∴ A(□ABCD) = CD × AP
∴ 72 = 9 × AP
∴ AP = 8

Consider ∆APD.

PD = $\sqrt{{16}^2-8^2}$ = 8√3

A(APD) = 1/2 × 8√3 × 8 = 32√3 sq.cm.

Hence, option (d).

Answer: Option B

Video Explanation

Text Explanation :

As □ABCD is a rectangle, diagonal AC will be the diameter of the circle

∴ AC = DB = 2 × 13 = 26 cm

⇒ AB² + BC² = 26² = 676

Only option (b) satisfies this: (24² + 10²) = 676

Hence, option (b).

Answer: Option B

Video Explanation

Text Explanation :

 
Area of parallelogram = Base × Height

∴ 48 = 8 × Height

∴ Height = 6 cm

If the parallelogram is a rectangle, AD is its height. In that case, s = 6.

Otherwise, using Pythagoras theorem, AD > 6 or s > 6.

Therefore, s ≥ 6.

Hence, option (b).

Answer: Option C

Video Explanation

Text Explanation :

Suppose l = length of the rectangle and b = breadth of the rectangle.

Therefore, the area of the rectangle = lb and the perimeter of the rectangle = 2(l + b)

Therefore,

$\frac{\mathcal{l}b}{{\left[2\right(l+b\left)\right]}^2}=\frac{1}{25} i.e. \frac{\iota b}{{(l+b)}^2}=\frac{4}{25}$

Substituting the options, we can see that only option (c) i.e., 1 : 4 matches.

Hence, option (c).

Answer: Option B

Video Explanation

Text Explanation :

ABCDEF is a hexagon with side 1 cm. Let us construct the diagram as shown below

Now if we look at triangle ABC 

Further, as AB = BC, △ABC will become a 120° - 30° - 30° triangle and the ratio of it’s sides. (∵ ∠ABC is an angle of regular hexagon ABCDEF)

will be √3 : 1 : 1.

Now $\frac{AC}{AB}=\frac{\sqrt{3}}{1}$

∴ AC = √3 units

Area of square with side AC = (√3)² = 3 sq.units

Hence, option (b).

Answer: 90

Video Explanation

Text Explanation :

​​​​​​​

Angle subtended by an arc on circle is half of the angle it makes at the center.
∴​​​​​​​ Considering arc CD, it makes an angle of 120° at the center hence ∠CAD = 60°.

⇒ ∠BAD = 90°

Now, in a cyclic quadrilateral, sum of opposite angle = 90°.

⇒ ∠BAD + ∠BCD = 90°
∴ ∠BCD = 90°

Hence, 90.