Concept: Calculating Squares
CONTENTS
- Remember
- Squares of numbers from 26 to 75
- Squares of numbers from 76 to 125
- Squares of numbers ending in 5
Square of numbers from 1 to 25.
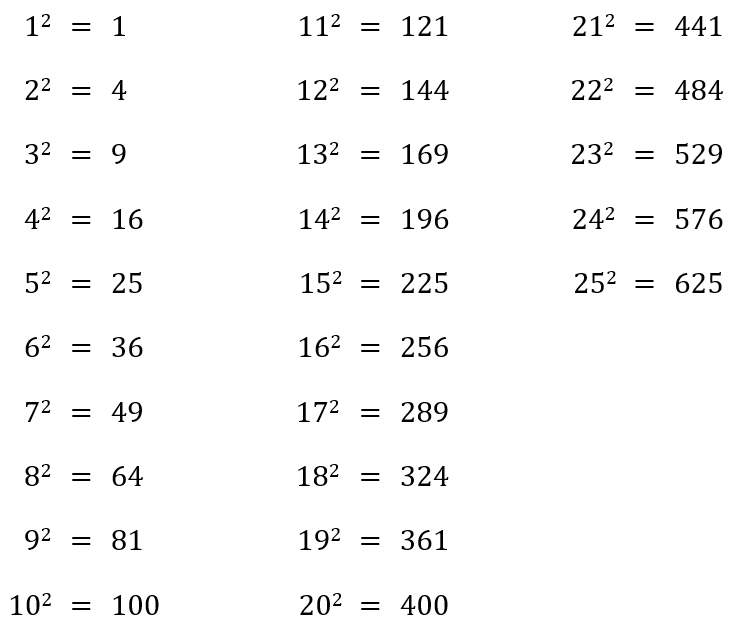
- Last digit of a perfect square will always be 1 or 4 or 5 or 6 or 9 or 0, i.e., last digit cannot be 2, 3, 7 & 8.
- For a perfect square, if the unit's digit is not 6, the ten's digit will always be even.
- For a perfect square, if the unit's digit is equal to 6, the ten's digit will always be odd.
- The last 2 digits of a perfect square will be last two digits of 12 or 22 or 32 or ... or 252.
- The square of a number with only 1’s will always be a palindrome. Example: 112 = 121; 1112 = 12321; 11112 = 1234321.
If we want to calculate square of N (where N is from 26 till 75), we first write it as 50 + x or 50 - x.
Now, calculate x2. Right most 2 digits of N2 will be same as right most two digits of x2 and any part of x2 left will be carried forward.
Left part of N2 will be equal to 25 + x or 25 - x.

Example : Calculate square of 37.
Solution :
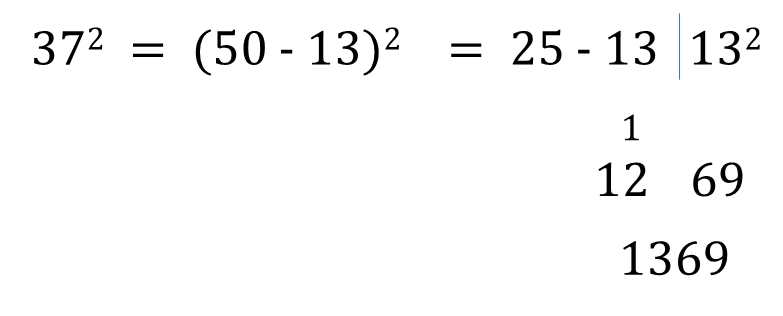
Example : Calculate square of 59.
Solution :
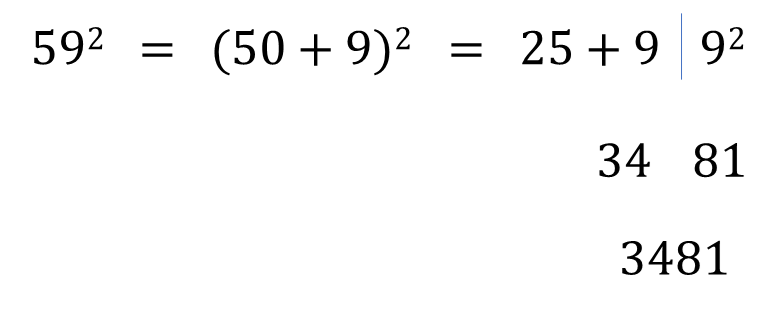
If we want to calculate square of N (where N is from 76 till 125), we first write it as 100 + x or 100 - x.
Now, calculate x2. Right most 2 digits of N2 will be same as right most two digits of x2 and any part of x2 left will be carried forward.
Left part of N2 will be equal to N + x or N - x.

Example : Calculate square of 87.
Solution :
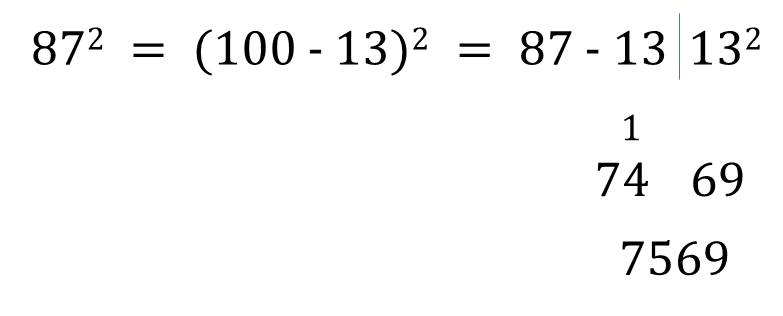
Example : Calculate square of 109.
Solution :
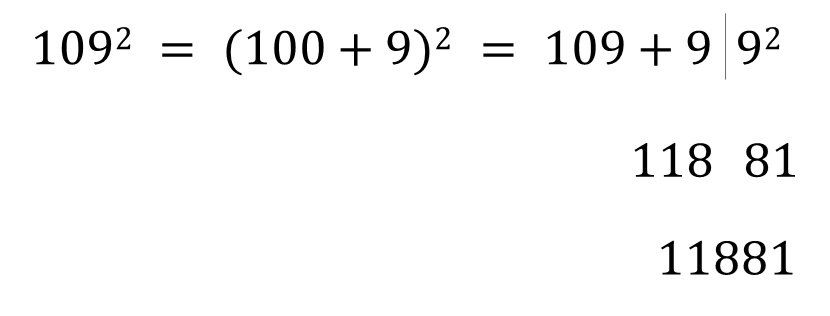
Consider a number of the form 'a5', where 5 is the unit's digit and a is the number left after removing 5.
Now, (a5)2 consists of two partns
- last two digits of (a5)2 will always be 25.
- left part of the answer = a × (a + 1).
Example : Calculate square of 105.
Solution :
Last two digits of 1052 = 25.
Left part of the answer = 10 × 11 = 110.
∴ 1052 = 11025.
- Last two digits of (50 ± x)2 = last two digits of x2.
- Last two digits of (100 ± x)2 = last two digits of x2.
Example: Find the last two digits of 1132 + 8972 + 5612 + 892.
Solution:
Last two digits of (1132 + 8972 + 5612 + 892)
= last two digits of (132 + 972 + 612 + 892)
= last two digits of (132 + 32 + 112 + 112)
= last two digits of (69 + 9 + 21 + 21) = 20.
Example: Which of the following is a perfect square?
(a) 2343 (b) 3562
(c) 5687 (d) 2209
Solution:
A perfect square never ends in 2, 3, 7 or 8, hence options (a), (b) & (c) are rejected.
∴ Option (d) is a perfect square. It is square of 47.
Example: Which of the following is not a perfect square?
(a) 4489 (b) 9604
(c) 3249 (d) 8648
Solution:
A perfect square never ends in 2, 3, 7 or 8.
∴ Option (d) cannot be a perfect square.
Example: If x is a natural number such that 1 < x < 200 & the last 2 digits of x2 are 89. How many values of x are possible?
Solution:
Least number whose square ends in 89 is 17.
Next number whoes square ends in 89 will be 50 - 17 = 33.
Next number whoes square ends in 89 will be 50 + 17 = 67.
Next number whoes square ends in 89 will be 100 - 17 = 83.
Next number whoes square ends in 89 will be 100 + 17 = 117.
Next number whoes square ends in 89 will be 150 - 17 = 133.
Next number whoes square ends in 89 will be 150 + 17 = 167.
Next number whoes square ends in 89 will be 200 - 17 = 183.
∴ 8 such numbers are there.