CRE 3 - Circles | Geometry, Mensuration & Trigonometry
What is the diameter (in cm) of a circle with area 36π cm2?
- A.
20 cm
- B.
12.5 cm
- C.
12 cm
- D.
6 cm
Answer: Option C
Explanation :
Area of the circle, A = πr2 = 36π
⇒ r2 = 36
∴ Radius, r = 5 cm
∴ Diameter, d = 2 × 5 = 12 cm
Hence, option (c).
Workspace:
What is the circumference (in cm2) of a circle for which the ratio of the area and the circumference is 7 : 4? [Take π = 22/7]
- A.
44 cm
- B.
22 cm
- C.
15π cm
- D.
7π/2 cm
Answer: Option B
Explanation :
Ratio of area and circumference of a circle = πr2 : 2πr = r : 2
∴ 7/4 = r/2
∴ r = 7/2 cm
∴ Circumference of the circle = 2πr = 2 × 22/7 × 7/2 = 22 cm.
Hence, option (b).
Workspace:
What is the area (in cm2) and the perimeter (in cm) of a quarter circle with radius 14 cm? [Take π = 22/7]
- A.
154, 50
- B.
98π, 50
- C.
49π, 22π
- D.
49π, 2π
Answer: Option A
Explanation :
A quarter circle can be considered as a sector with θ = 90° as shown below.
Hence, the area of the quarter circle has to be equal to the area of the sector and the perimeter has to be the same as the perimeter of the sector.

Area of sector O-ACB = 1/4 × area of circle = 1/4 × πr2 = 1/4 × 22/7 × 14 × 14 = 154 cm2
Perimeter of sector O-ACB = length(arc ACB) + length(OA) + length(OB)
= + r + r = + 14 + 14 = 50 cm.
Hence, option (a).
Workspace:
What is the length of a chord which is at a distance of 6 cm from the center of a circle with radius 10 cm?
- A.
12 cm
- B.
16 cm
- C.
24 cm
- D.
18 cm
Answer: Option B
Explanation :

A perpendicular drawn from the center of the circle to the chord bisects the chord.
In the above figure, OD bisects chord AB i.e. AD = DB
In ∆ODB, ∠ODB = 90°
Using Pythagoras theorem, we get,
OB2 = DB2 + OD2
∴ 102 = DB2 + 62
∴ DB2 = 100 – 36 = 64
∴ DB = 8 cm
Length of chord AB = 2 × DB = 2 × 8 = 16 cm
Hence, option (b).
Workspace:
A chord subtends an angle of 100° at the center of a circle. What is the angle subtended by the chord in the major segment of the circle?
- A.
80°
- B.
160°
- C.
50°
- D.
260°
Answer: Option C
Explanation :

The angle subtended by a chord on a point on the circumference (which lies in the major segment) of the circle measures half the angle subtended by the same chord at the center.
In the above figure, chord AC subtends an angle ∠ADB at point D lying on the major arc and an angle ∠AOB at the center of the circle.
∴ m ∠AOB = 2 × m ∠ADB
m ∠AOB = 100°
∴ m ∠ADB = 50°
∴ The angle subtended by the chord AB in the major segment = 50°
Hence, option (c).
Workspace:
In the given circle with center O, AB and CD are two chords that intersect at point X. DX = 6 cm, CX = 8 cm, and BX = 4 cm. What is the radius of the circle?

- A.
12 cm
- B.
10 cm
- C.
8 cm
- D.
Can't be determined
Answer: Option C
Explanation :
If two chords intersect internally as shown in the figure,
DX × CX = AX × BX;
∴ AX = (6 × 8)/4 = 12 cm
AB = AX + BX = 12 + 4 = 16 cm
AB is the diameter of the circle.
∴ Radius AO = 16/2 = 8 cm
Hence, option (c).
Workspace:
A truck has wheels of diameter 1.4 m. How many times must a wheel of the truck rotate to cover a distance of 1.1 km?
- A.
210
- B.
200
- C.
250
- D.
None of these
Answer: Option C
Explanation :
Circumference of a wheel = (22/7) × 1.4 = 4.4 m
∴ Total number of rotations = (1100/4.4) = 250 rotations
Hence, option (c).
Workspace:
What is the circumference of a circle whose area is equal to that of an equilateral triangle with perimeter P?
- A.
- B.
- C.
√3 P
- D.
Answer: Option D
Explanation :
Perimeter of the equilateral triangle = P
∴ Side of the equilateral triangle = P/3
∴ The area of the equilateral triangle =
But the area of the equilateral triangle is equal to the area of the circle.
Area of the circle = πr2 =
∴ Radius of the circle, r =
∴ The circumference of the circle = 2πr =
Hence, option (d).
Workspace:
Radius of two smaller semicircles shown in the figure is 2 cm. What is the area (in cm2) of the shaded portion bounded by three semicircles as shown in the figure?

- A.
8π
- B.
16π - 1
- C.
8π - 1
- D.
None of these
Answer: Option A
Explanation :

The three semicircles in the figure can be named S1, S2 and S3 as shown above.
Since the two semicircles have equal radii, their area also has to be equal to each other.
Area(S2) = Area(S3)
Hence, we can redraw the figure like this.

Area of the shaded portion is same as the area of S1.
Radius of S1 = 4.
∴ Area of shaded portion = ½ × π × 4 × 4 = 8π
Hence, option (a).
Workspace:
In the given figure, O is the center of the circle. The sum of angles a and b is:

- A.
50°
- B.
100°
- C.
25°
- D.
Can't be determined
- E.
None of these
Answer: Option C
Explanation :

Join OR as shown.
m ∠ORP = m ∠OPR = a …(OP = OR; ∆ORP is isosceles)
Similarly, m ∠ORQ = m ∠OQR = b …(OQ = OR, ∆ORQ is isosceles)
m ∠PRQ = a + b
Now, m ∠PRQ × 2 = m ∠POQ
∴ m ∠PRQ = 25°
∴ a + b = 25°
Hence, option (c).
Workspace:
In the given figure, QR is the diameter of the circle. P and S are points on the circle such that ∠RPS = 50°. Find ∠SRQ.

- A.
30°
- B.
40°
- C.
50°
- D.
60°
Answer: Option B
Explanation :

Given QR is the diameter. Let QS be a chord.
Diameter subtends an angle 90° anywhere on the circle
∴ ∠RPQ = 90°.
Given, ∠RPS = 50°.
⇒ ∠SPQ = 90° - 50° = 40°.
Also, a chord subtends same angle in the same segment of the circle.
∴ ∠SRQ = ∠SPQ = 40°
Hence, option (b).
Workspace:
What is the distance in cm between two parallel chords of length 16 cm and 12 cm in a circle of radius 10 cm?
- A.
15
- B.
18
- C.
14
- D.
None of these
Answer: Option C
Explanation :
We can draw the following diagram from the infomation given.

The perpendicular drawn on a chord from the center of the circle bisects the chord
⇒ BX = 16/2 = 8 and
⇒ DY = 12/2 = 6 and
Now, in ∆BOX
⇒ BO2 = BX2 + OX2
⇒ 102 = 82 + OX2
⇒ OX = 6
Also, in ∆BOX
⇒ DO2 = DY2 + OY2
⇒ 102 = 62 + OY2
⇒ OY = 8
XY = OX + OY = 6 + 8 = 14
Hence, option (c).
Workspace:
In the figure AB and CD are two diameters of the circle intersecting such that ∠COB = 50°. E is any point on arc CB. Find ∠CEB?

- A.
165°
- B.
155°
- C.
145°
- D.
100°
Answer: Option B
Explanation :
∠COB = ∠AOD = 50°
⇒ ∠CDB = 25° [Angle subtended by a chord on circle in same segment is half of the angle it subtends on the center.]

Now, angle subtended by a chord in opposite segments are complementary. If we consider the chord CB, then
⇒ ∠CDB + ∠CEB = 180°
⇒ ∠CEB = 180° - 25° = 155°
Hence, option (b).
Workspace:
In the adjoining figure, chord ED is parallel to the diameter AC of the circle. If angle CBE = 45°, then what is the value of angle DEC?

- A.
45°
- B.
65°
- C.
55°
- D.
30°
- E.
None of these
Answer: Option A
Explanation :
In the given figure if we join AB then ∠ABC = 90°. [Angle subtended by diameter AC on circle is right angle.]
∴ ∠ABE + ∠EBC = 90°
⇒ ∠ABE = 90° - 45° = 45°
Now, if we consider chord AE, angle it subtends at point B on circle will be same as the angle it subtends at point C on the circle.
⇒ ∠ABE = ∠ACE = 45°
Now, AC and ED are parallel
⇒ ∠ACE = ∠CED = 45° [alternate interior angles]

Hence, option (a).
Workspace:
Two chords AB and CD of circle whose centre is O, meet at the point P inside the circle such that ∠AOC = 50°, ∠BOD = 40°. Then the value of ∠BPD is
- A.
60°
- B.
40°
- C.
45°
- D.
75°
Answer: Option C
Explanation :
Let us join BC.

Now, ∠ABC = ½∠AOC = 25° (angle subtended by chord AC on circle is half of the angle it subtends at the center)
similalry, ∠DCB = ½∠DOB = 20° (angle subtended by chord AC on circle is half of the angle it subtends at the center)
In triangle, BPC, ∠BPD = ∠PCB + ∠PBC (exterior angle is sum of two opposite interior angles)
⇒ ∠BPD = 25° + 20° = 45°
Hence, option (c).
Workspace:
In the figure given below, O is the center of the circle and ∠PQR = 100° and ∠STR = 105°. What is the value (in degrees) of ∠SOP?

- A.
80
- B.
45
- C.
65
- D.
50
Answer: Option D
Explanation :
Let us join S and R with point X as shown in the figure.

∠SAR = 180° - ∠STR = 180° - 105° = 75°
∠SOR = 2∠SAR = 150°
Now, ∠OSR + ∠ORS + ∠SOR = 180°
⇒ ∠OSR + ∠OSR + 150° = 180° (∠OSR = ∠ORS )
⇒ ∠OSR = 15° ...(1)
Also, RQRS is a cyclic quadratilateral, hence two opposite angles are supplementary
⇒ ∠PSR + ∠PQR = 180°
⇒ ∠PSR + 100° = 180°
⇒ ∠PSR = 80° ...(2)
From (1) and (2)
∠PSO = 80° - 15° = 65°
In ∆POS
⇒ ∠PSO + ∠SPO + ∠POS = 180°
⇒ 65° + 65° + ∠POS = 180° (∠PSO = ∠SPO)
⇒ ∠POS = 50°
Hence, option (d).
Workspace:
Two chords AB and CD of a circle intersect at a point P, which lies outside the circle. If PA = 6 cm, PB = 12 cm and PC = 3 cm, what is the length of CD in cm?
- A.
21
- B.
24
- C.
6
- D.
12
Answer: Option A
Explanation :
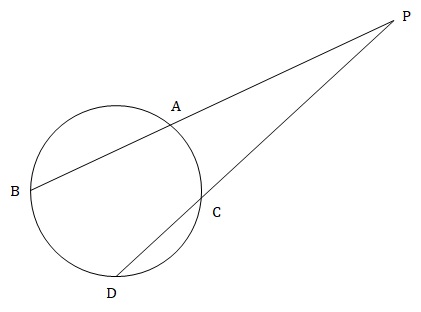
For a circle, if two chords AB and CD intersect at a single point P outside the circle, then,
PA × PB = PC × PD
∴ 6 × 12 = 3 × PD
∴ PD = 24 cm
∴ CD = PD – PC = 24 – 3 = 21 cm.
Hence, option (a).
Workspace:
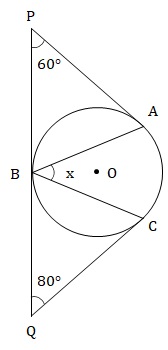
In the given figure, PBQ is a straight line while PA, PB, QB, and QC are tangents to the circle with center O. Find the value of angle AOC.
- A.
70°
- B.
80°
- C.
60°
- D.
100°
- E.
None of these
Answer: Option E
Explanation :
In ∆PAB,
PA = PB …(tangents from an external point to a circle are congruent)
∴ m ∠PBA = m ∠PAB; …(angles opposite to congruent sides)
∴ m ∠PBA = 60° …(sum of angles in a triangle is 180°)
Similarly, in ∆QBC
m ∠CBQ = m ∠BCQ = 50°
∵ m ∠PBA + m ∠CBQ + x = 180° …(linear angles)
∴ x = 180° – 60° – 50° = 70°
Now, m ∠AOC = 2 × x
∴ m ∠AOC = 140°
Hence, option (e).
Workspace:
In the figure, PA and PC are tangents to the circle ABC. If ∠P = 48°, then ∠ABC = ?

Answer: 114
Explanation :

Draw two lines joining A and C with center O.
Now in quadrilateral AOCP, sum of all four angles should be 360°.
Also, ∠OAP = ∠OCP = 90° (radius is line joining center and point of tangency is perpendicular to the tangent)
∴ 90° + ∠AOC + 90° + 48° = 360°
⇒ ∠AOC = 132°
Angle subtended by chord AC in the major segment is half of the angle it subtends at the center.
∴ ∠ADC = ½ × ∠AOC = 66°
Now, angles subtended by a chord in different segments are supplementary.
∴ ∠ADC + ∠ABC = 180°
⇒ ∠ABC = 180° - 66° = 114°.
Hence, 114.
Workspace:
In the following figure, lines AP, AQ and BC are tangent to the circle. The length of AP = 22. Find the perimeter of triangle ABC.

Answer: 44
Explanation :
We know 2 tangents drawn from an external point to a circle are equal in length.
⇒ AP = AQ = 22
∴ If we consider point B as the external point, we have two tangents i.e., BP and BD.
⇒ BP = BD
Similarly, if we consider point C as the external point, we have two tangents i.e., CD and CQ.
⇒ CD = CQ
Now, Perimeter of ∆ABC = AB + BD + CD + AC
= AB + BP + CQ + AC
= AP + AQ
= 22 + 22 = 44
Hence, 44.
Workspace:
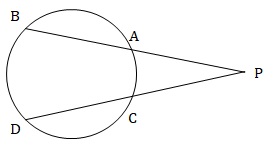
In the following figure, if PC = 6, CD = 9, PA = 5 and AB = x, find the value of x?
Answer: 13
Explanation :
When two secants are drawn from an external point to a circle
⇒ PC × PD = PA × PB
∴ 6 × 15 = 5 × (5 + AB)
⇒ AB = 13
Hence, 13.
Workspace:
In the following figure, PC = 9, PB = 12, PA = 18, and PF = 8. Then, find the length of DE.

Answer: 2.5
Explanation :
If we consider the smaller circle, two secants are drawn from P.
∴ PC × PB = PF × PE
⇒ 9 × 12 = 8 × PE
⇒ PE = 27/2
Now, if we consider the bigger circle, two secants are drawn from P.
∴ PB × PA = PE × PD
⇒ 12 × 18 = 27/2 × PD
⇒ PD = 16
∴ DE = PD – PE = 16 – 27/2 = 16 – 13.5 = 2.5
Hence, 2.5.
Workspace:
In the following figure, if PT = 6 and AB = 5, find PB?

Answer: 9
Explanation :
Let PA = x
When a secant and a tangent are drawn from an external point to a circle
⇒ PA × PB = PT2
∴ x × (x + 5) = 62
⇒ x2 + 5x – 36 = 0
⇒ (x + 9)(x - 4) = 0
∴ x = -9 or 4. (x = -9 is rejected)
∴ PB = x + 5 = 9.
Hence, 9.
Workspace:
PQ is the chord of a circle whose center is O. ROS is a line segment originating from a point R on the circle that intersect PQ produced at point S such that QS = OR. If ∠QSR = 30°, then what is the value (in degrees) of POR?
- A.
30
- B.
45
- C.
60
- D.
90
Answer: Option D
Explanation :
We can draw the following figure from the given information.
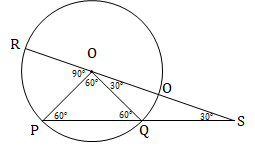
Since OR = OP = OQ = OS (radius)
⇒ ∠OPQ = ∠OQP & ∠QSO = ∠QOS
⇒ ∠POQ = 60°
⇒ ∠POR = 180 - (60° + 30°) = 90°
Hence, option (d).
Workspace:
In the figure given below (not drawn to scale), A, B and C are three points on a circle with center O. The chord BA is extended to a point T such that CT becomes a tangent to the circle at point C. If ∠ATC = 30° and ∠ACT = 50°, then ∠BOA is (in degrees)?
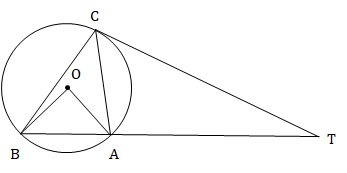
Answer: 100
Explanation :
Given, ∠ATC = 30° and ∠ACT = 50°
In ∆ACT, external angle ,
∠CAB = ∠ACT + ∠ATC = 50° + 30° = 80° …(1)
Also, chord CA and tangent CT make an angle of 50°, hence ∠CBA = 50°.
[Angle made by a chord and tangent is same as the angle subtended by the chord in opposite segment.]
Now, in ∆ABC, sum of all angles = 180°
⇒ ∠CBA + ∠BAC + ∠ACB = 180°
⇒ 50° + 30° + ∠ACB = 180°
⇒ ∠ACB = 100°
Now, angle make by a chord in major segment is half the angle it subtends at the center.
∴ ∠AOB = 2 × ∠ACB
⇒ ∠AOB 2 × 100° = 200°
Hence, 100.
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Ask Doubt
Ask Doubt Report
Report