Concept: Mixture & Alligation
Two or more items are mixed together to form a mixture. Mixture problems involve finding the average attribute (cost, concentration, percentage, etc.) of the resulting mixture. Sometimes different liquids are mixed together to get a desired concentration of the mixture. Sometimes two or more items of different costs are mixed together. The concept of simple averages can be used to solve problems when two or more items are mixed in the same quantity. The concept of weighted averages is used to solve problems when different weights of two or more items are mixed.
Mixture & Alligation is very important topic for any MBA Entrance Test. Questions on this topic involve the concept of ratio & proportion and sometimes basics of percentage also.
Mixtures are generally of two types. When two different ingredients are mixed together. It is known as simple mixture, e.g. a mixture of Water & Milk.
When two or more simple mixtures are mixed together to form another mixture, it is known as a Compound Mixture.
Kindly go through the concept of weighted average before you solve questions based on mixtures.
Example: Three lumps of gold, weighing 5g, 7g and 3g and of 15, 10 and 13 carats fineness respectively are mixed together. What is the fineness of the resultant lump?
Solution:
Here we need to calculate weighted average fineness.
Resultant fineness = =
∴ Resultant fineness = 12
Example: In two alloys, copper and zinc are related in the ratios of 4 : 1 and 1 : 3. 10 kg of alloy A, 16 kg of alloy B and some of pure copper are melted together. An alloy C was obtained in which the ratio of copper to zinc was 3 : 2. Find the weight of the new alloy.
Solution:
Let the quantity of pure copper mixed be 'x' kgs.
∴ Total copper in the final mixture = Pure copper + copper in alloy A + copper in alloy B
Copper in alloy A = 4/5 × 10 = 8 kgs
Copper in alloy B = 1/4 × 16 = 4 kgs
Total copper in final mixture = 3/5 × (10 + 16 + x)
⇒ (10 + 16 + x) = x + 8 + 4
30 + 48 + 3x = 5x + 40 + 20
∴ x = 9 kgs
Example: Three containers whose volumes are in the ratio of 2 : 3 : 4 are full of mixture of spirit and water. In the 1st container, the ratio of spirit and water is 4 : 1, in the second container 11 : 4 and in the third container 7 : 3. All the three mixtures are mixed in a bigger container. What is the ratio of spirit and water in the resulting mixture?
Solution:
Let the volumes of the three containers be 60, 90 and 120 liters respectively.
[To make calculations easier we take LCM of sum of three proportions i.e. LCM(5, 15, 10) = 30. Now
we assume the three quanties to be 2 × 30, 3 × 30 andn 4 × 30]
Quantity of spirit in container 1 = 4/5 × 60 = 48 liters
Quantity of spirit in container 2 = 11/15 × 90 = 66 liters
Quantity of spirit in container 3 = 7/10 × 120 = 84 liters
∴ Total quantity of spirit in final mixture = 48 + 66 + 84 = 198 liters
Total quantity of the mixture = 60 + 90 + 120 = 270 liters
∴ Quantity of water in final mixture = 270 - 198 = 72
⇒ = =
Example: 125 gallons of mixture of wine and water contains 20% water. How much water must be added to it to make water 25% in the new mixture?
Solution:
If water is 20%, wine will be 80% i.e., 4/5th
Quantity of wine in the mixture = 125 × 4/5 = 100 gallons
Let x liters of water is added. Total quantity of the mixture will now become 125 + x liters
Since water should become 25%, hence wine should become 75% of the new mixture.
⇒ 100 = 75% of (125 + x)
⇒ 400 = 375 + 3x
⇒ x = 25/3 gallons.
The alligation rule states that,
When different quantities of same or different ingredients, of different cost (value) are mixed together to produce a mixture of a mean cost (value), the ratio of their quantities are inversely proportional to the differences in their cost from the mean cost (value).
Suppose two varieties of wheat, A and B are mixed together. Quantities mixed are QA and QB while their cost per kg is CA and CB. If the cost per kg of the mixture is C, then
C =
⇒ C × QA + C × QB = QA × CA + QB × CB
⇒ C × QA - QA × CA = QB × CB - C × QB
⇒ QA(C - CA) = QB(CB - C)
⇒ =
This can easily be applied using the following diagram
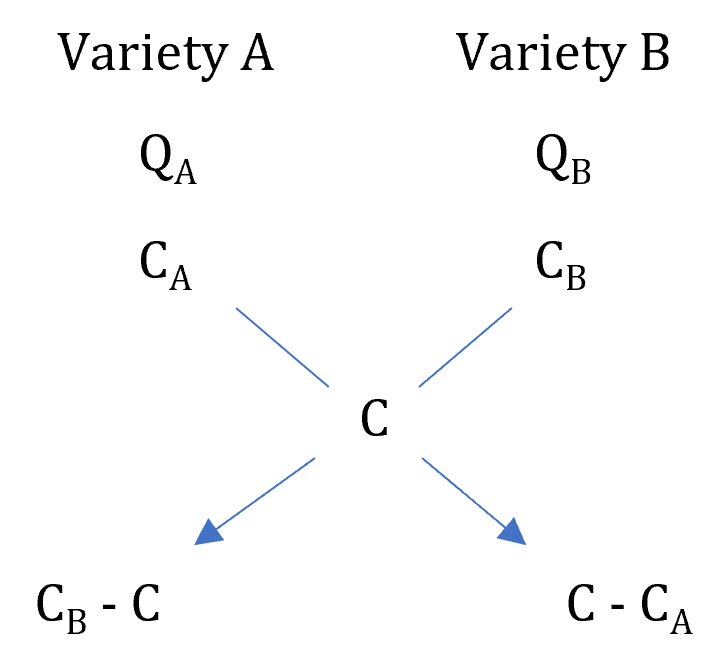
As discussed in the weighted average topic, C should always lie between CA and CB
Note: While calculating the difference, subtract the smaller quantity from the bigger one.
Example: In what proportion must rice at Rs. 3.10 per kg be mixed with rice at Rs. 3.60 per kg, so that the mixture be worth Rs. 3.25 a kg?
Solution:
Here, CA = 3.1/kg, CB = 3.6/kg and C = 3.25/kg
The best way to apply alligation rule is using the diagram approach.
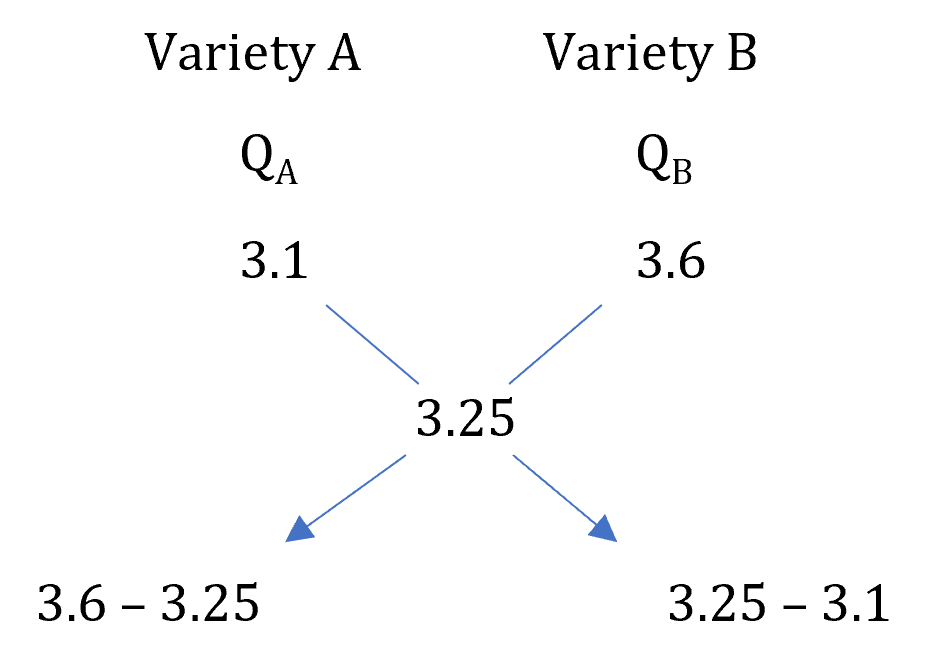
∴ = = =
∴ They must be mixed in the ratio 7 : 3
Example: A mixture of certain quantity of milk with 16 litres of water is worth 90 P per litre. If pure milk be worth Rs. 1.08 per litre how much milk is there in the mixture?
Solution:
Price of pure milk = 108 paise / liter
Price of water = 0
Price of the mixture = 90 paise / liter
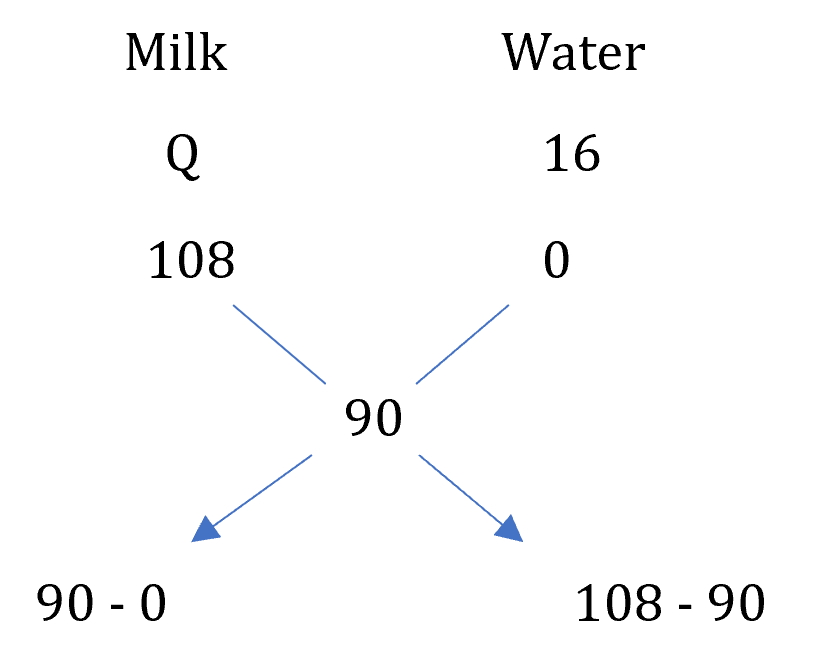
∴ =
⇒ =
∴ Quantity of milk in the mixture = 5 × 16 = 80 litres.
Example: A man lends a sum of Rs. 1200 for 3 years. A part of it he lends at 4% and the rest at 6% and receives Rs. 192 as interest after three years on the whole. How much money does he lend at each rate of interest?
Solution:
Overall rate of interest on Rs. 1200 = × 100 =
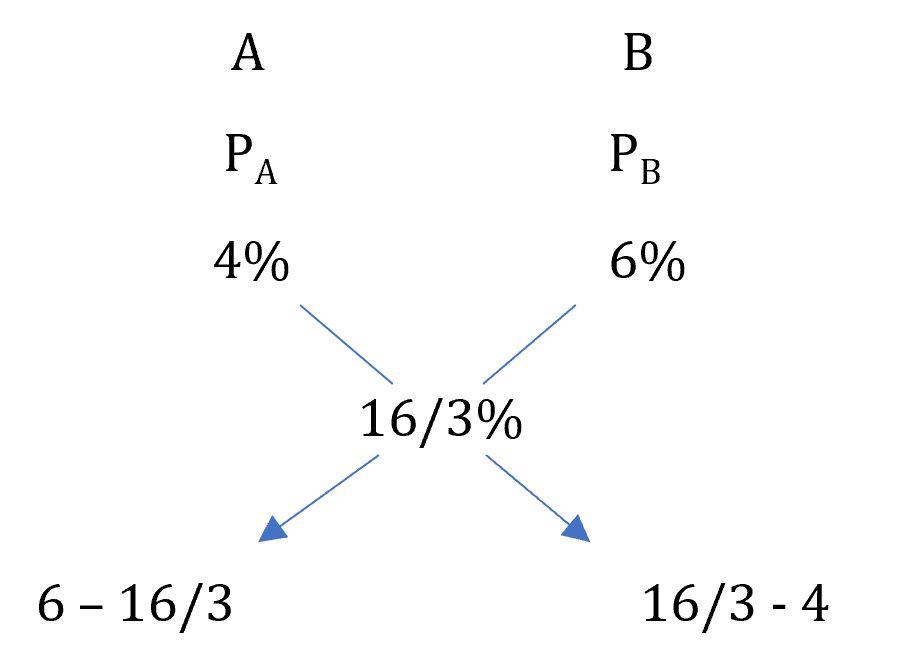
∴ = = =
∴ Money lent at 4% = 1/3 × 1200 = Rs. 400
and Money lent at 6% = 2/3 × 1200 = Rs. 800
Example: A man buys a cow and a buffalo for Rs. 10,000. He sells the cow at a profit of 10% and the buffalo at a profit of 20%. If his overall profit is 17.5%, find the cost price of each.
Solution:
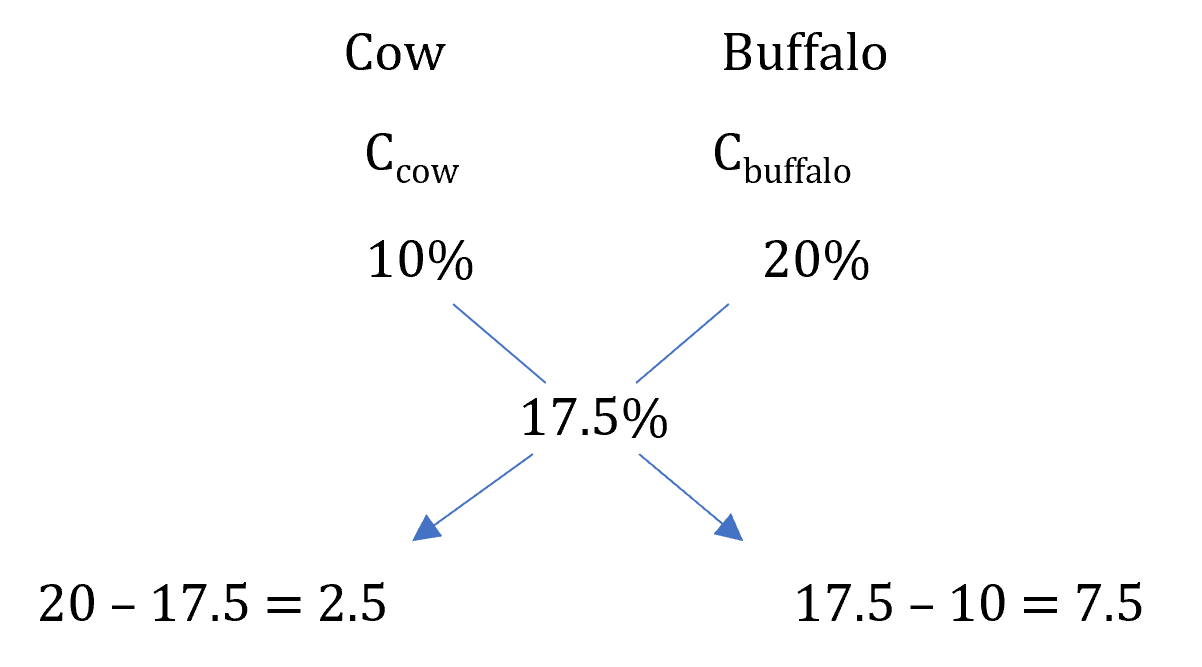
∴ = =
⇒ Cost of Buffalo = 3/4 × 10,000 = Rs. 7,500
Example: A table and a cupboard cost Rs. 3500. Table is sold at a gain of 20% and the cupboard at a loss of 10%. If gain on the outlay be Rs. 400 find the cost price of the cupboard.
Solution:
Total profit % = 400/3500 × 100 = 80/7%
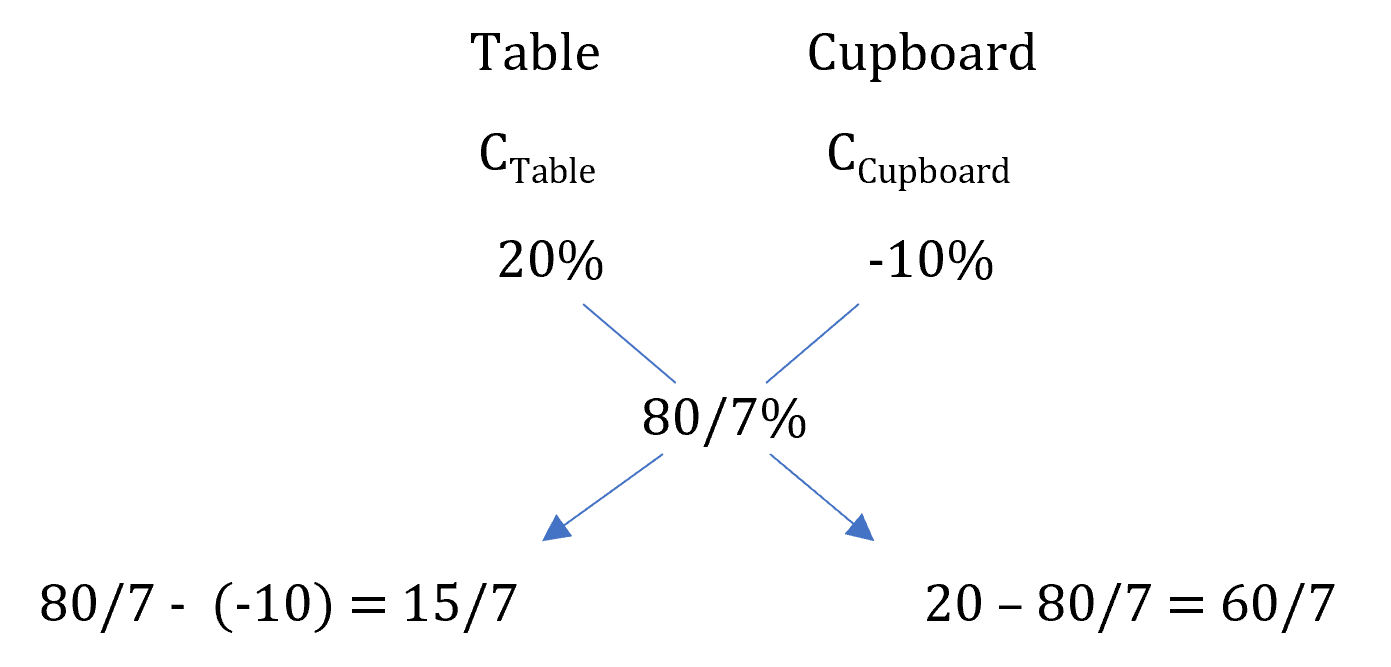
∴ = =
⇒ Cost of Cupboard = 2/7 × 3,500 = Rs. 1,000
Example: A butler stole wine from a butt of sherry which contained 40% of spirit. He replaced what he had stolen by wine containing only 16% spirit; the butt was then of 24% strength only. How much of the butt did he steal?
Solution:
Let the amount of wine stolen be x liters out of 100 liters.
Now, (100 - x) liters of 40% spirit is mixed with x liters of 16% spirit to get a 24% spirit solution.
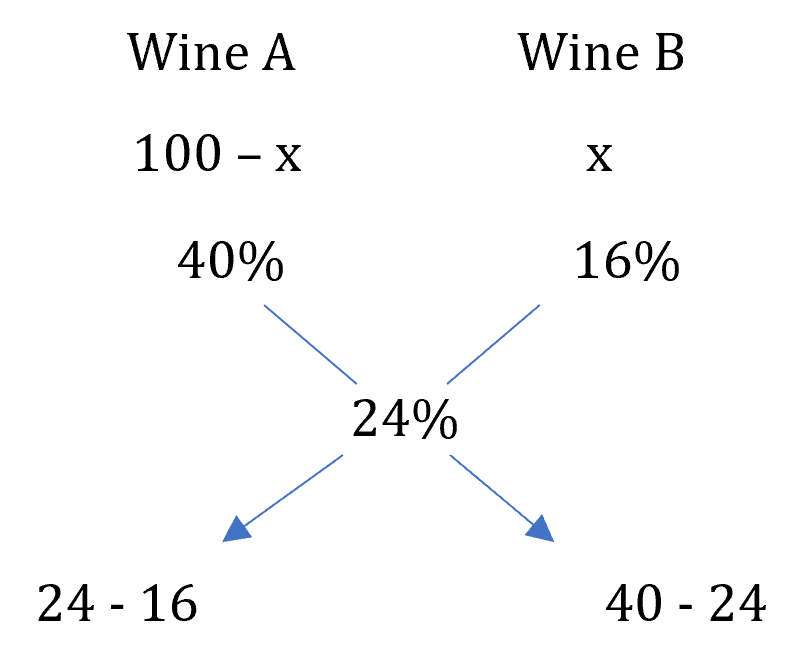
∴ = =
⇒ 200 - 2x = x
⇒ x = 200/3 liters
∴ fraction of wine stolen = = rd
Example: Two mixtures containing milk and water in the ratio 1 : 2 and 2 : 1 are mixed to get a final mixture which contains milk and water in the ratio 3 : 5. Find the ratio of quantities of two mixtures.
Solution:
Let the quantities of two mixtures be 'a' and 'b' respectively.
Fraction of milk in first mixture = 1/3
Fraction of milk in second mixture = 2/3
Fraction of milk in final mixture = 3/5
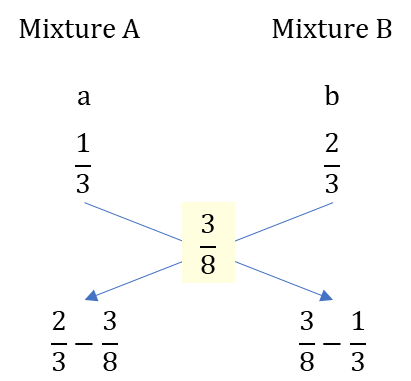
∴ = =
∴ The two mixtures are mixed in the ratio of 1 : 4.
Let us understand the concept of removal and replacement with an example.
Example: From 20 liters of a milk solution, 4 liters is taken out and then replaced with water. From the resultant mixture, again 4 liters is taken out and replaced with water. What is the quantity of milk in the final solution?
Solution:
1st Replacement:
4 liters is taken out from 20 liter solution.
∴ fraction of solution removed = = th
∴ fraction of milk removed = th
∴ fraction of milk remaining = 1 - = th
Since only water is added.
⇒ Quantity of milk remaining after 1st replacement = 4/5 × 20 = 16 liters.
2nd Replacement
Now, again 1/5th of the solution is taken out, hence 1/5th of milk will be taken out.
∴ Quantity of milk remaining after 2nd replacement = 4/5 × 16 = 12.8 liters.
From a 'V' liter solution of A, if r liters is removed and replaced with B.
Fraction of solution removed =
∴ Fraction of A removed =
∴ Fraction of A remaining = 1 -
∴ Quantity of A remaining = V
If this process is repeated a total of 'n' times.
∴ Quantity of A remaining = V
In general, from a solution containing A and B, r liters is removed and replaced with B. If this process is repeated a total of 'n' times, then
Final Quantity of A remaining = Initial Quantity of A ×
Note: This formula will be application for component which is getting diluted. Here A is getting diluted. We will not be able to get the final quantity of B using this formula.
Example: A milkman mixes 10 liters of water in 40 liters of milk. After selling one-fourth of this mixture, he addes water to replenish the quantity that he had sold. What is the current ratio of water to milk?
Solution:
Since milk is getting diluted let us calculate the quantity of milk in final solution.
Total quantity initially = 10 + 40 = 50 liters
Quantity of milk initially = 40 liters
1/4th of the solutions has been sold, i.e. one-fourth of milk has been removed.
∴ Quantity of milk remaining = 3/4 × 40 = 30 liters
Final quantity of the solution = 50 - 12.5 + 12.5 = 50 liters.
∴ Final quantity of water = 50 - milk = 50 - 30 = 20 liters.
Ratio of water to milk = 20 : 30 = 2 : 3
Example: 9 litres out of 90 litres milk are replaced with an equal quantity of water. Again 9 litres of the resultant milk water solution are replaced with an equal quantity of water. Find the final concentration of milk in the solution after the second iteration.
Solution:
Since milk is getting diluted let us calculate the quantity of milk in final solution.
Final Quantity of milk remaining = Initial Quantity of milk ×
⇒ Final Quantity of milk remaining = 90 ×
⇒ Final Quantity of milk remaining = 90 ×
⇒ Final Quantity of milk remaining = 90 × = 90 ×
∴ Final concentraction of milk = × 100 = 81%
Example: A vessel is completely filled with petrol. 10 litres is drawn from this vessel and replaced with kerosene. 10 litres of the petrol kerosene mixture is again drawn from the vessel and replaced with kerosene. After the second iteration, the ratio of petrol and kerosene in the vessel is 49 : 32. Find the capacity of the vessel.
Solution:
Let the capacity of the vessel be 'V' liters.
Final Quantity of milk petrol = × V
⇒ Final Quantity of petrol = Initial Quantity of petrol ×
⇒ × V = V ×
⇒ =
⇒ =
⇒ =
⇒ = =
∴ V = 45 liters