Concept: Geometry Basics

 

Point: It is an exact location. It is a fine dot which has neither length nor breadth nor thickness but has position i.e. it has no magnitude.

Line: A line is a set of all the points in one dimension. It can be extended in both the directions; hence, its length is infinite. A line does not have either width or thickness.

Intersecting lines: Two lines having a common point are called intersecting lines. The common point is known as the point of intersection.

Line Segment: The straight path joining two points A and B is called a line segment AB. It has end points and a definite length.

Ray: A line segment which can be extended in only one direction is called a ray.

Concurrent lines: If two or more lines intersect at the same point, then they are known as concurrent lines.

Plane: A plane is set of all the points in two dimensions. It does not have any thickness but is indefinitely extended in all directions.

​​​​​​​

Angles: when two straight lines meet at a point they form an angle.

​​​​​​​

In the figure above, the angle is represented as ∠AOB. OA and OB are the arms of ∠AOB. Point O is the vertex of ∠AOB. The amount of turning from one arm (OA) to other (OB) is called the measure of the angle (AOB).

Right angle: An angle whose measure is 90° is called a right angle.

​​​​​​​

Acute angle: An angle whose measure is less than one right angle (i.e. less than 90°), is called an acute angle.

​​​​​​​

Obtuse angle: An angle whose measure is more than one right angle and less than two right angles (i.e. less than 180° and more than 90°) is called an obtuse angle.

​​​​​​​

Straight angle: An angle that measure exactly 180° is called a straight angle. The angle shown in the figure below is a straight angle.

​​​​​​​

Reflex angles: An angle whose measure is more than 180° and less than 360° is called a reflex angle.

​​​​​​​

Complementary angles: If the sum of the two angles is one right angle (i.e. 90°), they are called complementary angles. Therefore, the complement of an angle θ is equal to 90° - θ.

​​​​​​​

Supplementary angles: Two angles are said to be supplementary, if the sum of their measures is 180°. Therefore, supplement of an angle θ is 180° - θ.

​​​​​​​

Bisector of an angle: If a ray or a straight line passing through the vertex of that angle, divides the angle into two angles of equal measurement, then that line is known as the bisector of that angle.

​​​​​​​

A point on an angle bisector is equidistant from both the arms.

​​​​​​​

In the figure above, Q and R are the feet of perpendiculars drawn from P to OB and OA. It follows that PQ = PR.

Vertically opposite angles: When two straight lines intersect each other at a point, the pairs of opposite angles so formed are called vertically opposite angles.

In the above figure, ∠1 and ∠3, ∠2 and ∠4 are vertically oppostie angles.

Vertically opposite angles are always equal.

​​​​​​​

Adjacent angle: When two angles share a common side and a common vertex, we get two adjacent angles. For two angles to be adjacent, no angles should be inside the other.

​​​​​​​

If the sum of two adjacent angles is 180° then these angles form a linear pair.

Angles making a linear pair are supplementary to each other.

Perpendicular lines: Two lines intersecting each other at 90° are said to be perpendicular to each other.

​​​​​​​

Parallel lines: Two lines are parallel if they are coplanar and they do not intersect each other even if they are extended on either side.

​​​​​​​

Two lines in the same plane that are perpendicular to a given line are parallel to each other.

​​​​​​​

Line segment bisector: A line segment bisector which makes an angle of 90° with the given segment is known as the perpendicular bisector for the given segment.

​​​​​​​

Any point of the perpendicular bisector is at an equal distance from both the ends of the given line segment.

​​​​​​​

Here, PA = PB

Distance of a point from a line means the length of the perpendicular drawn from the point to the line. It is the shortest distance of the point from the line.

​​​​​​​

Distance between L₁ and point P is PX.

Distance between two parallel lines is the perpendicular distance between them.

​​​​​​​

Distance between L₁ and L₂ is XY.

Distance between two coplanar but non-parallel lines is always zero, because these lines intersect each other at some point.

Transversal: A transversal is a line that intersects (or cuts) two or more coplanar lines at distinct points.

​​​​​​​

In the above, figure, a transversal t is intersecting two parallel lines, l and m, at A and B, respectively.

Angles formed by a transversal of two parallel lines:

​​​​​​​

In the above figure, L₁ and L₂ are two parallel lines intersected by a transversal. The following properties of the angles can be observed: 

• Vertically opposite angles are equal: a = d, b = c, e = h and f = g
• Alternate interior angles are equal: c = f and d = e
• Alternate exterior angles are equal: a = h and b = g
• Corresponding angles are equal: a = e, b = f, c = g and d = h
• Interior angles on the same side of the transversal are supplementary: c + e = 180° and d + 180°
• Exterior angles on the same side of the transversal are supplementary: a + g = 180° and b + h = 180°

 

​​​​​​​

For a set of three or more parallel lines (L₁, L₂ and L₃ for example), and two transversals (T₁ and T₂ for example), the ratio of the lengths of the intercepts of any transversal is equal 

i.e., $\frac{\mathrm{AB}}{\mathrm{BC}}$ = $\frac{\mathrm{PQ}}{\mathrm{QR}}$

 

Triangles are closed figures containing three angles and three sides.

​​​​​​​

Altitude: Line joining a vertex and perpendicular to the opposite side.
Median: Line joining a vertex and mid-point of the opposite side.
Angle Bisector: Line drawn from a vertex which bisects the given internal angle.

AD here is the altitude from vertex A. AE is the median.

 

Acute Triangle

​​​​​​​

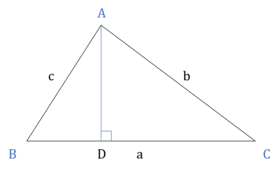
• All angles are < 90°

• All general properties of ∆s apply.




• Check for an Acute triangle.

  In a ∆, if c is the longest side and c² < a² + b², then it is an Acute triangle.

Right Triangle

​​​​​​​

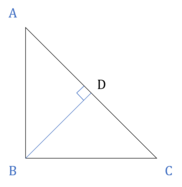
• Exactly one angle is 90°.

• All general properties of ∆s apply.

• Hypotenuse² = Base² + Perpendicular²

• Area = $\frac{1}{2}$ × AB × BC




• Altitude BD = $\frac{\mathrm{(AB\; \times \; BC)}}{\mathrm{AC}}$

• Altitude BD = $\sqrt{\mathrm{AD}\times \mathrm{CD}}$

• Midpoint of the hypotenuse is equidistant from the three vertices i.e. EA = EB = EC. It implies that the circumradius of a right-angled triangle is half of the hypotenuse.

  ⇒ R = $\frac{\mathrm{Hypotenuese\; (c)}}{2}$

• Inradius = $\frac{\mathrm{(a\; +\; b\; -\; c)}}{2}$




• Check for a Right triangle.

  In a ∆, if c is the longest side and c² = a² + b², then it is a Right triangle.

Obtuse Triangle

​​​​​​​

• Exactly one angle is > 90°.

• All general properties of ∆s apply.




• Check for an Obtuse triangle.

  In a ∆, if c is the longest side and c² > a² + b², then it is an Obtuse triangle.

Scalene Triangle

• No 2 sides are equal.

• No 2 angles are equal.

• All the general properties of a triangle apply.

Isosceles Triangle

​​​​​​​

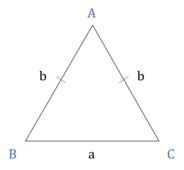
• Exactly 2 sides are equal.

• The angles opposite to the equal sides are also equal.

• All the general properties of a triangle apply.

• Altitude from the vertex containing equal sides is the Median as well the Angle Bisector (i.e. it divides the in ∆ two equal halves).

• In an isosceles triangle, all the four points, viz, circumcenter, incenter, centroid and orthocenter lie on the median drawn from the vertex contained by equal sides to the non-equal side.

Equilateral Triangle

​​​​​​​

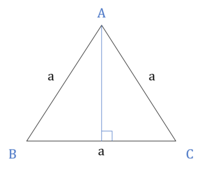
• All sides are equal (a).

• All angles are equal to 60°.

• All the general properties of a triangle apply.

• Height of the triangle = $\frac{\sqrt{3}}{2}$a

• Area of the triangle = $\frac{\sqrt{3}}{4}$a²




• Inradius = $\frac{a}{2\sqrt{3}}$

• Circumradius = $\frac{a}{\sqrt{3}}$

• Altitudes, Medians, Angle Bisectors are all same.

• In an equilateral triangle all the four points viz, circumcenter, incenter, centroid and orthocenter coincide.




• Equilateral triangle has the maximum area, out of all the triangles that can be inscribed in a given circle.

30° – 60° – 90° triangle

​​​​​​​

• Side opposite to 30° = half of hypotenuse.

• Side opposite to 60° = $\frac{\sqrt{3}}{2}$ × hypotenuse

45° – 45° – 90° triangle

​​​​​​​

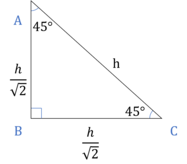
• Each of the smaller sides = $\frac{1}{\sqrt{2}}$ × hypotenuse.

• Hypotenuese = √2 × side

 

​​​​​​​

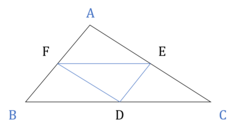
• The line joining the mid-points of any two sides of a triangle is parallel to the third side and half of it.

  ⇒ FE ∥ BC, DE ∥ AB, DF ∥ AC
  ⇒ FE = BC/2, DE = AB/2, FD = AC/2

• If we join the midpoints of three sides of a triangle, we get 4 triangles of equal areas.

  i.e., area ∆DEF = area ∆AFE = area ∆BDF = area ∆DEC = ¼ (area ∆ABC)

Corollary: If a line parallel to the base and passes through the midpoint of one side, it will pass through the midpoint of the other side also.

In a triangle if AD is the anlge bisector of ∠A meeting BC at D, then

$\frac{\mathrm{AB}}{\mathrm{AC}}$ = $\frac{\mathrm{BD}}{\mathrm{CD}}$

 

A line drawn parallel to one of the three sides of a triangle divides the other 2 sides in same proportion.

​​​​​​​

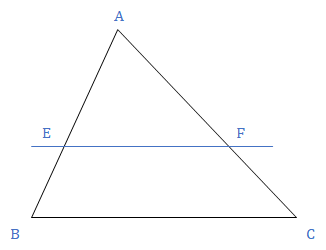
Conversely, If E and F are two points dividing AB and AC in same proportion, then EF will be parallel to BC.

Here, triangle AEF is similar to triangle ABC.

Line joining the mid-points of two sides is parallel to third side.