CRE 5 - Trigonometry | Geometry, Mensuration & Trigonometry
There are two, men and a tower in between. The distance between the men is 100 m. The angle of elevation to the top of the tower are 30° and 60° respectively. Find the height of tower.
- A.
25
- B.
25√3
- C.
25/√3
- D.
None of these
Answer: Option B
Explanation :
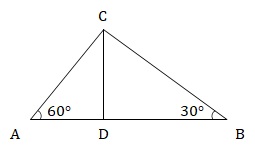
Given, AB = 100. Let AD = x, hence, BD = 100 – x.
In ∆ACD, tan60° = √3 =CD/AD
⇒ CD = √3 × AD …(1)
In ∆BCD, tan30° = 1/√3 = CD/BD.
⇒ CD = BD/√3 …(2)
From (1) and (2)
⇒ √3 × AD = BD/√3
⇒ 3x = 100 – x
⇒ x = 25.
∴ CD = √3 × AD = 25√3.
Hence, option (b).
Workspace:
A man is standing at some distance from a building. There is a pole at the top of the building. The building subtends an angle of 30° at the man and the angle of elevation of the top of the pole is 45°. Find the height of the pole if the building is 50m high.
- A.
50(√3 - 1)
- B.
50√3
- C.
50/√3
- D.
None of these
Answer: Option A
Explanation :
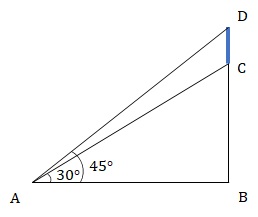
Given, BC = 50 m.
Let CD = x.
In ∆ ABC, tan45° = 1/√3 = BC/AB
⇒ AB = BC × √3 = 50√3.
In ∆ ABD, tan45° = 1 = BD/AB
⇒ BD = AB
⇒ 50 + x = 50√3
⇒ x = 50(√3 - 1)
Hence, option (a).
Workspace:
A plane flies above a man at a height of 1000m. The angle of elevation changes from 60° to 30° in 5 sec. Find speed of plane.
- A.
400(√3 – 1) m/s
- B.
400√3 m/s
- C.
400/√3 m/s
- D.
400/(√3 + 1) m/s
Answer: Option C
Explanation :
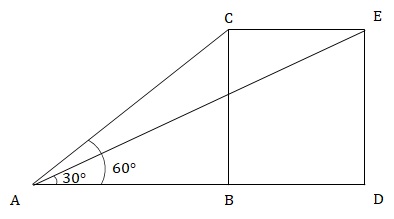
Given, BC = DE = 1000 m
In ∆ABC, tan60° = √3 = BC/AB
⇒ AB = BC/√3 = 1000/√3
In ∆ABC, tan30° = 1/√3 = DE/AD
⇒ AD = DE × √3 = 1000√3
∴ BD = AD - AB = 1000√3 – 1000/√3 = 2000/√3.
∴ Plane travels 2000/√3 meters in 5 seconds.
⇒ Speed of the plane = (2000/√3) ÷ 5 = 400/√3 m/s.
Hence, option (c).
Workspace:
A tree breaks down at some point and touches the ground with the tip making 30° angle with the ground. If the tree is 30 m long; find how high from the ground it broke (in meters).
- A.
12
- B.
15
- C.
20
- D.
10
Answer: Option D
Explanation :

Let the tree broke at a height of x meters from the ground i.e., BC = x.
∴ AC = 30 – x.
In ∆ABC, sin30° = 1/2 = BC/AC
⇒ AC = 2BC
⇒ 30 – x = 2x
⇒ x = 10 meters.
Hence, option (d).
Workspace:
A ladder makes 60° with ground when it leans against the wall. The ladder slides down by 5 m along the ground making the angle 45°. Find the length of the ladder.
- A.
10√2
- B.
10/(√2 + 1)
- C.
10/(√2 - 1)
- D.
10(√2 + 1)
Answer: Option D
Explanation :
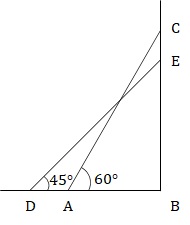
Let the length of the ladder be x, i.e., AC = DE = x.
In ∆ABC, cos60° = 1/2 = AB/AC
⇒ AB = AC/2 …(1)
In ∆DBE, cos45° = 1/√2 = DB/DE
⇒ DB = DE/√2 …(2)
We know, DB – AB = 5.
From (1) and (2)
DE/√2 – AC/2 = 5
⇒ x/√2 – x/2 = 5
⇒ (√2 - 1)x/2 = 5
⇒ x = 10/(√2 - 1) = 10(√2 + 1).
Hence, option (d).
Workspace:
Harsha is riding vertically in a hot air balloon, directly over a point A on the ground. Harsha spots a parked car on the ground at an angle of depression of 30°. The balloon rises 50 meters. Now the angle of depression to the car is 60 degrees. How far is the car from point A?
- A.
25
- B.
25√3
- C.
25/√3
- D.
None of these
Answer: Option B
Explanation :
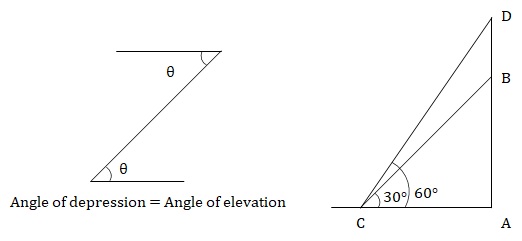
Given, BD = 50 m.
Let AC = x.
In ∆CAB, tan30° = 1/√3 = AB/AC
⇒ AB = x/√3 = x/√3 …(1)
In ∆CAD, tan60° = √3 = AD/AC
⇒ AD = √3 × x = √3 × x …(2)
We know, AD – AB = BD = 50
From (1) and (2)
⇒ √3x – x/√3 = 50
⇒ 2x/√3 = 50
⇒ x = 25√3.
Hence, option (b).
Workspace:
If the shadow of a building increases by 10 meters when the angle of elevation of the sun rays decreases from 60° to 45°, what is the height of the building?
- A.
10√3
- B.
10/(√3 - 1)
- C.
10√3/(√3 + 1)
- D.
None of these
Answer: Option B
Explanation :
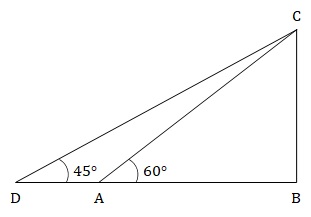
Initially the shadow of CB is AB and later the shadow becomes DB.
Let BC = x
In ∆ABC, tan60° = √3 = BC/AB
⇒ AB = x/√3
In ∆DBC, tan45° = 1 = BC/DB
⇒ DB = x
We know, DB – AB = AD = 10 meters.
⇒ x – x/√3 = 10
⇒ (√3 - 1)x/√3 = 10
⇒ x = 10√3/(√3 - 1)
Hence, option (b).
Workspace:
From the top of a 200 meters high building, the angle of depression to the bottom of a second building is 60 degrees. From the same point, the angle of elevation to the top of the second building is 45 degrees. Calculate the height of the second building.
- A.
200(√3 + 1)/√3
- B.
200(√3 + 1)
- C.
200√3
- D.
None of these
Answer: Option A
Explanation :

Given, AB = 200 meters. Let CD = x.
∴ DE = 200 and CE = x – 200.
In ∆AED, tan60° = √3 = DE/AE
⇒ AE = DE/√3 …(1)
In ∆AEC, tan45° = 1 = CE/AE
⇒ AE = CE …(2)
From (1) and (2)
DE/√3 = CE
⇒ 200/√3 = x – 200
⇒ x = 200/√3 + 200 = 200(√3 + 1)/√3
Hence, option (a).
Workspace:
A plane flies above a man at a height of 1000 m. At one time, angle of elevation is 60°. Suddenly, the plane climbs up at an angle of 30° and 5 seconds later angle of elevation becomes 45°. Speed of plane is?
- A.
200√3
- B.
2000/√3
- C.
400√3
- D.
400/√3
Answer: Option D
Explanation :
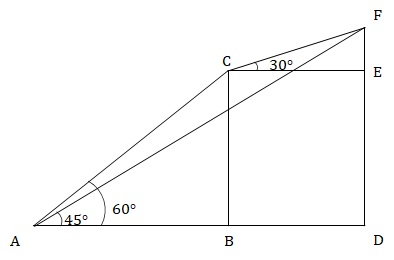
Given, height of plane initially (BC) = 1000 meters.
Let CF = x
In ∆CFE, cos30° = √3/2 = CE/CF
⇒ CE = √3x/2 = BD …(1)
Also, sin30° = 1/2 = FE/CF
⇒ FE = x/2 …(2)
In ∆ABC, tan60° = √3 = CB/AB
⇒ AB = CB/√3 = 1000/√3 …(3)
In ∆AFD, tan45° = 1 = FD/AD
⇒ AD = FD …(4)
We know, BD = AD – AB = FD – AB
⇒ BD = (DE + EF) - AB
From (1), (2) and (3)
√3x/2 = (1000 + x/2) – 1000/√3
Solving this we get x = 2000/√3
∴ Plane travels 2000/√3 meters in 5 seconds.
⇒ Speed of the plane = (2000/√3) ÷ 5 = 400/√3.
Hence, option (d).
Workspace:
A man looks up at a pole making angle of elevation is 45°. When he looks at the reflection of the tip of the pole in water, he finds the angle of depression as 60°. If the man is 1 m tall, find height of the pole.
- A.
1/(3 - 2√3)
- B.
2 - √3
- C.
2 + √3
- D.
None of these
Answer: Option C
Explanation :

EA is the line representing the ground.
Height of the man (represented by AB) = 1 meter.
Let height of the pole (ED) = x meters.
In ∆BFD, tan45° = 1 = DF/BF
⇒ BF = DF …(1)
In ∆BFD, tan60° = √3 = CF/BF
⇒ BF = CF/√3 …(2)
From (1) and (2)
DF = CF/√3
⇒ x – 1 = (x + 1)/√3
⇒ √3x - √3 = x + 1
⇒ √3x - x = 1 + √3
⇒ x = (√3 + 1)/(√3 - 1)
⇒ x = (√3 + 1)2/2
⇒ x = (4 + 2√3)/2 = 2 + √3
Hence, option (c).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Ask Doubt
Ask Doubt Report
Report