IPMAT (I) 2022 QA MCQ | Previous Year IPMAT - Indore Paper

Answer: Option A

Explanation :

Given, ${\log }_{27}\left(8\right)$ ≤ ${\log }_3\left(x\right)$ < $9^{\frac{1}{{\log }_2\left(3\right)}}$ 

⇒ ${\log }_{3^3}\left(2^3\right)$ ≤ ${\log }_3\left(x\right)$ < $9^{{\log }_3\left(2\right)}$ 

⇒ $\frac{3}{3}{\log }_3\left(2\right)$ ≤ ${\log }_3\left(x\right)$ < $2^{{\log }_3\left(9\right)}$ 

⇒ ${\log }_3\left(2\right)$ ≤ ${\log }_3\left(x\right)$ < $2^2$ 

⇒ ${\log }_3\left(2\right)$ ≤ ${\log }_3\left(x\right)$ < 4

⇒ ${\log }_3\left(2\right)$ ≤ ${\log }_3\left(x\right)$ < ${\log }_3\left(3^4\right)$

⇒ 2 ≤ x < 81

∴ x ∈ [2, 81)

Hence, option (a).

Answer: Option C

Explanation :

(81)^x + (81)^f(x) = 3 

⇒ (3)^4x + (3)^4f(x) = 3 

⇒ (3)^4x-1 + (3)^4f(x)-1 = 1   ...(1)

Now, power of a positive number is always greater than 0.

∴ (3)^4x-1 > 0 and (3)^4f(x)-1 > 0

From (1): Sum of two positive numbers is 1. This is only possible when both number are less than 1.

⇒ (3)^4f(x)-1 < 1

⇒ 4f(x) - 1 < 0

⇒ f(x) < 1/4 or 0.25

∴ f(x) ∈ (-∞, 0.25)

Hence, option (c).

Answer: Option C

Explanation :

Three lines are cocurrent when they meet at a single point i.e., the equations representing these lines have a common solution.

Consider,
x − y − 1 = 0 ...(1) and
2x + 3y − 12 = 0   ...(2)

(2) + 3 × (1) 
⇒ 5x -15 = 0
⇒ x = 3

Putting x = 3 in (1) we get y = 2
∴ (x, y) = (3, 2) is the common solution for first two lines.

Hence, (3, 2) should also satisfy the 3rd equation.

⇒ 2 × 3 − 3 × 2 + k = 0
⇒ k = 0

Hence, option (c).

Answer: Option B

Explanation :

The three sides are x, 21 and 40.

In a triangle:
difference of other two sides < any side < sum of other two sides.

⇒ 40 - 21 < x < 40 + 21

⇒ 19 < x < 61

Only option (b) satisfies this condition.

Hence, option (b).

Answer: Option A

Explanation :

In a triangle, the line joining the mid-points of two sides is parallel to the third side and half of it.

D and E are midpoints of AB and AC respectively. Hence, DE will be parallel to BC and half of BC.

⇒ DE = BC/2

⇒ BC = 12.

Hence, option (a).

Answer: Option A

Explanation :

For a number to be divisible by 6, the sum of its digits should be divisible by 3 and it's units digit should be even.

Since, abcde is divisible by 6,
a + b + c + d + e = multiple of 3, and
e is an even number

Option (a): edcba
Here the units digit is a which is not necessarily even, hence edcba is not definitely divisible by 6.

Option (b): eee
Here units digit e is even and sum of the digits = 3e which is a multiple of 3, hence eee is definitely divisible by 6.

Option (c): bbadcacede
Here units digit ​​​​​​​e is even and sum of the digits = 2(a + b + c + d + e) which is a multiple of 3, hence eee is definitely divisible by 6.

Option (d): cdbae
Here units digit ​​​​​​​e is even and sum of the digits = (a + b + c + d + e) which is a multiple of 3, hence eee is definitely divisible by 6.

Hence, option (a).

Answer: Option C

Explanation :

Vowels: A, A, E, E
Consonants = M, N, G, M, N, T

We first arrange the consonants in $\frac{6!}{2!\times 2!}$ = 180 ways.

This can be represented as: C C C C C C

Now we have 6 places for 4 vowels:  | C | C | C | C | C | C |

Out of 7 places we can select 4 places for vowels in 7C4 = 35 ways

4 vowels can be arranged in these 4 places in $\frac{4!}{2!\times 2!}$ = 6 ways.

∴ Total number of ways of arranging = 180 × 35 × 8 = 37,800

Hence, option (c).

Answer: Option A

Explanation :

Average height of n persons initially = 160
∴ Sum of the heights of these n persons = 160n

Sum of the heighs of m persons joining = 172m

Total height of (n + m) persons = 160n + 172m

⇒ Average = 164 = $\frac{160\mathrm{n}+172\mathrm{m}}{\mathrm{n}+\mathrm{m}}$

⇒ 164n + 164m = 160n + 172m

⇒ 4n = 8m

⇒ m : n = 1 : 2

Hence, option (a).

Answer: Option B

Explanation :

The sum of the first 15 terms in an arithmetic progression is 200 , while the sum of the next 15 terms is 350 . Then the common difference is

Sum of n terms of an AP = n/2 × [2a + (n - 1)d]

Sum of first 15 terms = 200
∴ 200 = 15/2 × (2a + 14d)
⇒ 2a + 14d = 80/3   ...(1)

Sum of first 30 terms = 200 + 350 = 550
∴ 550 = 30/2 × (2a + 29d)
⇒ 2a + 29d = 110/3   ...(2)

(2) - (1), we get
15d = 30/3
⇒ d = 10/15 = 2/3

Hence, option (b).

Answer: Option C

Explanation :

A = $\left[\begin{array}{ccc}a& b& c\\ b& c& a\\ c& a& b\end{array}\right]$.

Determinant of A = a(cb - a²) + b(ac - b²) + c(ba - c²)

= 3abc - a³ - b³ - c³

= - (a³ + b³ + c³ - 3abc)

= - (a + b + c)(a² + b² + c² - ab - bc - ca)

(a + b + c)(a² + b² + c² - ab - bc - ca) > 0 for a, b, c > 0

∴ Determinant of A = - (a + b + c)(a² + b² + c² - ab - bc - ca) is always negative.

Hence, option (c).

Answer: Option B

Explanation :

Answer: Option B

Explanation :

0 < θ < π/4, let's take θ = 30°

sin30° = 1/2 = 0.5, cos30° = √3/2 = 0.866

a = ((sinθ)^sinθ)(log₂cosθ), 
⇒ a = ((1/2)^1/2)(log₂0.866) 

b = ((cosθ)^sinθ)(log₂sinθ), 
⇒ b = ((0.866)^1/2)(log₂1/2), 

c = ((sinθ)^cosθ)(log₂cosθ) 
⇒ c = ((1/2)^0.866)(log₂0.866) 

d = ((sinθ)^sinθ)(log₂sinθ)
⇒ d = ((1/2)^1/2)(log₂1/2)

(1/2)^0.5 > (1/2)^0.866 ​​​​​​​and (log₂0.866) is negative
∴ c is greater than a.

Similarly, c > a > d > b.

∴ Median of these four numbers = average of 2 middle numbers = (a + d)/2

Hence, option (b).

Answer: Option A

Explanation :

For two sets A and B with m and n elements respectively.
Total relations = 2^{m × n} 
Total functions from A to B = n^m 

Here, A = {1, 2, 3} i.e., 3 elements and B = {a, b} i.e., 2 elements.

∴ Total relations = 2^{3 × 2} = 64
Total functions from A to B = 2³ = 8

⇒ Required probability = 8/68 = 1/8.

Hence, option (a).

Answer: Option A

Explanation :

In a 400-metre race, Ashok beats Bipin and Chandan respectively by 15 seconds and 25 seconds. If Ashok beats Bipin by 150 metres, by how many metres does Bipin beat Chandan in the race?

Ashok beat Bipin by 150 metres or 15 seconds.
∴ Speed of Bipin = 150/15 = 10 m/s

Bipin takes = 400/10 = 40 seconds to complete the race.
Time taken by Ashok to complete the race = 40 - 15 = 25 seconds
Time taken by Chandan to complete the race = 25 + 25 = 50 seconds

Distance travelled by Chandan in 40 seconds = 400/50 × 40 = 320 metres.

∴ By the time (40 secs) Bipin completes the race, Chandan has completed 320 m and hence Bipin beats Chandan by 80 meters.

Hence, option (a).

Answer: Option D

Explanation :

Fruit Punch contains 60 ml orange juice, 40 ml of water and 100 ml of apple juice i.e., a total of 200 ml.

Madhu drinks 50ml i.e., 1/4^th of the this mixture, hence 3/4^th of the mixture is left..
Total solutio left = 150 ml
Orange left = 60 × 3/4 = 45 ml
Water left = 40 × 3/4 = 30 ml
Apple left = 100 × 3/4 = 75 ml

Now let x ml of orange is added to bring orange to 50% i.e., 1/2.
∴ 45 + x = 1/2 × (150 + x)​​
⇒ 90 + 2x = 150 + x
⇒ x = 60 ml

Hence, option (d).

Answer: Option A

Explanation :

Equation $\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}+\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$ represents an ellipse.

Hence, the given curve is an ellipse. We need to figure out the foci of this ellipse.

Also, Cos√2 - cos√3 > Sin√2 - Sin√3 > 0

⇒ b² > a²

∴ Foci is on y-axis.

Hence, option (a).

Answer: Option B

Explanation :

Given, f(x) = $\frac{\mathrm{x}}{\left|\mathrm{x}\right|}$

Case 1: x > 0
⇒ |x| = x
∴ f(x) = $\frac{\mathrm{x}}{\mathrm{x}}$ = 1

Case 2: x < 0
⇒ |x| = - x
∴ f(x) = $\frac{\mathrm{x}}{-\mathrm{x}}$ = - 1

∴ f(x) = 1 when x > 0 while f(x) = -1 when x < 0.

⇒ f(x) can take only two values {1, -1}.

Hence, option (b).

Answer: Option A

Explanation :

Let the two numbers be hx and hy, where h is the HCF of thest two numbers and LCM of these numbers = hxy.

Now, (hx + hy)² - (hx - hy)²
= (hx)² + (hy)² + 2h²xy - ((hx)² + (hy)² - 2h²xy)
= 4h²xy
= 4 × h × hxy
= 4 × HCF × LCM

Hence, option (a).

Answer: Option C

Explanation :

Given, price ∝ (weight)²

∴ $\frac{p_1}{p_2}$ = $\frac{{w_1}^2}{{w_2}^2}$

⇒ $\frac{3600}{p_2}$ = $\frac{{10}^2}{4^2}$ = $\frac{25}{4}$

⇒ p₂ = 3600 × 4/25 = 576

Hence, option (c).

Answer: Option C

Explanation :

Given, x² + |x + 4| + |x − 4| − 35 = 0

Here the critical points are -4 and 4.

Case 1: x ≥ 4
∴ x² + (x + 4) + (x − 4) − 35 = 0
⇒ x² + 2x - 35 = 0 
⇒ (x + 7)(x - 5) = 0
⇒ x = - 7 or 5
Since x  ≥ 4, hence x = -7 is rejected.
∴ x = 5

Case 2: - 4 ≤ x < 4
∴ x² + (x + 4) - (x − 4) − 35 = 0
⇒ x² - 17 = 0 
⇒ x² = 17 
⇒ x = ±√17
Both these values are rejected since -4 ≤ x < 4.

Case 3: x < - 4
∴ x² - (x + 4) - (x − 4) − 35 = 0
⇒ x² - 2x - 35 = 0 
⇒ (x - 7)(x + 5) = 0
⇒ x = -5 [Since x < -4]

∴ Possible solutions are 5 and -5

∴ Sum of squares of solutions = 25 + 25 = 50.

Hence, option (c).

Answer: Option D

Explanation :

2 elements of A × B are (1,4) and (4,1).

∴ 1 and 4 are elements of A and 4 and 1 are elements of B.
⇒ Both A and B have at least 2 elements.

Now, A × B has 4 elements and both A and B have at least 2 elements. This is possbile when both A and B have exactly 2 elements each.

⇒ A = {1, 4} and B = {4, 1}

⇒ A × B = {(1, 4), (1, 1), (4, 4), (4, 1)}

Also, B × A = {(4, 1), (4, 4), (1, 1), (1, 4)}

We can see that A × B = B × A.

Hence, option (d).

Answer: Option B

Explanation :

If f(x² + f(y)) = xf(x) + y for all non-negative integers x and y, then the value of [f(0)]² + f(0) equals _________.

Given, f(x² + f(y)) = xf(x) + y

Subsituting x = 1 and y = 0, we get

f(1 + f(0)) = f(1)

Now, if f(x) = f(y) it implies that x = y

Hence, 1 + f(0) = 1

⇒ f(0) = 0

∴ [f(0)]² + f(0) = [0]² + 0 = 0

Hence, option (b).

Answer: Option A

Explanation :

Number of factors of 3⁷2⁸17³ = (7 + 1)(8 + 1)(3 + 1) = 8 × 9 × 4 = 288

Number of factors of 3⁷2⁸17³ which are perfect squares = (4)(5)(2) = 40

Required probability = 40/288 = 10/72 = 5/36.

Hence, option (a).

Answer: Option C

Explanation :

Required numbers
= Numbers which are divisible by both 2 and 3 - Numbers which are divisible by both 2, 3 and 5
= Numbers which are divisible by 6 - Numbers which are divisible by 30

Total number of 4 digit numbers = 9999 - 999 = 9000
Number of 4 digit numbers divisible by 6 = 9000/6 = 1500
Number of 4 digit numbers divisible by 30 = 9000/30 = 300

Required numbers = 1500 - 300 = 1200.

Hence, option (c).

Answer: Option D

Explanation :

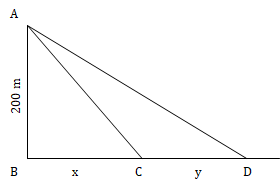
At 11 am, the car is at C and Ayesha is at A.
In △ABC, angle ACB = 45°
Tan45° = 1 = $\frac{\mathrm{AB}}{\mathrm{BC}}$
⇒ BC = AB = 200

At 11:02 am, the car is at D and Ayesha is at A.
In △ABD, angle ADB = 30°
Tan30° = $\frac{1}{\sqrt{3}}$ = $\frac{\mathrm{AB}}{\mathrm{BD}}$
⇒ BD = AB√3 = 200√3

⇒ CD = 200√3 - 200 = 200(√3 - 1) = 200(0.732) = 146.4 m

∴ The car moved 146.4 m in 2 minutes.

⇒ Speed of the car = $\frac{0.1464 \mathrm{kms}}{{\displaystyle \raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$60$}\right.} \mathrm{hours}}$ = 4.392 kmph.

Hence, option (d).

Answer: Option D

Explanation :

Alex and Dilip work together on Tuesday and Wednesday while the other working day differs for them.

Alex and Dilip will not work on Monday and Thursday, since no one works for 3 consecutive days.

​​​​​​​

Cathy does not work on Saturday and Monday but she needs to work on 2 consecutive days. This is possible when Cathy works on Thursday and Friday. The 3rd day Cathy works should not be consecutive, hence it can only be Sunday.

Now, Cathy does not work with Alex, hence the 3rd day Alex works can only be Saturday. Dilip and Bhabha do not work with Alex on this day.

​​​​​​​

2 people need to work on Monday, these 2 people can only be Bhabha and Ethan.

The 2nd person to work on Saturday can only be Ethan.

Since Ethan should work for 2 consecutive days but not 3, Ethan should work on Friday as well.

​​​​​​​

Now, Bhabha needs to work on 3 days. This is possible when Bhabha works on Sunday and Thursday.

3 people need to work on Sunday hence Dilip works on Sunday.

​​​​​​​

[Note: Since they are working on all 7 days throughout the year, B works on two consecutive days i.e., Sunday & Monday]

Bhabha and Cathy work together for 2 days i.e., on Thursday and Sunday.

Hence, option (d).

Answer: Option D

Explanation :

Consider the solution to first question of this set.

​​​​​​​

Dilip and Ethan do not work together on any of the days.

Hence, option (d).

Answer: Option D

Explanation :

Consider the solution to first question of this set.

​​​​​​​

Alex works on Saturday.

Hence, option (d).

Answer: Option C

Explanation :

Consider the solution to first question of this set.

​​​​​​​

Ethan works consecutively on Friday and Saturday.

Hence, option (c).

Answer: Option A

Explanation :

Consider the solution to first question of this set.

​​​​​​​

Bhabha, Cathy and Dilip work on Sunday.

Hence, option (a).