IPMAT (I) 2019 QA MCQ | Previous Year IPMAT - Indore Paper
If the compound interest earned on a certain sum for 2 years is twice the amount of simple interest for 2 years, then the rate of interest per annum is _______ percent
- A.
200%
- B.
2%
- C.
4%
- D.
400%
Answer: Option A
Explanation :
Workspace:
The maximum value of the natural number n for which 21n divides 50! is
- A.
6
- B.
7
- C.
8
- D.
9
Answer: Option C
Explanation :
21 = 3 × 7
Now, to calculate highest power of a prime number p in N!, we add all the quotients when N is successively divided by p.
So, highest power of 3 in 50! is:
Q(50/3) = 16
Q(16/3) = 5
Q(5/3) = 1
∴ Highest power of 3 in 50! = 16 + 5 + 1 = 22
So, highest power of 7 in 50! is:
Q(50/7) = 7
Q(7/7) = 1
∴ Highest power of 7 in 50! = 7 + 1 = 8
So when 50! is written in prime factorised form it will be:
⇒ 50! = 322 × 78 [There will be power of other prime numbers as well but that is immaterial for this question]
⇒ 50! = 314 × 38 × 78
⇒ 50! = 314 × (3 × 7)8
⇒ 50! = 314 × 218
∴ Highest power of 21 in 50! is 8, hence 218 can divided 50!.
Hence, option (c).
Workspace:
The remainder when is divided by 9 is
- A.
1
- B.
2
- C.
3
- D.
4
Answer: Option B
Explanation :
Workspace:
Placing which of the following two digits at the right end of 4530 makes the resultant six digit number divisible by 6,7 and 9?
- A.
96
- B.
78
- C.
42
- D.
54
Answer: Option A
Explanation :
Workspace:
In a school 70% of the boys like cricket and 50% like football. If x% like both Cricket and Football, then
- A.
20 ≤ x ≤ 50
- B.
x ≤ 20
- C.
x ≥ 50
- D.
10 ≤ x ≤ 70
Answer: Option A
Explanation :
Workspace:
In a class of 65 students 40 like cricket, 25 like football and 20 like hockey. 10 students like both cricket and football, 8 students like football and hockey and 5 students like all three sports. If all the students like at least one sport, then the number of students who like both cricket and hockey is
- A.
7
- B.
8
- C.
10
- D.
12
Answer: Option A
Explanation :
Workspace:
If x ∈ (a, b) satisfies the inequality ≥ 1, then the largest possible value of b - a is
- A.
3
- B.
1
- C.
2
- D.
No real values of x satisfies the inequality
Answer: Option B
Explanation :
Workspace:
If a, b, c are real numbers a2 + b2 + c2 = 1, then the set of values ab + bc + ca can take is:
- A.
[-1, 2]
- B.
[-1/2, 2]
- C.
[-1, 1]
- D.
[-1/2, 1]
Answer: Option D
Explanation :
Workspace:
The inequality < 1 holds true for
- A.
x ∈ (1/3, 1)
- B.
x ∈ (1/3, 2)
- C.
x ∈ (0, 1/3) ∪ (1, 2)
- D.
x ∈ (-∞, 1)
Answer: Option A
Explanation :
Workspace:
The set of values of x which satisfy the inequality < 0.343 is
- A.
(1/2, 1)
- B.
(1/2, ∞)
- C.
(-∞, 1/2)
- D.
(-∞, 1/2) ∪ (1, ∞)
Answer: Option D
Explanation :
Workspace:
A chord is drawn inside a circle, such that the length of the chord is equal to the radius of the circle. Now, two circles are drawn, one on each side of the chord, each touching the chord at its midpoint and the original circle. Let k be the ratio of the areas of the bigger inscribed circle and the smaller inscribed circle, then k equals
- A.
2 + √3
- B.
1 + √2
- C.
7 + 4√3
- D.
97 + 56√3
Answer: Option D
Explanation :
Workspace:
Points P, Q, R and S are taken on sides AB, BC, CD and DA of square ABCD respectively, so that AP : PB = BQ : QC = CR : RD = DS : SA = 1 : n . Then the ratio of the area of PQRS to the area of ABCD is
- A.
1 : (1 + n)
- B.
1 : n
- C.
1 + n2 : (1 + n)2
- D.
(1 + n) : (1 + n2)
Answer: Option C
Explanation :
Workspace:
On a circular path of radius 6 m a boy starts from a point A on the circumference and walks along a chord AB of length 3 m. He then walks along another chord BC of length 2 m to reach point C. The point B lies on the minor arc AC. The distance between point C from point A is
- A.
(√15 + √35)/2 m
- B.
8 m
- C.
√13 m
- D.
6 m
Answer: Option A
Explanation :
Workspace:
The area enclosed by the curve 2|x| + 3|y| = 6 is
- A.
12 sq. units
- B.
3 sq. units
- C.
4 sq. units
- D.
24 sq. units
Answer: Option A
Explanation :
2|x| + 3|y| = 6
Case 1: x > 0 and y > 0 [Quandrant I]
⇒ 2x + 3y = 6
Case 2: x < 0 and y > 0 [Quandrant II]
⇒ - 2x + 3y = 6
Case 3: x < 0 and y < 0 [Quandrant III]
⇒ - 2x - 3y = 6
Case 4: x > 0 and y < 0 [Quandrant IV]
⇒ 2x - 3y = 6
Each of these 4 lines can be drawn in their respective quadrants as shown in the figure.
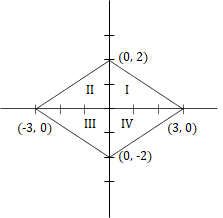
Area of region I = 1/2 × 3 × 2 = 3 sq. units
Similarly area of region II, III and IV = 3 sq. units each.
∴ Area of all the 4 regions combined = 3 + 3 + 3 + 3 = 12 sq. units
Hence, option (a).
Workspace:
Two points on a ground are 1 m apart. If a cow moves in the field in such a way that it's distance from the two points is always in ratio 3: 2 then
- A.
the cow moves in a straight line
- B.
the cow moves in a circle
- C.
the cow moves in a parabola
- D.
the cow moves in a hyperbola
Answer: Option B
Explanation :
Workspace:
Given that cos x + cos y = 1, the range of sin x - sin y is
- A.
[-1, 1]
- B.
[-2, 2]
- C.
[0, √3]
- D.
[-√3, √3]
Answer: Option D
Explanation :
Workspace:
If sinθ + cosθ = m, then sin6θ + cos6θ equals
- A.
3(m2 + 1)/4
- B.
3(m2 - 1)/4
- C.
1 - 3(m2 - 1)/4
- D.
1 - 3(m2 - 1)2/4
Answer: Option D
Explanation :
Given, sinθ + cosθ = m
Taking square boths sides we get
sin2θ + cos2θ + 2 × sinθ × cosθ = m2
⇒ 1 + 2 × sinθ × cosθ = m2
⇒ sinθ × cosθ = (m2 - 1)/2 ...(1)
Now we need to find the value of sin6θ + cos6θ
= (sin2θ)3 + (cos2θ)3
= (sin2θ + cos2θ)(sin4θ + cos4θ - sin2θ × cos2θ)
= 1 × ((sin2θ + + cos2θ)2 - 2 × sin2θ × cos2θ - sin2θ × cos2θ)
= ((1)2 - 3 × sin2θ × cos2θ)
= (1 - 3 × sin2θ × cos2θ)
= (1 - 3 × ((m2 - 1)/2)2)
= (1 - 3 × (m2 - 1)2/4)
Hence, option (d).
Workspace:
If inverse of the matrix is , then the value of x is
- A.
0.5
- B.
1
- C.
2
- D.
3
Answer: Option A
Explanation :
Workspace:
The function f(x) = is
- A.
positive and monotonically increasing for x ∈ and x ∈
- B.
negative and monotonically decreasing for x ∈ and x ∈
- C.
negative and monotonically increasing for x ∈ and positive and monotonically increasing x ∈
- D.
positive and monotonically increasing for x ∈ and negative and monotonically decreasing x ∈
Answer: Option C
Explanation :
Workspace:
For a > b > c > 0, the minimum value of the function f(x) = |x - a| + |x - b| + |x - c| is
- A.
2a- b - c
- B.
a + b - 2c
- C.
a + b + c
- D.
a - c
Answer: Option D
Explanation :
Workspace:
Let α, β be the roots of x2 - x + p = 0 and γ, δ be the roots of x2 - 4x + q = 0 where p and q are integers. If α, β, γ, δ are in geometric progression then
- A.
-34
- B.
30
- C.
26
- D.
-38
Answer: Option A
Explanation :
Workspace:
If (1 + x - 2x2)6 = A0 + , then value of A2 + A4 + A6 + ... + A12 is
- A.
31
- B.
32
- C.
30
- D.
29
Answer: Option A
Explanation :
Workspace:
The number of terms common to both the arithmetic progressions 2,5,8,11,...., 179 and 3,5,7,9,....., 101 is
- A.
17
- B.
16
- C.
19
- D.
15
Answer: Option A
Explanation :
Workspace:
From a pack of 52 cards, we draw one by one, without replacement. If f(n) is the probability that an Ace will appear at the nth turn, then
- A.
f(2) = 1/13 > f(3)
- B.
1/13 > f(2) > f(3)
- C.
f(3) > f(2) = 1/13
- D.
f(2) = f(3) = 1/13
Answer: Option D
Explanation :
Workspace:
A die is thrown three times and the sum of the three numbers is found to be 15. The probability that the first throw was a four is
- A.
1/6
- B.
1/4
- C.
1/5
- D.
1/10
Answer: Option C
Explanation :
Workspace:
In a given village there are only three sizes of families: families with 2 members, families with 4 members and families with 6 members. The proportion of families with 2,4 and 6 members are roughly equal. A poll is conducted in this village wherein a person is chosen at random and asked about his/her family size. The average family size computed by sampling 1000 such persons from the village would be closest to
- A.
4
- B.
4.667
- C.
4.333
- D.
3.667
Answer: Option B
Explanation :
Workspace:
The value of log330−1 + log4900−1 + log530−1 is
- A.
0.5
- B.
30
- C.
2
- D.
1
Answer: Option D
Explanation :
Workspace:
The inequality logaf(x) < logag(x) implies that
- A.
f(x) > g(x) > 0 for 0 < a < 1 and g(x) > f(x) > 0 for a > 1
- B.
g(x) > f(x) > 0 for 0 < a < 1 and f(x) > g(x) > 0 for a > 1
- C.
f(x) > g(x) > 0 for a > 0
- D.
g(x) > f(x) > 0 for a > 0
Answer: Option A
Explanation :
Workspace:
Three cubes with integer edge lengths are given. It is known that the sum of their surface areas is 564 cm2 Then the possible values of the sum of their volumes are
- A.
764 cm3 and 586 cm3
- B.
586 cm3 and 564 cm3
- C.
764 cm3 and 564 cm3
- D.
586 cm3 and 786 cm3
Answer: Option A
Explanation :
Workspace:
Determine the greatest number among the following four numbers
- A.
2300
- B.
3200
- C.
2100 + 3100
- D.
4100
Answer: Option B
Explanation :
Workspace:
The number of points, having both co-ordinates as integers, that lie in the interior of the triangle with vertices (0, 0), (0, 31), and (31, 0) is
- A.
435
- B.
465
- C.
450
- D.
464
Answer: Option A
Explanation :
Workspace:
Two small insects, which are x metres apart, take u minutes to pass each other when they are flying towards each other, and v minutes to meet each other when they are flying in the same direction. Then, the ratio of the speed of the slower insect to that of the faster insect is
- A.
u/v
- B.
u/(v - u)
- C.
(v - u)/(v + u)
- D.
u/(v + u)
Answer: Option C
Explanation :
Workspace:
An alloy P has copper and zinc in the proportion of 5: 2 (by weight), while another alloy Q has the same metals in the proportion of 3: 4 (by weight). If these two alloys are mixed in the proportion of a : b (by weight), a new alloy R is formed, which has equal contents of copper and zinc. Then, the proportion of copper and zinc in the alloy S, formed by mixing the two alloys P and Q in the proportion of b : a (by weight) is
- A.
7 : 9
- B.
9 : 7
- C.
9 : 5
- D.
5 : 9
Answer: Option C
Explanation :
Workspace:
How many different numbers can be formed by using only the digits 1 and 3 which are smaller than 3000000 ?
- A.
64
- B.
128
- C.
190
- D.
254
Answer: Option C
Explanation :
Workspace:
There are numbners a1, a2, a3,…,an each of them being +1 or -1. If it is known that a1a2 + a2a3 + a3a4 + …an−1an + ana1 = 0 then
- A.
n is a multiple of 2 but not a multiple of 4
- B.
n is a multiple of 3
- C.
n can be any multiple of 4
- D.
The only possible value of n is 4
Answer: Option C
Explanation :
Workspace:
Analyze the given data for exports and imports of rubber in Rs. crores from 2016 to 2017 and answer the questions based on the analysis.
Average annual exports for the given period 2006-2017) was approximately
- A.
Rs. 230 cr.
- B.
Rs. 220 cr.
- C.
Rs. 210 cr.
- D.
Rs. 190 cr.
Answer: Option B
Explanation :
Workspace:
The percentage decline in exports during the period 2006-2011 is more than the percentage decline in exports during 2012-2017 by approximately
- A.
16.5
- B.
20.5
- C.
12.5
- D.
21.5
Answer: Option A
Explanation :
Workspace:
The maximum difference between imports and exports is
- A.
Rs. 60 cr.
- B.
Rs. 110 cr.
- C.
Rs. 120 cr.
- D.
Rs. 100 cr.
Answer: Option C
Explanation :
Workspace:
Balance of trade is defined as imports subtracted from exports ( = exports - imports). Which of the following blocks of three years has witnessed the largest average negative balance of trade?
- A.
2007 - 09
- B.
2015 - 17
- C.
2014 - 16
- D.
2010 - 12
Answer: Option D
Explanation :
Workspace:
 Solution
Solution Discuss
Discuss Report
Report