IPMAT (I) 2021 QA MCQ | Previous Year IPMAT - Indore Paper

Answer: Option A

Explanation :

f(x + xy) = f(x) + f(xy)

Substituting y = 1
⇒ f(x + x) = f(x) + f(x)
⇒ f(2x) = 2f(x)

Substituting y = 2
⇒ f(x + 2x) = f(x) + f(2x)
⇒ f(3x) = f(x) + 2f(x)
⇒ f(3x) = 3f(x)

Hence, we can say, f(ax) = a × f(x)   ...(1)

Substituting a = 2020 and x = 1
⇒ f(2020) = 2020 × f(1)
⇒ 1 = 2020 × f(1)
⇒ f(1) = 1/2020

Now, putting x = 1 and a = 2021 in (1) we get,
f(2021) = 2021 × f(1) = 2021/2020

Hence, option (a).

Answer: Option C

Explanation :

Given, log₂[log₃(log₄a)] = log₃[log₄(log₂b)] = log₄[log₂(log₃c)] = 0

⇒ log₂[log₃(log₄a)] = 0
⇒ log₃(log₄a) = 2⁰ = 1
⇒ log₄a = 3¹ = 3
⇒ a = 4³ = 64

Also, log₃[log₄(log₂b)] = 0
⇒ log₄(log₂b) = 3⁰ = 1
⇒ log₂b = 4¹ = 4
⇒ b = 2⁴ = 16

Also, log₄[log₂(log₃c)] = 0
⇒ log₂(log₃c) = 4⁰ = 1
⇒ log₃c = 2¹ = 2
⇒ c = 3² = 9

∴ a + b + c = 64 + 16 + 9 = 89.

Hence, option (c).

Answer: Option A

Explanation :

In an AP S of odd number of terms = n × (Middle term)

Given, S₅ = S₉ 

⇒ 5 × a₃ = 9 × a₉

⇒ a₃ : a₉​​​​​​​ = 9 : 5

Hence, option (a).

Answer: Option A

Explanation :

Given,  2A - B - A(A + B)^-1A + B(A + B)^-1B

= 2A - B - (A + B)^-1[A² - B²]

= 2A - B - (A + B)^-1(A - B)(A + B)

= 2A - B - (A + B)^-1(A + B)(A - B)

= 2A - B - I(A - B)

= 2A - B - (A - B)

= 2A - B - A + B

= A 

Hence, option (a).

Answer: Option A

Explanation :

Let the three angle of the triangle be A = a - d, B = a and C = a + d degrees.
⇒ A + B + C = (a - d) + a + (a + d) = 180°
⇒ a = 60°

∴ B = 60°

Now, Sin(2A + B) = 1/2
Since, B = 60° (2A + B) > 60°
Sin30° = 1/2 or Sin(180 - 30) = 1/2
⇒ 2A + B = 180 - 30 
⇒ 2A + 60° = 150°
⇒ A = 45°

∴ C = 180 - 45 - 60 = 75°

∴ Sin(B + 2C) = Sin(210°)
= Sin(180° + 30°)
= - Sin(30°)
= - 1/2

Hence, option (a).

Answer: Option A

Explanation :

Unit's digit of (743)⁸⁵ = Unit's digit of 3⁸⁵ 
= Unit's digit of (3⁴)²¹ × 3 = 1 × 3 = 3 [Unit's digit of 3⁴ = 1]

Units's digit of (525)³⁷ = Units's digit of 5³⁷ = 5

Units's digit of (987)⁹⁶​​​​​​​ = Units's digit of 7⁹⁶ 
= Units's digit of (7⁴)²⁴ = 1 [Unit's digit of 7⁴ = 1]

∴ Unit's digit of (743)⁸⁵ – (525)³⁷ + (987)⁹⁶ = 3 - 5 + 1 = -1 = 9

Hence, option (a).

Answer: Option C

Explanation :

The set of all real value of p for which the equation 3sin²x + 12cosx – 3 = p has one solution is

Given, 3sin²x + 12cosx – 3 = p
⇒ 3(1 - cos²x) + 12cosx – 3 = p
⇒ -3cos²x + 12cosx – p = 0
⇒ -3[cos²x - 4cosx] – p = 0
⇒ -3[cos²x - 4cosx + 4] + 12 – p = 0 [Adding and subtracting 12]
⇒ -3[cosx - 2]² = p - 12
⇒ [cosx - 2]² = -p/3 + 4

Now, 1 ≥ cosx ≥ -1
∴ 9 ≥ (cosx - 2)² ≥ 1
⇒ 9 ≥ -p/3 + 4 ≥ 1
⇒ 5 ≥ -p/3 ≥ -3
⇒ -15 ≤ p ≤ 9

Hence, option (c).

Answer: Option B

Explanation :

Area of triangle AOB = 4, DOC = 9, AOD = x and BOC = y

​​​​​​​

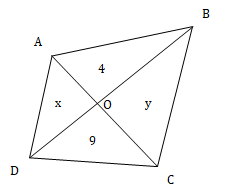
In a quadrilateral, product of area of diagonally opposite triangles is same.

∴ 4 × 9 = x × y
⇒ xy = 36

Area of quadrilateral = 4 + 9 + x + y
Now we need to minimise 4 + 9 + x + y
This is possible when x + y is least possible.

We know, AM ≥ GM
⇒ $\frac{(x + y)}{2}$ ≥ $\sqrt{xy}$
⇒ (x + y) ≥ 12
∴ Least possible value of x + y = 12

⇒ Least possible area of the quadrilateral = 4 + 9 + x + y = 25

Hence, option (b).

Answer: Option A

Explanation :

The highest possible value of the ratio of a four-digit number and the sum of its four digits is

Let the number be 'abcd' = 1000a + 100b + 10c + d

We have to find the highest possible value of 
(1000a + 100b + 10c + d) : (a + b + c + d)

This is possible when a is highest and b, c and d are lowest
i.e., a = 9 and b = c = d = 0

∴ Highest possible ratio = 9000 : 9 = 1000

Hence, option (a).

Answer: Option B

Explanation :

g(x) = -2x passes through (a, b)
⇒ b = -2a   ...(1)

Now, f(x) = ax² + bx + c
⇒ f(x) = ax² - 2ax + c   [from (1)]

f(x) passes through (2, 0)
⇒ a(-2)² - 2a(-2) + c = 0
⇒ 8a + c = 0
⇒ c = -8a

∴ f(x) = ax² - 2ax - 8a

Now, we have to find the least value of f(x) + 9a + 1
= ax² - 2ax - 8a + 9a + 1
= ax² - 2ax + a + 1
= a(x² - 2x + 1) + 1
= a(x - 1)² + 1

Least value of this expression will be 1, when x = 1.

Hence, option (b).

Answer: Option A

Explanation :

Let the number of people who speak

Exactly 3 languages = a
Exactly 2 languages = b
Exactly 1 language = c
No language = d

⇒ a + b + c + d = 100   ...(1)

Given, c = 50 and a + b = 40   ...(2)

From (1) and (2) we get, d = 10   ...(3)

The number of people who cannot speak in any of these three languages is twice the number of people who can speak in all these three languages
⇒ d = 2a​​​​​​​
∴ a = 5 [d = 10 from (3)]

Now, 52% of the population can speak in Hindi and 25% of the population can speak exactly in one language among English and Tamil. We can make the following Venn Diagram with the information so far.

​​​​​​​

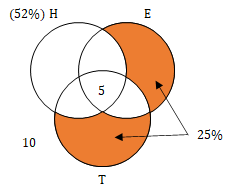
Total orange region = 25

Now, Number of people speaking exactly one language (c) = 50 = (Only Hindi speaking people) + (Only English speaking people) + (Only Tamil speaking people)
⇒ 50 = (Only Hindi speaking people) + 25
⇒ Only Hindi speaking people = 25​​​​​​​

Also, Total Hindi speaking people = Only Hindi + (Hindi and exactly one other language) + (All three languages)
⇒ 52 = 25 + (Hindi and exactly one other language) + 5
⇒ Hindi and exactly one other language = 22

Hence, option (a).

Answer: Option C

Explanation :

Case 1: Train 2 starts 2 hours after Train 1.
Train 1 travels from 12 pm till 8 pm i.e., for 8 hours.
Same distance is travelled by Train 2 from 2 pm till 8 pm i.e., in 6 hours.
∴ Ratio of speeds of Train 1 and Train 2 = 6 : 8 = 3 : 4
⇒ Let speed of Train 1 = 3x and Train 2 = 4x
⇒ 3x + 4x = 140
⇒ x = 20

⇒ Speed of Train 1 = 60 kmph, Speed of Train 2 = 80 kmph.

Case 2: Train 2 starts 5 hours after Train 1.
Train 1 would have travelled 5 × 60 = 300 kms when Train 2 starts i.e., at 5 pm.
Relative speed of the two trains = 80 - 60 = 20 kmph.
∴ Time for Train 2 after it starts to meet Train 1 = 300/20 = 15 hours.

⇒ 15 hours after 5 pm = 8 am the next day.

Hence, option (c).

Answer: Option C

Explanation :

Let the five digit number be 'abcde'

All digits are distinct and digits a, c and e must be odd

There are 5 odd digits i.e., 1, 3, 5, 7 and 9.
a can take any of these 5 digits in 5 ways.
c can take any of the remaining 4 digits in 4 ways.
e can take any of the remaining 3 digits in 3 ways.
∴ Number of ways of choosing values for a, c and e = 5 × 4 × 3 = 60 ways.

b and d can take distinct values out of 0, 2, 4, 6, 8 and remaining 2 odd digits in 7 × 6 = 42 ways.

∴ Total number of ways of forming the requried 5 digit number = 60 × 42 = 2520 ways.

Hence, option (c).

Answer: Option D

Explanation :

Total number of lines that can be formed using 10 points = ¹⁰C₂ = 45 lines.

But out of these 10, 5 points are collinear and hence will give only 1 line instead of ¹⁰C₂ = 10.

∴ Number of unique lines = 45 - 10 + 1 = 36.

Hence, option (d).

Answer: Option D

Explanation :

The intersection of the lines x + 2y = 4 and 2x + 3y = 6 is (0, 2)

Slope of line 3x – y = 2 is 3. Slope of line perpendicular to this line is -1/3 [Product of slopes of two perpendicular lines = -1]

Now, we need to find the x-intercept of a line passing through (0, 2) whose slope is -1/3

Let the x-intercept be (a, 0)

⇒​ Slope of the line passing through (a, 0) and (0, 2) = - 1/3

⇒​ $\frac{0-2}{\mathrm{a}-0}$ = $-\frac{1}{3}$

⇒​ a = 6

Hence, option (d).

Answer: Option D

Explanation :

Total number of matches played = ⁶C₂ = 15
Each team plays 5 matches, one against each of the remaining 5 teams.

Points distributed in a match = 2 (2 + 0 or 1 + 1)
Total points to be distributed in the tournament = 2 × 15 = 30 points.
So far points scored by A, B, C and D = 8 + 6 + 5 + 5 = 24
∴ Points scored by E and F together = 30 – 24 = 6.

E: E lost only 1 match. The minimum number of points E can score is when it draws its remaining matches i.e., 4 points. Since E and F scored less than 5 points hence, E’s score is 4 point when it draws its remaining 4 matches.

A: A did not lose any game, hence it can score 8 points only by winning 3 matches and drawing 2 matches.

B: B lost 2 matches, hence it can score 6 points only by winning the remaining 3 matches.

C: C lost 2 games, hence it can score 5 points only by winning 2 matches and drawing 1 match.

D: D lost only 1 game, hence it can score 5 points by drawing 3 matches and winning 1 match.

So far A, B, C, D and E together have won 9 matches and lost only 6 matches. But the number of wins should be equal to number of loses.
∴ F must have lost 3 matches more than it wins.

F: Since E’s score is 4, F’s score = 6 – 4 = 2 points. F lost 3 matches more than it won. This is possible in 2 cases.

Case (a): F won 1 match and lost 4 matches and 0 draws.
Since E has to play 4 draws, E will play a draw match against F. [E cannot play drawn against B. B has 0 draws.]
Hence, F cannot have 0 draws.
∴ This case is rejected.

Case (b): F won 0 match and lost 3 matches and drew 2 matches.
This is the only possible case.

We can make the following table with the information available.

​​​​​​​

Sum of the draws column = 12 hence there are total 6 drawn matches. [Each draw results in entry of draw for 2 teams.]

Hence, option (d).

Answer: Option D

Explanation :

Consider the solution to first question of this set.

E plays the highest number of draws i.e., 4 draws.

Hence, option (d).

Answer: Option C

Explanation :

Consider the solution to first question of this set.

F scored 2 points.

Hence, option (c).

Answer: Option C

Explanation :

Consider the solution to first question of this set.

D lost only 1 match to C, hence A cannot defeat D.

Hence, option (c).

Answer: Option C

Explanation :

Consider the solution to first question of this set.

E played 4 draws and lost 1 match. Since B didn't play any draw, the match between B and E must end in a result. Hence, B must have defeated E.

Hence, option (c).