IIFT 2020 QA | Previous Year IIFT Paper
Previous year paper questions for IIFT 2020 QA
Maruti-Suzuki Company manufactures the Ciaz cars at its Manesar facility. The company employs labour and capital/machine as inputs in a 2 : 1 ratio of their quantities. The cost of one unit of labour (think it as wage per hour) is 500 rupees and the cost of one unit of capital (machine running cost per hour) is 1500 rupees. The total labour and capital cost for the monthly production is 5 crore rupees.
Due to economic slowdown, the company has decided to reduce monthly production to half.
Meanwhile, the labour cost has decreased by 20% and the capital cost has gone up by 20%. Find the total capital and labour cost the company would now incur for the monthly production.
- A.
2.4 crores
- B.
2.6 crores
- C.
2.8 crores
- D.
3 crores
Answer: Option B
Explanation :
Let the labour employed by the company be 2x and the capital be x.
Thus, the total cost of running production for an hour = 500 × 2x + 1500 × x = 2500x
Total cost for running the production for a month = 5 Crores = 5 × 107
Total number of hours the production is done = x = = 20000
Since the production is cut in half, the total hours = 0.5 × = 20000 = 10000
Labour costs decreased by 20% and the capital cost increased by 20%.
Thus, the total cost per hour = 500 × 2x × 0.8 + 1500 × x × 1.2 = 2600x
Since x = 10000, the total cost = 2600 × 100000 = 2.6 Crores.
Hence, the answer is option B.
Workspace:
Refer to the figure given below. AB, CD and EF are three parallel paths. A person starts from AB to reach EF by moving in four steps - moving from AB to O1 in step 1, from O1 to CD in step 2, from CD to O2 in step 3 and from O2 to EF in step 4. If he takes a curved path in one step, he cannot take a curved path in the next step. In how many ways the person can reach EF from AB?

- A.
128
- B.
256
- C.
32
- D.
64
Answer: Option A
Explanation :
The total number of possible ways from AB to EF = 4 × 4 × 4 × 4 = 256
If a curved path is taken in a step, then the next step cannot be a curved path.
Let C denotes a curved path and S denotes a straight path.
Thus, the invalid paths are as follows: CCCC, CCCS, CCSC, CSCC, SCCC, CCSS, SCCS, SSCC. Thus, a total of 8 paths.
Total number of arrangements for these 8 paths = 8 × 2 × 2 × 2 × 2 = 128
Thus, the total number of valid paths = 256 - 128 = 128
Hence, the answer is option A.
Workspace:
The product of the roots of the equation + = 2 is approximately equal to:
- A.
22
- B.
-27
- C.
35
- D.
-33
Answer: Option D
Explanation :
Cubing the given equation, we have:
(a + b)3 = a3 + b3 + 3 ∙ a ∙ b(a + b)
11 + 2x + 11 - 2x + 3 ∙ (a + b)
Given a + b = 2.
Hence:
22 + 3 ∙ (2)
= 22 + 6 × = 8
Cubing this we get: 121 - 4x2 =
4x2 = 121 + =
x2 = 33.42
One root would be + and the other -.
The product of the roots would be approximately -33.
Workspace:
Sumit stays in Noida in a joint family comprising of his parents, uncle, aunt, an elder sister and a cousin two years younger than him. Sumit completed his MBA in 2013, from a reputed B-School.
That year, the average age of Sumit's family was 41. Sumit got married in 2015 and two years after he became father. If the average age of Sumit's family in 2019 remains same as in 2013, and Sumit is older than his wife by 3 years, at what age did Sumit graduate MBA?
- A.
31
- B.
35
- C.
38
- D.
41
Answer: Option B
Explanation :
Let Sumit's age at the time of graduating MBA [in 2013] be years. Thus, his wife's age that year will be X - 3 years.
The average age of the family in 2013 = 41 years.
Thus, the total age of the family in 2013 = 7 x 41 = 287
Sumit got married in 2015. Thus, his wife's age in 2015 will added to the family's total.
The total age of family in 2015 = 287 + 14 + - 3 + 2 = X + 300
In 2017, Sumit had a daughter.
The total age of the family in 2017 = X + 300 + 8(2) = X + 316
The total age of the family in 2019 = X + 316 + 9(2) = X + 334
We are given that the average age of the family in 2019 is the same as that in 2013.
Thus, X + 334 = 41 x 9 = 369
X = 369 - 334 = 35 years
Thus, the age of Sumit at the time of graduating MBA is 35 years.
Hence, the answer is option B.
Workspace:
A fruit seller in a locality uses dishonest practice as follows:
(i) He cheats on weight by 10 percent for every 1kg weight.
(ii) He pushes up the price of fruit by 15 percent and then gives a discount of 8 percent to the buyers for every kg sold.
Find the percentage profit of the fruit seller from sale of 1kg. (Profit is defined as Revenue - Cost)
- A.
18.95
- B.
17.56
- C.
16.04
- D.
15.00
Answer: Option B
Explanation :
Let the cost of fruit be Rs. 100 for 1000gm.
The fruit seller marks the price by 15% and then gives a discount of 8%. Thus, the selling price of fruit = Rs. 105.8
The fruit seller also cheats the customers by 10% of the weight. Thus, he sells 900gm for Rs. 105.8
Cost Price = = Rs. 100/kg
Selling price = = Rs. 117.56
Percentage profit = × 100 = 17.56%
Hence, the answer is option B.
Workspace:
If 16x = and 9x = , then the values of x and y are respectively,
- A.
and
- B.
and
- C.
and
- D.
and
Answer: Option C
Explanation :
From the first equation: 16x ∙ 256y = 64 ⇒ 42x ∙ 44y = 43
Comparing powers: 2x + 4y = 3 .....(A)
From second equation: 32x + y = 32
Comparing powers: 2x + y = 2 ......(B)
Solving A and B, we get option C as answer
Workspace:
Mr. Madhukar worked for 5 years in a multi-commodity trading company after graduating from a reputed B-School. He then resigned from his job and started an online garment export business. For his business Madhukar used Rs. 8,00,000/- of his own savings and borrowed Rs. 12,00,000/- from a private sector bank in April, the beginning month of the financial year. Mean while, RBI eased repo rate in May and banks passed on the benefits to the borrowers. As a result, Madhukar borrowed an additional Rs. 9,00,000/- after 4 months at an interest rate which is 10% lower than the interest rate of his earlier borrowing. If the total interest paid by Madhukarat the end of that year on both the loans is Rs. 1,39,200/-, what is the interest rate per annum on first borrowing?
- A.
6%
- B.
7%
- C.
8%
- D.
9%
Answer: Option C
Explanation :
Let the rate of interest of first borrowing be R% p.a.
The principal of first borrowing is kept for an entire 12 month span.
Hence, simple interest payable on it at end of financial year = (12,00,000*1*R)/100 = 12,000*R rupees
Now, rate of second borrowing = 0.9R % p.a.
The principal of second borrowing is kept for 8 months total till financial year end.
Hence, simple interest payable on it at end of financial year = (9,00,000*R*8)/(12*100) = 5400R rupees
Now, 12000R + 5400R = 1,39,200
Hence, R = 8% p.a.
Workspace:
In the figure, a circle of radius 2 cm is inscribed in a square. There are four smaller circles at each of the cornerof the square. Whatis the total area covered by all the five circles?
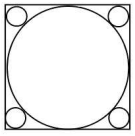
- A.
4π + 4π(6 - 4)2 cm2
- B.
4π + 4π(3 - 2)2 cm2
- C.
4π + 4π(12 - 8)2 cm2
- D.
4π + 4π(9 - 6)2 cm2
Answer: Option A
Explanation :
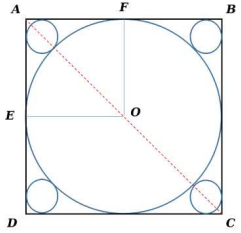
It has been given that radii OE = OF = 2 cm. Consequently, AB = 4 cm {side of the square}. AC = 4√2 cm
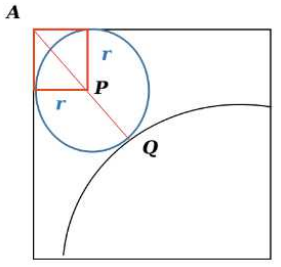
Further, let the radius of the smaller circles be r cm. Then, AP = r√2 cm. Thus, AQ = r√2 + r or r(√2 + 1) cm.
There are two such regions on line AC. Hence, we can rewrite AC = 2 × r(√2 + 1) + 4. This is equal to 4√2 cm. On equating, we obtain r = (6 - 4√2) cm.
We have been asked to find the total area covered by the five circles = 4π + 4 × π(6 - 4√2)2 cm2
Hence, Option A is the correct choice.
Workspace:
Surojit Ghosh left his IT job last year and started a food business with his wife Debjani. They named the business "Bong's Kitchen". Surojit takes hours more when he works alone compared to when
he works jointly with his wife. On the other hand, Debjani takes 28 hours more than what she takes
when she works with Surojit. How long approximately will it take, Surojit to complete the business
work alone ?
- A.
6 hours
- B.
9 hours
- C.
12 hours
- D.
15 hours
Answer: Option D
Explanation :
Let the number of hours needed by Surojit working alone be S hours and the number of hours required by Debjani when she works alone be D.
The time required to finish the work when they work together =
Hence, we can frame the given 2 conditions as:
S - = ...(1)
D - = ..(2)
Solving the two equations simultaneously, we get S = 15 hours approx
Workspace:
Three friends Pradeep, Suresh and Subodh workin the same office. During an extended weekend they decided to go together on a family trip to Corbett National Park. They started from office in their own car but at different time and travelled in the same direction at speeds of 50 km/hr, 60 km/hr and 75 km/hr respectively. Suresh and Subodh overtook Pradeep at the same point. If Suresh started 90 minutes after Pradeep, how many minutes after Pradeep did Subodh start from the office?
- A.
120
- B.
150
- C.
180
- D.
210
Answer: Option C
Explanation :
Consider the instance when Suresh just starts from the office.
Distance that Pradeep has already covered in that time = 50*1.5 = 75 km
Now, by concept of relative velocity, time taken by Suresh to just overtake Pradeep = 75/(60-50) = 7.5 hours
Hence, the point of overtaking on the route is = 60*7.5 = 450 km from the office
Subodh also overtakes Pradeep at the same point. Pradeep covers this 450 km distance in 9 hours.
Subodh can cover this 450 km in 6 hours.
Hence, Subodh can leave 9 - 6 = 3 hours after Pradeep does.
Workspace:
ABCD is a parallelogram whose diagonals are parallel to the lines 2y - x - 5 = 0 and y + 2x - 7 = 0 respectively.
Then ABCD is -
- A.
Cyclic quadrilateral
- B.
Rectangle
- C.
Cube
- D.
Rhombus
Answer: Option D
Explanation :
The slope of any line parallel to 2y - x - 5 = 0 would be 1/2
The slope of any line parallel to y + 2x - 7 = 0 would be -2
Product of slopes = -1 which shows that these 2 lines would be perpendicular i.e. we have a parallelogram
whose diagonals are perpendicular to each other. This means that the quadrilateral is atleast a rhombus
and it would be a square if we can get info that all sides are equal to each other.
Workspace:
Suhani, an enterprising lady took the loan from M/s Koramattam Finance against her gold ornaments at a simple interest of 12% per annum for 2 years. She, then, loaned 50% of the amount received from M/s Koramattam Finance, to Vishamber at the rate of 16% per annum compounded half yearly for 2 years and the remaining amount to Kalawati at the rate of 12% per annum compounded annually for 2 years. What was the approximate percentage earning of Suhani at the end of 2 years?
- A.
42%
- B.
28%
- C.
50%
- D.
60%
Answer: Option B
Explanation :
Let the original amount of money i.e. Principal taken by Suhani = 2P
The amount of money that she owes back to the loan company at the end of 2 years = 2P + 0.24*2P = 2.48P
Now, she loans amount P to Vishamber.
Amount returned by Vishamber to Suhani under given conditions = P ∙ (1.08)4 = 1.36P
She loans amount P to Kalawati.
Amount returned by Kalawati to Suhani at end of 2 years under given conditions = P ∙ (1.12)2 = 1.2544P
Amount received by Suhani at end of 2 years = 1.36P +1.2544P = 2.8544P
Earning of Suhani = 2.8544P - 2.48P = 0.3744P
Workspace:
A Financial Analyst estimates that the probability that the economy will experience recession in next one year is 30%. He also believes that in case of recession, the probability that his mutual funds will increase in value is 20%. He also believes that if there is no recession the probability that the value of mutual funds will increase in value is 75%. Find the probability that mutualfunds value will increase.
- A.
0.285
- B.
0.525
- C.
0.585
- D.
0.60
Answer: Option C
Explanation :
Probability that recession will happen = 0.3 and probability that value will increase in this case = 0.2
Expected probability of mutual fund value increase in this case = 0.3 * 0.2 = 0.06
Probability that recession will not happen = 1 - 0.3 = 0.7 and probability that value will increase in this case = 0.75
Expected probability of mutual fund value increase in this case = 0.7 * 0.75 = 0.525
Hence, total expected probability that mutual fund value will increase = 0.585
Workspace:
The probabilities of three mutually exclusive outcomes of an experiment 0.25(1 - x), 0.5(1 - 2x) and 0.25(1 + 4x) respectively.
Which of the following holds for the value of x ?
- A.
-0.5 ≤ x ≤ 0.5
- B.
0 ≤ x ≤ 0.5
- C.
-0.75 ≤ x ≤ 0.25
- D.
-0.25 ≤ x ≤ 0.5
Answer: Option B
Explanation :
As all 3 are mutually exclusive, we can assume (in one extreme case) that these 3 form the entire range of probability and hence,
0.25(1 - x) + 0.5(1 - 2x) + 0.25 (1 + 4x) = 1 which gives us x = 0
Hence, x is bound by 0 on one end.
Also, none of the probabilities can be negative as any event probability is atleast 0. Hence, for the second event, we can see that x cnnot be greater than 0.5 hence, x is bounded from 0 to 0.5
Workspace:
Two cities Mathura and Agra, 48 kms apart, are located on the bank of River Yamuna. A motor boat goes from Mathura to Agra and returns back as soon as possible. Yamuna flows at a speed of 6 km/hr.
The motorboat completes the trip from Mathura to Agra and back in not more than 6 hours.
Assuming the motorboat does nothalt at Agra, what should be the minimum speed of motorboatin still water?
- A.
16 km/hr
- B.
18 km/hr
- C.
25 km/hr
- D.
27 km/hr
Answer: Option B
Explanation :
Let the river flow from Mathura to Agra. Let the speed of boat in still water be S kmph
Hence, if journey is to be done in 6 hours, then:
+ = 6
Solving this equation, we get: (S - 18)(S + 2) = 0 which gives us S = 18 kmph
Workspace:
A man, from the foot of the building P, walks towards the building Q. After walking for 2 mts, he finds that buildings P and Q makean angle of elevation of 60° and 30° respectively. If building Q is 1.5 mts high, find the distance between the tops of both buildings P and Q.
- A.
5 mts
- B.
4 mts
- C.
mts
- D.
mts
Answer: Option A
Explanation :
The situation given in the problem can be summarised as:

By 30 - 60 - 90 theorem, we can say that P'M = 4 meters and MQ' = 3 meters
Also, triangle P'MQ' would be a right angled triangle.
Hence, P'Q' would be the hypotenuse of length = root(16 + 9) = 5 meters
Workspace:
At what time between 10.00 AM and 11.00 AM,the minute hand and the hour hand of a watch would make an angle of 180°?
- A.
10.20 AM
- B.
10.22 AM
- C.
10.23 AM
- D.
10.25 AM
Answer: Option B
Explanation :
At exactly 10 AM, angle between the two hands = 60 degrees
Applying the concept of relative velocity, we can say that the minute hand has to travel 180 - 60 = 120 degrees more at a relative velocity of 5.5 degrees/minute
Hence, time taken to make 180 degree angle between the 2 hands = 120/5.5 = 22 minutes
Workspace:
An owner of a grocery shop purchases two varieties of grain. The price of first variety is twice the price of the second one. He mixes both the varieties and sells the mixture at the price of Rs. 28 per kg, making a profit of 25%. If the ratio of first variety of grain and the second variety of grain in the mixture is 2 : 3, find the price of first variety of grain.
- A.
Rs. 16/kg
- B.
Rs. 24/kg
- C.
Rs. 32/kg
- D.
Rs. 64/kg
Answer: Option C
Explanation :
Let the mixture so created to be sold was exactly one kg.
Hence, amount of first variety procured to contribute to this mixture = (2/5)*1000 = 400gm or 0.4 kg
Hence, amount of second variety procured to contribute to this mixture = (3/5)*1000 = 600gm or 0.6 kg
Let the cost price of second variety = Rs. a/kg and hence, cost price of first variety = Rs. 2a / kg
Hence, cost price of the entire mixture = 0.6a + 0.4*2a = 1.4a rupees / kg
Also, the mixture is sold at Rs. 28 per kg and it means a profit of 25% ⇒ CP per kg = Rs. (28/1.25) per kg
Equating both, we get a = 16, hence, price of the first variety = 32 rupees per kg
Workspace:
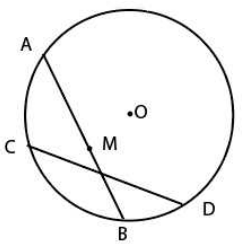
As shown in the diagram, Ram started from point A along the chord AB and Shyam started from D along the chord DC. AB and DC are two equal chords. Ram and Shyam move with the same speed and started at the same time. After some time, Ram reached "M" which is the midpoint of AB.
Ram and Shyam now make an angle at the centre O. If the distance between Ram and Shyam is 6 m now,then how much distance each will walk before they meet each other?
- A.
6√3
- B.
3√3
- C.
2√3
- D.
5√3
Answer: Option C
Explanation :
Using all the information in the question, the given figure becomes as shown below.

Since the perpendiculars from centre to chords of equal lengths are always equal, △OMN becomes an equilateral triangle with MN = 6 m.
In △MNP, PM = PN [by symmetry]
Thus, using the cosine rule,
MN2 = MP2 + NP2 - 2 × MP × NP × cos (120)
36 = MP2 + MP2 + MP2
MP2 = 12
MP = 2√3
Thus, each of them has to travel a distance of 2√3 m in order to meet each other.
Hence, the answer is option C
Workspace:
A circle is inscribed in a right angled isosceles triangle. O is the centre of the circle which touches the triangle ABC at X, Y, Z. If AB = 7√2 cm, then the ratio of AZ : BX : CY -

- A.
1 : (√2 - 1) : 1
- B.
1 : 1 : (√2 - 1)
- C.
1 : 1 : ( - )
- D.
1 : ( - ) : 1
Answer: Option B
Explanation :
If ACB is a right angled isosceles triangle and AB is hypotenuse with length 7*() length, then sides AC and BC = 7 cm
Now, the circle inscribed is an incircle.
Radius of in-circle = {7 + 7 - [7*()]}/2 = 7 -
Now, if center of circle is marked as O, then quadrilateral OZCY is a square.
Hence, CY = CZ = 7 -
Hence, AZ = 7 - 7 - =
Also, BX = BY and BY = BC - CY =
Hence, BX =
Hence, the given ratio becomes 1 : 1 : [() - 1]
Workspace:
Saudi Aramco and Reliance Industries entered into a joint venture where Saudi Aramco invested 20 billion dollars and Reliance Industries invested 30 billion dollars. The ownership ratio is always equal to the investment ratio. After 1 year, the venture made a profit of 6 billion dollars which they reinvested. Now Reliance Industries wants to increase its ownership to 75%, how much it should pay to Saudi Aramco in billion dollars?
- A.
12.4
- B.
8.4
- C.
10.4
- D.
14.4
Answer: Option B
Explanation :
The starting net worth of the venture is 50 billion dollars. After the first year profit of 6 billion dollars is reinvested, the net worth of the venture becomes 56 billion dollars. This is held in the ratio of 2 : 3 by Saudi Aramco and Reliance respectively.
Of this 56 billion dollars, Reliance has a claim to 3/5 th of it i.e. 33.6 billion dollars and Aramco has a claim to 2/5 th of it i.e. 22.4 billion dollars.
Now, Reliance wants to own 75% of this i.e. 3/4th of 56 billion dollars = 42 billion dollars.
To increase its stake from 33.6 to 42 billion dollars, it should pay the difference amount to Aramco i.e. 8.4 billion dollars.
Workspace:
Consider the equation (x - a)(x - b) = 0 which has two identical roots. What should be the condition under which (x - a) (x - b) = c has two distinct real roots?
- A.
c > 0
- B.
a + b > 0
- C.
c(a + b) > 0
- D.
ab > 0
Answer: Option A
Explanation :
(x - a)(x - b) = 0 having identical roots means a = b
Hence, the expression now effectively becomes (x - a)(x - a) = c
For x to have different values, we should have c > 0 because at c = 0, we will end up with x = a AND c < 0 is not possible for rational values of a and x.
For c > 0, we will have x = a + () and x = a - ()
Workspace:
A water tanker can be filled by 2 pipes A & B separately in 16 min & 32 min respectively. Outlet of the tanker is partially open and it can empty the full tanker completely in 1 hour 4 min. Pipes A & B were opened simultaneously for 9 min to fill the tanker but the partially open outlet was not closed. After 9 min the pipes A & B were closed and the tanker then went to Mohan's house, 6 km away to deliver water. If the tanker moved at a constant speed of 36 km/hr, approximately what percentage of tanker was full, when it reached Mohan's house?
- A.
55%
- B.
63%
- C.
58%
- D.
None of the options
Answer: Option A
Explanation :
Let the tank capacity be 64 liters.
Hence, capacity of pipes A and B resp are 4 lit/min and 2 lit/min
Also, the capacity of the draining pipe = -1 lit/min
Now, when all pipes are open for 09 mins, tank filled = (4 + 2)*9 - (9*1) = 45 liters
Now, the tank travels for (6/36)*60 min = 10 minutes
During this time, liquid lost = 10*1 lit/min = 10 liters
Liquid left = 35 liters
hence, percentage filled = 35/64 = 55% approx
Workspace:
An economic survey of total 1000 participants was carried out in Delhi, Mumbai, Kolkata and Chennai about their wealth. 300 participants reported possessing both a house and a car. 500 participants reported possessing both a house and a motorbike. 200 participants reported possessing a house together with a motorbike and a car. Find the number of participants who possess both a house and car, or possess both a house and a motorbike.
- A.
400
- B.
200
- C.
600
- D.
800
Answer: Option C
Explanation :
From the given data, we can create the following diagram:
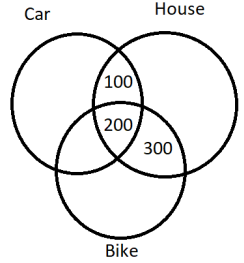
Hence, the required answer = 100 + 200 + 300 = 600
Workspace:
ABC is an isosceles triangle. BDE, EFG, GHI and IJC are four equal isosceles triangles inside ABC triangle. D and F,F and H,H and J are connected by circular arcs. The angle ABC is 30 degrees and BE is 1m. What is the area of the shaded region?
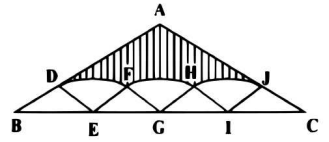
- A.
- m2
- B.
- m2
- C.
- m2
- D.
- m2
Answer: Option C
Explanation :
Since ∠ABC = 30° and ∆DBE is an isosceles triangle, ∠BDE = 120°
Applying the cosine rule in △BDE.
BE2 = BD2 + DE2 - 2 × BD × DE cos(120)
1 = 2BD2 + BD2 [since BD = DE]
BD =
Thus, BD = DE = EF = FG = GH = HI = IJ = JC =
Area of △BDE = × BD × DE × sin(120) = × × × = 4
The total area of all smaller isosceles triangles = 4 × 4 = m2
∠DEF = ∠FGH = ∠HIJ = 120°
Thus, the total area of circular arcs = π × ()2 = m2
Now, side BC = BE + EG + GI + IC = 4m
Using the cosine rule in △ABC, we get AB = AC = .
Thus, Area of △ABC = × × × sin(120) = m2
Thus, the area of the shaded region = Area of △ABC - Area of smaller isosceles triangles - Area of the circular sections
= - - = -
Hence, the answer is option C.
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report