IIFT 23 Dec 2021 QA questions and solutions

1. IIFT 23 Dec 2021 QA | Arithmetic - Time & Work

Rahul takes 4 days to finish one third of a job, Sohan takes 3 days to finish one sixth of thesame work and Ram takes 5 days to finish half the job. All 3 of them together work for 3 days after whichRahul and Ram leave the job. How long will it take for Sohan to complete the remaining work?

A.
6 days
B.
8.1 days
C.
5.1 days
D.
7 days

2. IIFT 23 Dec 2021 QA | Arithmetic - Profit & Loss

A shopkeeper marks up the price of the Toor dal by 20% and gives a discount of 10% to thecustomer. Besides, he also tricks 100 grams to his dealer and his customer respectively while buying orselling 1 kilogram of Toor dal. Find the profit percentage of the shopkeeper.

A.
22%
B.
20%
C.
32%
D.
27%

3. IIFT 23 Dec 2021 QA | Arithmetic - Time, Speed & Distance

For maintaining social distancing due to covid situation, Rohan, Sohan and Rahul are sittingequidistantly, at a distance of 3 meter in a triangular formation. Priya came and sat in between Sohan andRahul such that distance between Priya and Sohan is half the distance between Rahul and Priya. What willbe the distance between Priya and Rohan in meter?

A.
$\sqrt{5}$
B.
$\sqrt{6}$
C.
$\sqrt{7}$
D.
$\sqrt{8}$

Answer: Option C

Explanation :

Considering the data given, Rohan, Sohan, and Rahul are sitting in the shape of an equilateral triangle with sides 3m each. Since Priya's distance from Sohan is half her distance from Rahul, she is sitting at a distance of 1 m from Sohan.

Draw a perpendicular AD on BC.
In △ADC, using the Pythagoras theorem,

AC² = AD² + DC²

3² = AD² + 1.5²

AD = $\frac{3 \sqrt{3}}{2}$

In △ADE, using the Pythagoras theorem,

AE² = AD² + DE²

AE² = $\frac{27}{4}$ + $\frac{1}{4}$ = 7

AE = $\sqrt{7}$

Hence, the answer is option C.

4. IIFT 23 Dec 2021 QA | Arithmetic - Average

In a group of students, x number of students drink only Fruit Juice, 2x number of students drinkonly Coke. $\frac{57}{x}$ students drink both Fruit Juice and Coke and the students who drink neither Fruit Juice norCoke are $\frac{57}{3 x}$ . The number of students who drink Coke may be

A.
41 and 39
B.
39 and 54
C.
59 and 54
D.
41 and 59

5. IIFT 23 Dec 2021 QA | Arithmetic - Percentage

Ishika speaks truth in 60% of cases and Mishika in 85% of cases. Ishika and Mishika agree in astatement. Find the probability that the statement is true.

A.
$\frac{49}{57}$
B.
$\frac{51}{100}$
C.
$\frac{57}{100}$
D.
$\frac{51}{57}$

6. IIFT 23 Dec 2021 QA | Algebra - Simple Equations

The last two digits of the expression 1(1!)^1! + 2(2!)^2! + 3(3!)^3! + .... + 121(121!)^121!

A.
61
B.
71
C.
81
D.
91

7. IIFT 23 Dec 2021 QA | Geometry - Trigonometry

Two towers 10 meters apart, are 4 m and 6 m high respectively. What will be the height of pointof intersection of lines joining the top of each tower to the bottom of opposite tower?

A.
2.2 meters
B.
1.5 meters
C.
5.5 meters
D.
2.4 meters

Answer: Option D

Explanation :

Let AB and CD be the towers of length 4m and 6m respectively.
Let the length of BF be x therefore, the length of FC will be 10-x.
Triangle BEF is similar to triangle BDC

So, $\frac{E F}{D C}$ = $\frac{B F}{B C}$ = $\frac{B E}{B D}$

or, $\frac{E F}{6}$ = $\frac{x}{10}$ = $\frac{B E}{B D}$

Therefore, EF = $\frac{3 x}{5}$

Similarly, triangle EFC is similar to triangle ABC

So, $\frac{E F}{A B}$ = $\frac{C F}{B C}$ = $\frac{E C}{A C}$

or, $\frac{E F}{4}$ = $\frac{10 - x}{10}$ = $\frac{E C}{A C}$

Therefore, $\frac{2 (10 - x)}{5}$ = $\frac{3 x}{5}$

or, x = 4

EF = $\frac{3 x}{5}$ = 2.4 m

8. IIFT 23 Dec 2021 QA | Arithmetic - Ratio, Proportion & Variation

f(x) = $\frac{2 x + 2}{2 x - 2},$ where y = f(x). Find the ratio of x to f(y).

A.
$\sqrt{x}$ : $\sqrt{y}$
B.
x³ : y³
C.
1 : 2
D.
1 : 1

Answer: Option D

Explanation :

f(y) = f(x(x))

or, f(y) = f $(\frac{2 x + 2}{2 x - 2})$

f(y) = $\frac{2 (\frac{2 x + 2}{2 x - 2}) + 2}{2 (\frac{2 x + 2}{2 x - 2}) - 2}$

or, f(y) = $\frac{8 x}{8}$ = x

Therefore x : f(y) = 1 : 1

9. IIFT 23 Dec 2021 QA | Arithmetic - Time, Speed & Distance

During a marriage ceremony in Panipat, two shots from the air rifle are fired from the sameplace at an interval of 10 minutes 42 seconds. A man sitting in the train which is approaching the placewhere the ceremony is being held, hears the second sound after 10 minutes of hearing the first one.Assuming speed of sound to be 330 m/s, what could be the speed of the train?

A.
20.1 m/s
B.
12.4 m/s
C.
23.1 m/s
D.
30.1 m/s

10. IIFT 23 Dec 2021 QA | Geometry - Basics

If area of the adjacent faces of a cuboid is given as p, q and r respectively and the volume isgiven as 'V' then the square of the volume will be

A.
pqr
B.
$\frac{q r}{p^{2}}$
C.
$\frac{{(p q)}^{2}}{r^{2}}$
D.
(pqr)²

11. IIFT 23 Dec 2021 QA | Arithmetic - Simple & Compound Interest

If a principal P amounts to A in two years when compounded half yearly with r% interest. The same principal P amounts to A in two years when compounded annually with R% interest, then which of the following relationship is true?

A.
r > R
B.
r = R
C.
r < R
D.
r ≤ R

12. IIFT 23 Dec 2021 QA | Modern Math - Probability

In the galaxy “Andromeda”, a planet named “Exo” has a city called “Azith”. The city has analphabet system that consists of 48 letters and an octo-decimal number system (base -18). Theregistration number on the number plate of a vehicle in the city has two parts. The first part is the alphabetpart that consists of three letters and the second part is the number part that consists of 3 digits. The cityadministration issues all kinds of registration numbers with following restrictions:
a. The letters in the alphabet part are in ascending order and all letters must be distinct.
b. In the number part, the first digit is three more than the third digit.
Find the number of possible registration numbers available in the Azith city.

A.
3353270
B.
257830
C.
5339840
D.
4669920

13. IIFT 23 Dec 2021 QA | Geometry - Circles

The radius of circle is increased in a way such that its circumference increases by 8%. By howmuch percentage the area of the circle increases?

A.
12.5%
B.
16.64%
C.
10.5%
D.
6.4%

14. IIFT 23 Dec 2021 QA | Arithmetic - Ratio, Proportion & Variation

A group of 78 people watch NDTV, Times Now and Republic. Out of these news channels, 36 watch NDTV, 48 watch Times Now and 32 watches Republic. 14 people watch both NDTV and Times Now,20 people watch both Times Now and Republic, and 12 people watch both Republic and NDTV. Find the ratioof the number of people who watch only Times Now to the number of people who watch only Republic.

A.
9 : 4
B.
13 : 21
C.
11 : 4
D.
17 : 4

15. IIFT 23 Dec 2021 QA | Algebra - Simple Equations

Find the set S that denotes the set of all values of 'α' for which the roots of the equation (1 - α)x² - 6αx + 8α = 0 is greater than 2.

A.
$(\frac{2}{5}, \frac{1}{2})$
B.
$(\frac{2}{5}, \frac{32}{68})$
C.
$(\frac{32}{68}, 1)$
D.
$(\frac{32}{68}, \frac{1}{2})$

Answer: Option D

Explanation :

αf(x) = (1 - α)x² - 6αx + 8α = 0

Now roots are greater than 2 therefore,

$- \frac{b}{2 a}$ > 2

f(2) > 0

D > 0

$- \frac{b}{2 a}$ > 0

2(1 - α) > 0

$\frac{α}{α - 1}$ < 0

α ∈ (0, 1)

f(2) > 0

(1 − α ) 4 − 12α + 8α > 0
4 − 8α > 0

a < $\frac{1}{2}$

D > 0

36α² - 32α (1 - α) > 0

68α² - 32α > 0

α(68α - 32) > 0

α ∈ (-∞, 0) ∪ $(\frac{32}{68}, \infty)$

Taking the intersection of all we get α ∈ $(\frac{32}{68}, \frac{1}{2})$

16. IIFT 23 Dec 2021 QA | Geometry - Trigonometry

Evaluate:

[cos² $(\frac{π}{32})$ + cos² $(\frac{3 π}{32})$ + cos² $(\frac{5 π}{32})$ + ... + cos² $(\frac{15 π}{32})$ ] - [sin² $(\frac{π}{16})$ + sin² $(\frac{2 π}{16})$ + ... + sin² $(\frac{7 π}{16})$ ]

A.
1
B.
$\frac{1}{2}$
C.
$\frac{1}{3}$
D.
2

Answer: Option B

Explanation :

cos (A) = sin $(\frac{π}{2} - A)$

sin A = cos $(\frac{π}{2} - A)$

cos $(\frac{π}{32})$ = sin $(\frac{π}{2} - \frac{π}{32})$ = sin $(\frac{15 π}{32})$

sin² (A) + cos² (A) = 1

So the series simplifies to (1 + 1 + 1 + 1) - (1 + 1 + 1 + 1/2)
therefore value of series is 1/2

17. IIFT 23 Dec 2021 QA | Arithmetic - Profit & Loss

Same item is sold for Rs. 600 and Rs. 175, respectively. The profit earned on the first sale is 20times the loss incurred on the second sale. To make an overall profit of 30% in the whole transaction, atwhat price the second sale should happen:

A.
Rs. 310 approx
B.
Rs. 238 approx
C.
Rs. 254 approx
D.
Rs. 357 approx

18. IIFT 23 Dec 2021 QA | Modern Math - Probability

An unbiased dice is tossed seven times. Find the probability of getting a third six on the seventh throw.

A.
$\frac{(^{6} C_{3} \times 5^{3})}{6^{7}}$
B.
$\frac{(^{6} C_{2} \times 5^{4})}{6^{7}}$
C.
$\frac{(^{6} C_{3} \times 5^{3})}{6^{7}}$
D.
$\frac{(^{7} C_{3} \times 5^{4})}{6^{7}}$

Answer: Option B

Explanation :

We need a third 6 in the 7th throw which means that in the first 6 throws we should get 6 exactly twice.
No. of ways of getting 6 exactly twice in first 6 throws = ⁶C₂

Probability of getting 6 for the third time in the seventh throw = $\frac{(^{6} C_{2} \times 5^{4})}{6^{7}}$

19. IIFT 23 Dec 2021 QA | Geometry - Circles

There are 12 points in a two-dimensional plane with following coordinates: Points A, B, C, D, E,F, G have coordinates (1, 0), (2, 0), (3, 0), (4, 0), (5, 0), (6, 0) and (7, 0) respectively. Points H, I, J havecoordinates (1, 1), (2, 2) and (3, 3) respectively. Points K, L have coordinates (4, -2) and (5, -3)respectively. The number of circles possible with these points are?

A.
179
B.
158
C.
168
D.
147

20. IIFT 23 Dec 2021 QA | Algebra - Number System

“xyz” and “zyx” are three digit numbers where x, y, z are distinct digits from 0 to 9. Differenceof xyz and zyx has a factor of 7.

What is the maximum possible value of the LCM of x, y and z?

A.
126
B.
72
C.
90
D.
56

21. IIFT 23 Dec 2021 QA | Algebra - Logarithms

The value of x which satisfy 6 - 9 log₈ ${(\frac{4}{x})}^{\frac{1}{3}}$ - 8( ${(\log_{256} x)}^{\frac{2}{3}}$ - ${(\log_{2} x^{8})}^{\frac{1}{3}}$ = 0 is

A.
2
B.
$\sqrt{2}$
C.
4
D.
8

Answer: Option D

Explanation :

6 - 9 log₈ ${(\frac{4}{x})}^{\frac{1}{3}}$ - 8 ${(\log_{256} x)}^{\frac{2}{3}}$ - ${(\log_{2} x^{8})}^{\frac{1}{3}}$ = 0

6 - log₂ 4 + log₂ x - 2 ${(\log_{2} x)}^{\frac{2}{3}}$ - 2 ${(\log_{2} x)}^{\frac{1}{3}}$ = 0

Let ${(\log_{2} x)}^{\frac{1}{3}}$ be t.

4 + t³ - 2t² - 2t = 0

or, (t - 2) (t² - 2) = 0

so, t = 2 or

log₂ x = 8

22. IIFT 23 Dec 2021 QA | Geometry - Circles

Three small identical circles are inscribed inside an equilateral triangle with length 10 $\sqrt{3}$ cm as shown in the figure. The radius of each small circle is 2 cm A big circle touches these three circles as shown in the figure. Find the ratio of the area of the big circle with that of the area of the small circle. (figure not as per scale)

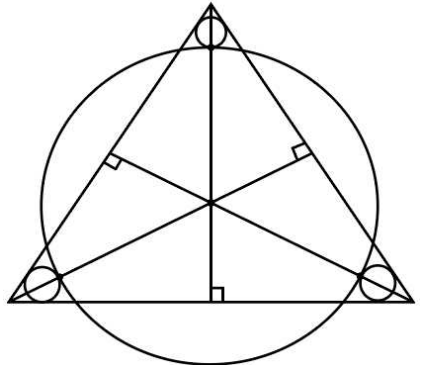
A.
4 : 1
B.
2 : 1
C.
3 : 1
D.
5 : 1

Answer: Option A

Explanation :

Height of triangle = (10 $\sqrt{3}$ ) × $(\frac{\sqrt{3}}{2})$ = 15
Distance between the centroid of the triangle and the vertex = 15 × $\frac{2}{3}$ = 10
Since in-radius is one-third of the height of the triangle
therefore, length of the line from vertex to the point where small circle and big circle touch each other = 10 - 6 = 4 cm
Radius of the bigger circle = 10 - 6 = 4 cm
Ratio of areas will be square of the ration of radius which is 4 : 1

23. IIFT 23 Dec 2021 QA | Arithmetic - Time, Speed & Distance

Abdul can go from his home to his favourite basketball ground by taking any of the two roads represented by y - x = 10 and 2x + 2y = 15. The ground is located at a distance of 200 units from each of the roads. What is the possible location of the basketball ground?

A.
(-1.25 + 200 $\sqrt{2}$ , 8.75)
B.
(-125 + $\frac{200}{\sqrt{2}}$ , 8.75 + $\frac{200}{\sqrt{2}}$ )
C.
(-1.25 + 100, 8.75 + 100 $\sqrt{3}$ )
D.
(-1.25 + 100 $\sqrt{3}$ , 8.75 + 100)

Answer: Option A

Explanation :

Distance of point (-1.25 + 200 $\sqrt{2}$ , 8.75) from lines y - x = 10 and x + y = 15/2

Distance from y - x = 10 is $|\frac{- 1.25 + 200 \sqrt{2} + 8.75 - 7.5}{\sqrt{1} + \sqrt{1}}|$ = 200

Distance from x + y = 15/2 is $\sqrt{1}$ + $\sqrt{1}$ = 200

24. IIFT 23 Dec 2021 QA | Arithmetic - Time, Speed & Distance

The rate at which coal is consumed by a RORO train, which is operated by Konkan Railways,fluctuates as the square of the speed. It is given that coal consumption of this train is 1200 kg/hour whenthe speed is 40 km/hour. Konkan Railway bears the cost of coal at the rate Rs. 16/100kg and all otherexpenses of running the RORO train costs Konkan Railways Rs. 13/hour. Find the total cost in paise/km, foroperating the RORO train when it is running at the speed of V km/hour.

A.
1300 + 5V²
B.
1300 + 12V²
C.
1300 + 75V²
D.
1300 + 16V²

Answer: Option B

Explanation :

Let rate of consumption per hour be R
Therefore, R = k(V²)
When speed = 40km/hr R = 1200 kg/hr
So, When speed = V
R = $(\frac{1200}{1600})$ × V²
Cost of coal consumed per hour = $(\frac{1200}{1600})$ × V² × $\frac{16}{100}$ = $\frac{12}{100}$ V²
All other expenses = Rs. 13/ hr
Therefore operating cost per hour = Rs. (13 + $\frac{12}{100}$ V²)
Operation cos in paise per hour = 1300 + 12V²

25. IIFT 23 Dec 2021 QA | Arithmetic - Ratio, Proportion & Variation

A can was full of olive oil. Lata draws each time 20% of the volume from the can and replaceswith groundnut oil. Usha draws 10% of the volume and replaces with mustard oil. Starting with Lata, bothrepeats the procedure alternatively two times each. What is the ratio of olive oil, groundnut oil and mustardoil in the end?

A.
7200 : 1800 : 1000
B.
5184 : 3096 : 1720
C.
5760 : 3440 : 800
D.
5436 : 3284 : 1280

Answer: Option B

Explanation :

Percentage of olive oil in the mixture = 100 × $(\frac{8}{10})$ × $(\frac{9}{10})$ × $(\frac{8}{10})$ × $(\frac{9}{10})$ = 51.84%

IIFT 23 Dec 2021 QA | Previous Year IIFT Paper

Feedback