LR - Mathematical Reasoning - Previous Year CAT/MBA Questions
The best way to prepare for LR - Mathematical Reasoning is by going through the previous year LR - Mathematical Reasoning CAT questions. Here we bring you all previous year LR - Mathematical Reasoning CAT questions along with detailed solutions.
Click here for previous year questions of other topics.
It would be best if you clear your concepts before you practice previous year LR - Mathematical Reasoning CAT questions.
Among the three, Neeta received the least amount in bank deposits, while Geeta received the highest. The value of the assets was distributed equally among the children, as were the gold coins. How many flats did Neeta receive?
Answer: 2
Text Explanation :
As per the data given in the question the gold coins were equally distributed amongst the 3 children. We are also told that the remaining assets (apart from the gold coins) are also equally distributed and that no flat or house is split or divided between 2 or more people. Only the bank deposit of Rs.70 lakhs can be split. Apart from the gold coins, the total value of the assets is 70 + 50 + 30 + 30 + 30 = 210 lakhs
So 210 lakhs split equally would means that each of the 3 daughters would get Rs.70 lakhs. This would mean that the person receiving the Rs.50 lakh house would get Rs.20 lakhs from the bank deposit. Now there are 3 flats of Rs.30 lakhs each and a balance of 50 lakhs in the bank deposit. The only way these assets can be split equally is if one of the 2 remaining people gets one of the flats of Rs.30 lakhs and receives 40 lakhs from the bank deposit. The second person would receive 70-40-20 = 10 Lakhs as bank deposit and 2 flats of 30 lakhs each, the sum of which adds upto 70 lakhs.
As Neeta receives the least amount in bank deposits, she will receive 10 lakhs. Also, as Geeta receives the highest amount in bank deposits she wil receive 40 lakhs.
Since Neeta is the person who receives the least amount in bank deposits i.e., 10 lakhs, he will receive 2 flats of 30 lakhs each.
Answer: 2
Workspace:
The value of the assets distributed among Neeta, Seeta and Geeta was in the ratio of 1 : 2 : 3, while the gold coins were distributed among them in the ratio of 2 : 3 : 4. One child got all three flats and she did not get the house. One child, other than Geeta, got Rs. 30 lakh in bank deposits.
How many gold coins did the old woman have?
- (a)
72
- (b)
90
- (c)
180
- (d)
216
Answer: Option B
Text Explanation :
As per the data given in the question the gold coins were equally distributed amongst the 3 children. We are also told that the remaining assets (apart from the gold coins) are also equally distributed and that no flat or house is split or divided between 2 or more people. Only the bank deposit of Rs.70 lakhs can be split. Apart from the gold coins, the total value of the assets is 70 + 50 + 30 + 30 + 30 = 210 lakhs
So 210 lakhs split equally would means that each of the 3 daughters would get Rs.70 lakhs. This would mean that the person receiving the Rs.50 lakh house would get Rs.20 lakhs from the bank deposit. Now there are 3 flats of Rs.30 lakhs each and a balance of 50 lakhs in the bank deposit. The only way these assets can be split equally is if one of the 2 remaining people gets one of the flats of Rs.30 lakhs and receives 40 lakhs from the bank deposit. The second person would receive 70-40-20 = 10 Lakhs as bank deposit and 2 flats of 30 lakhs each, the sum of which adds upto 70 lakhs.
As Neeta receives the least amount in bank deposits, she will receive 10 lakhs. Also, as Geeta receives the highest amount in bank deposits she wil receive 40 lakhs.
Let the total value of assets held by Neeta, Geeta and Seeta be x, 2x and 3x and the total number of gold coins held by each of them be 2y, 3y and 4y. So the total assets (apart from the gold coins) held by Neeta, Geeta and Seeta will be x – 2y, 2x – 3y and 3x – 4y.
Now total assets apart from gold coin = 210 lakhs
∴ (x – 2y) + (2x -3y) + (3x – 4y) = 210
⇒ 6x – 9y = 210
On simplifying we get 2x – 3y = 70
This means that the total assets held by Geeta apart from the gold coins = 70 lakhs We are further told that one child got all 3 flats and one person other than Geeta got 30 lakhs in bank deposits. So then the only way Geeta could have got assets (other than gold coins) worth 70 lakhs is by getting the house of 50 lakhs and 20 lakhs from the bank deposit. This is also because all the 3 flats of Rs. 30 lakh each have gone to one person and obviously that person cannot be Geeta. This means that the 3rd sister has got 20 lakhs from the bank deposit (since one more sister has got 30 lakhs). Since Geeta cannot receive 30 lakhs from the bank deposit, it would imply that Neeta will receive 30 lakhs and Geeta will receive 20 lakhs from the bank deposit.
Now, all 3 flats go to either Neeta or Geeta.
If all 3 flats are received by Neeta, then the ratio of value of assets of Neeta and Geeta
(in terms of y) will be (30 + 90 + 2y): (20 + 4y)
⇒ (120 + 2y) : (20 + 4y) =
⇒ 360 + 6y = 20 + 4y ⇒ 2y = -340 or y = -170
However ‘y’ cannot be a negative value. So all 3 flats will go to Geeta
∴ Ratio of value of assets of Neeta and Geeta (in terms of y) will be (30 + 2y) : (20 + 90 + 4y)
⇒ 90 + 6y = 110 + 4y ⇒ y = 10
Total number of gold coins = 2y + 3y + 4y = 9y = 90.
Hence, option (b).
Workspace:
The value of the assets distributed among Neeta, Seeta and Geeta was in the ratio of 1 : 2 : 3, while the gold coins were distributed among them in the ratio of 2 : 3 : 4. One child got all three flats and she did not get the house. One child, other than Geeta, got Rs. 30 lakh in bank deposits.
How much did Geeta get in bank deposits (in lakhs of rupees)?
Answer: 20
Text Explanation :
As per the data given in the question the gold coins were equally distributed amongst the 3 children. We are also told that the remaining assets (apart from the gold coins) are also equally distributed and that no flat or house is split or divided between 2 or more people. Only the bank deposit of Rs.70 lakhs can be split. Apart from the gold coins, the total value of the assets is 70 + 50 + 30 + 30 + 30 = 210 lakhs
So 210 lakhs split equally would means that each of the 3 daughters would get Rs.70 lakhs. This would mean that the person receiving the Rs.50 lakh house would get Rs.20 lakhs from the bank deposit. Now there are 3 flats of Rs.30 lakhs each and a balance of 50 lakhs in the bank deposit. The only way these assets can be split equally is if one of the 2 remaining people gets one of the flats of Rs.30 lakhs and receives 40 lakhs from the bank deposit. The second person would receive 70-40-20 = 10 Lakhs as bank deposit and 2 flats of 30 lakhs each, the sum of which adds upto 70 lakhs.
As Neeta receives the least amount in bank deposits, she will receive 10 lakhs. Also, as Geeta receives the highest amount in bank deposits she wil receive 40 lakhs.
Geeta gets 20 lakhs from bank deposits.
Answer: 20
Workspace:
Answer the following question based on the information given below.
Eight friends: Ajit, Byomkesh, Gargi, Jayanta, Kikira, Manik, Prodosh and Tapesh are goin to Delhi from Kolkatta by a flight operated by Cheap Air. In the flight, sitting is arranged in 30 rows, numbered 1 to 30, each consisting of 6 seats, marked by letters A to F from left to right, respectively. Seats A to C are to the left of the aisle (the passage running from the front of the aircraft to the back), and seats D to F are to the right of the aisle. Seats A and F are by the windows and referred to as Window seats, C and D are by the aisle and are referred to as Aisle seats while B and E are referred to as Middle seats. Seats marked by consecutive letters are called consecutive seats (or seats next to each other).A seat number is a combination of the row number, followed by the letter indicating the position in the row, e.g, 1A is the left window seat in the first row, while 12E is the right middle seat in the 12th row.
Cheap Air charges Rs. 1000 extra for any seats in Rows 1, 12 and 13 as those have extra legroom. For Rows 2-10, it charges Rs. 300 extra for Window seats and Rs. 500 extra for Aisle seats. For Rows 11 and 14 to 20, it charges Rs. 200 extra for Window seats and Rs. 400 extra for Aisle seats. All other seats are available at no extra charge.
The following are known:
- The eight friends were seated in six different rows.
- They occupied 3 Window seats, 4 Aisle seats and 1 Middle seat.
- Seven of them had to pay extra amounts, totaling to Rs. 4600, for their choices of seat. One of them did not pay any additional amount of his/her choice of seat.
- Jayanta, Ajit and Byomkesh were sitting in seats marked by the same letter, in consecutive rows in increasing order of row numbers; but all of them paid different amounts for their choices of seat. One of these amounts may be zero.
- Gargi was sitting next to Kikira, and Manik was sitting next to Jayanta.
- Prodosh and Tapesh were sitting in seats marked by the same letter, in consecutive rows in increasing order of row numbers; but they paid different amounts for their choices of seat. One of these amounts may be zero.
In which row was Manik sitting?
- (a)
10
- (b)
11
- (c)
12
- (d)
13
Answer: Option A
Text Explanation :
Using the information given in the questions let us tabulate the rates of the seats in the different rows.

Following condition (4) as Jayanta, Ajit and Byomkesh sit on seats marked by the same letter in increasing order of row in numbers and paid different amounts, the only way this would be possible is if they sat in rows 10, 11 and 12 respectively, either on the window seat or the aisle seat. So this would lead to 2 possible cases.
Case 1: Jayanta, Ajit and Byomkesh sit on the window seat in consecutive rows. In this case, as Manik sits adjacent to Jayanta, it would imply Manik sits on the middle seat next to Jayanta in row 10. This further implies that Manik did not pay any additional amount for his seat. Now Jayanta, Ajit and Byomkesh would pay an amount of 300 + 200 + 1000 = Rs. 1500. So the balance amount of 4600 – 1500 = 3100 must have been paid by Gargi, Kikira, Pradosh and Tapesh and all of them have to be occupying aisle seats. However, no contribution of amounts changeable for aisle seats adds upto 3100. So case is ruled out.
Case 2. Jayanta, Ajit and Byomkesh sit on the aisle seat in rows 10, 11 and 12 respectively. Here Manik can occupy either the middle seat next to Jayanta or the aisle seat next to Jayanta. Let us assume that Manik occupies the middle seat in row 10 next to Jayanta. In that case, cost of 3 aisle seats adds upto 4600 – (1000 + 500 + 400) = 2900. However, no contribution of amounts chargeable for the above mentioned seats adds upto 2900. So then Manik can only sit on the aisle seat adjacent to Jayanta in row 10. The total amount of seats chargeable to Jayanta, Ajit, Byomkesh and Manik adds upto 1000 + 500 + 400 + 500 = 2400. Now the balance amount of 4600 – 2400
= 2200 has to be accounted for by 4 people i.e., Gagi, Kikira, Pradosh and Tapesh. 3 of them sit on 3 window seats and one on the middle seat. Now out of Gargi and Kikira, one of them will sit on the middle seat and other on the window seat as they sit adjacent to each other. Which means that both Pradosh and Tapesh sit on the window seat. Since the amounts chargeable for the window/middle seats can only the amongst 1000, 300, 200 or 0 and the total we need to account for is 2200, at least one of the seats has to be a 1000 Rs. Seat. If we assume one of seats is Rs. 1000, then the balance amount of Rs 1200, cannot be accounted for. So there have to be at least 2 seats of Rs. 1000 each. Which means 2 out of Gargi, Kikira, Pradosh and Tapesh have to sit in the 13th row. Now these 2 people will have to be Gargi and Kikirsa as per condition (5). So each of Gargi and Kikira pay Rs. 1000 for their seat and these 2 seats will be a window and middle seat (both adjacent to each other)in the 13th row. The balance amount of Rs. 200 will be paid by Pradosh who sits on the window seat of the 20th row. This also implies that Tapesh will sit just behind Pradosh in the window seat of the 21st row. Let us represent all this information in the table given below

J – Jayanta, M – Manik, A – Ajit, B – Byomkesh, G – Gargi, K – Kikira, P – Pradosh, T – Tapesh
Using this data let us answer the question.
As can be seen from the table, Manik was sitting in row 10.
Hence, option (a).
Workspace:
How much extra did Jayanta pay for his choice of seat?
- (a)
Rs. 300
- (b)
Rs. 400
- (c)
Rs. 500
- (d)
Rs. 1000
Answer: Option C
Text Explanation :
Using the information given in the questions let us tabulate the rates of the seats in the different rows.

Following condition (4) as Jayanta, Ajit and Byomkesh sit on seats marked by the same letter in increasing order of row in numbers and paid different amounts, the only way this would be possible is if they sat in rows 10, 11 and 12 respectively, either on the window seat or the aisle seat. So this would lead to 2 possible cases.
Case 1: Jayanta, Ajit and Byomkesh sit on the window seat in consecutive rows. In this case, as Manik sits adjacent to Jayanta, it would imply Manik sits on the middle seat next to Jayanta in row 10. This further implies that Manik did not pay any additional amount for his seat. Now Jayanta, Ajit and Byomkesh would pay an amount of 300 + 200 + 1000 = Rs. 1500. So the balance amount of 4600 – 1500 = 3100 must have been paid by Gargi, Kikira, Pradosh and Tapesh and all of them have to be occupying aisle seats. However, no contribution of amounts changeable for aisle seats adds upto 3100. So case is ruled out.
Case 2. Jayanta, Ajit and Byomkesh sit on the aisle seat in rows 10, 11 and 12 respectively. Here Manik can occupy either the middle seat next to Jayanta or the aisle seat next to Jayanta. Let us assume that Manik occupies the middle seat in row 10 next to Jayanta. In that case, cost of 3 aisle seats adds upto 4600 – (1000 + 500 + 400) = 2900. However, no contribution of amounts chargeable for the above mentioned seats adds upto 2900. So then Manik can only sit on the aisle seat adjacent to Jayanta in row 10. The total amount of seats chargeable to Jayanta, Ajit, Byomkesh and Manik adds upto 1000 + 500 + 400 + 500 = 2400. Now the balance amount of 4600 – 2400
= 2200 has to be accounted for by 4 people i.e., Gagi, Kikira, Pradosh and Tapesh. 3 of them sit on 3 window seats and one on the middle seat. Now out of Gargi and Kikira, one of them will sit on the middle seat and other on the window seat as they sit adjacent to each other. Which means that both Pradosh and Tapesh sit on the window seat. Since the amounts chargeable for the window/middle seats can only the amongst 1000, 300, 200 or 0 and the total we need to account for is 2200, at least one of the seats has to be a 1000 Rs. Seat. If we assume one of seats is Rs. 1000, then the balance amount of Rs 1200, cannot be accounted for. So there have to be at least 2 seats of Rs. 1000 each. Which means 2 out of Gargi, Kikira, Pradosh and Tapesh have to sit in the 13th row. Now these 2 people will have to be Gargi and Kikirsa as per condition (5). So each of Gargi and Kikira pay Rs. 1000 for their seat and these 2 seats will be a window and middle seat (both adjacent to each other)in the 13th row. The balance amount of Rs. 200 will be paid by Pradosh who sits on the window seat of the 20th row. This also implies that Tapesh will sit just behind Pradosh in the window seat of the 21st row. Let us represent all this information in the table given below

J – Jayanta, M – Manik, A – Ajit, B – Byomkesh, G – Gargi, K – Kikira, P – Pradosh, T – Tapesh
Using this data let us answer the question.
Jayanta paid Rs.500 for his choice of seat.
Hence, option (c).
Workspace:
How much extra did Gargi pay for her choice of seat?
- (a)
0
- (b)
Rs. 300
- (c)
Rs. 400
- (d)
Rs. 1000
Answer: Option D
Text Explanation :
Using the information given in the questions let us tabulate the rates of the seats in the different rows.

Following condition (4) as Jayanta, Ajit and Byomkesh sit on seats marked by the same letter in increasing order of row in numbers and paid different amounts, the only way this would be possible is if they sat in rows 10, 11 and 12 respectively, either on the window seat or the aisle seat. So this would lead to 2 possible cases.
Case 1: Jayanta, Ajit and Byomkesh sit on the window seat in consecutive rows. In this case, as Manik sits adjacent to Jayanta, it would imply Manik sits on the middle seat next to Jayanta in row 10. This further implies that Manik did not pay any additional amount for his seat. Now Jayanta, Ajit and Byomkesh would pay an amount of 300 + 200 + 1000 = Rs. 1500. So the balance amount of 4600 – 1500 = 3100 must have been paid by Gargi, Kikira, Pradosh and Tapesh and all of them have to be occupying aisle seats. However, no contribution of amounts changeable for aisle seats adds upto 3100. So case is ruled out.
Case 2. Jayanta, Ajit and Byomkesh sit on the aisle seat in rows 10, 11 and 12 respectively. Here Manik can occupy either the middle seat next to Jayanta or the aisle seat next to Jayanta. Let us assume that Manik occupies the middle seat in row 10 next to Jayanta. In that case, cost of 3 aisle seats adds upto 4600 – (1000 + 500 + 400) = 2900. However, no contribution of amounts chargeable for the above mentioned seats adds upto 2900. So then Manik can only sit on the aisle seat adjacent to Jayanta in row 10. The total amount of seats chargeable to Jayanta, Ajit, Byomkesh and Manik adds upto 1000 + 500 + 400 + 500 = 2400. Now the balance amount of 4600 – 2400
= 2200 has to be accounted for by 4 people i.e., Gagi, Kikira, Pradosh and Tapesh. 3 of them sit on 3 window seats and one on the middle seat. Now out of Gargi and Kikira, one of them will sit on the middle seat and other on the window seat as they sit adjacent to each other. Which means that both Pradosh and Tapesh sit on the window seat. Since the amounts chargeable for the window/middle seats can only the amongst 1000, 300, 200 or 0 and the total we need to account for is 2200, at least one of the seats has to be a 1000 Rs. Seat. If we assume one of seats is Rs. 1000, then the balance amount of Rs 1200, cannot be accounted for. So there have to be at least 2 seats of Rs. 1000 each. Which means 2 out of Gargi, Kikira, Pradosh and Tapesh have to sit in the 13th row. Now these 2 people will have to be Gargi and Kikirsa as per condition (5). So each of Gargi and Kikira pay Rs. 1000 for their seat and these 2 seats will be a window and middle seat (both adjacent to each other)in the 13th row. The balance amount of Rs. 200 will be paid by Pradosh who sits on the window seat of the 20th row. This also implies that Tapesh will sit just behind Pradosh in the window seat of the 21st row. Let us represent all this information in the table given below

J – Jayanta, M – Manik, A – Ajit, B – Byomkesh, G – Gargi, K – Kikira, P – Pradosh, T – Tapesh
Using this data let us answer the question.
Gargi paid Rs.1000 extra for her choice of seat.
Hence, option (d).
Workspace:
Who among the following did not pay any extra amount for his/her choice of seat?
- (a)
Kikira
- (b)
Manik
- (c)
Gargi
- (d)
Tapesh
Answer: Option D
Text Explanation :
Using the information given in the questions let us tabulate the rates of the seats in the different rows.

Following condition (4) as Jayanta, Ajit and Byomkesh sit on seats marked by the same letter in increasing order of row in numbers and paid different amounts, the only way this would be possible is if they sat in rows 10, 11 and 12 respectively, either on the window seat or the aisle seat. So this would lead to 2 possible cases.
Case 1: Jayanta, Ajit and Byomkesh sit on the window seat in consecutive rows. In this case, as Manik sits adjacent to Jayanta, it would imply Manik sits on the middle seat next to Jayanta in row 10. This further implies that Manik did not pay any additional amount for his seat. Now Jayanta, Ajit and Byomkesh would pay an amount of 300 + 200 + 1000 = Rs. 1500. So the balance amount of 4600 – 1500 = 3100 must have been paid by Gargi, Kikira, Pradosh and Tapesh and all of them have to be occupying aisle seats. However, no contribution of amounts changeable for aisle seats adds upto 3100. So case is ruled out.
Case 2. Jayanta, Ajit and Byomkesh sit on the aisle seat in rows 10, 11 and 12 respectively. Here Manik can occupy either the middle seat next to Jayanta or the aisle seat next to Jayanta. Let us assume that Manik occupies the middle seat in row 10 next to Jayanta. In that case, cost of 3 aisle seats adds upto 4600 – (1000 + 500 + 400) = 2900. However, no contribution of amounts chargeable for the above mentioned seats adds upto 2900. So then Manik can only sit on the aisle seat adjacent to Jayanta in row 10. The total amount of seats chargeable to Jayanta, Ajit, Byomkesh and Manik adds upto 1000 + 500 + 400 + 500 = 2400. Now the balance amount of 4600 – 2400
= 2200 has to be accounted for by 4 people i.e., Gagi, Kikira, Pradosh and Tapesh. 3 of them sit on 3 window seats and one on the middle seat. Now out of Gargi and Kikira, one of them will sit on the middle seat and other on the window seat as they sit adjacent to each other. Which means that both Pradosh and Tapesh sit on the window seat. Since the amounts chargeable for the window/middle seats can only the amongst 1000, 300, 200 or 0 and the total we need to account for is 2200, at least one of the seats has to be a 1000 Rs. Seat. If we assume one of seats is Rs. 1000, then the balance amount of Rs 1200, cannot be accounted for. So there have to be at least 2 seats of Rs. 1000 each. Which means 2 out of Gargi, Kikira, Pradosh and Tapesh have to sit in the 13th row. Now these 2 people will have to be Gargi and Kikirsa as per condition (5). So each of Gargi and Kikira pay Rs. 1000 for their seat and these 2 seats will be a window and middle seat (both adjacent to each other)in the 13th row. The balance amount of Rs. 200 will be paid by Pradosh who sits on the window seat of the 20th row. This also implies that Tapesh will sit just behind Pradosh in the window seat of the 21st row. Let us represent all this information in the table given below

J – Jayanta, M – Manik, A – Ajit, B – Byomkesh, G – Gargi, K – Kikira, P – Pradosh, T – Tapesh
Using this data let us answer the question.
As Tapesh was sitting in row 21, he did not pay any extra amount for his seat.
Hence, option (d).
Workspace:
Answer the following question based on the information given below.
For admission to various affiliated colleges, a university conducts a written test with four different sections, each with a maximum of 50 marks. The following table gives the aggregate as well as the sectional cut-off marks fixed by six different colleges affiliated to the university. A student will get admission only if he/she gets marks greater than or equal to the cut-off marks in each of the sections and his/her aggregate marks are at least equal to the aggregate cut-off marks as specified by the college.
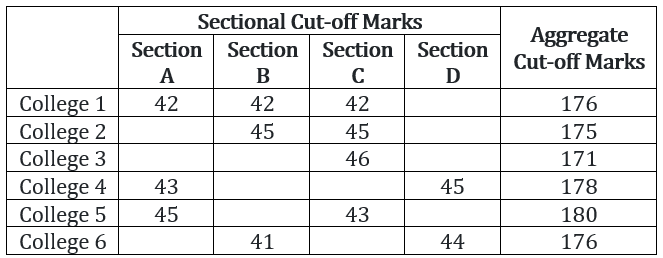
Aditya did not get a call from even a single college. What could be the maximum aggregate marks obtained by him?
- (a)
181
- (b)
176
- (c)
184
- (d)
196
- (e)
190
Answer: Option C
Text Explanation :
Since Aditya didn’t get a call from any of the colleges, so for each college, he either didn’t clear one of the sectional cut-offs or he didn’t clear the aggregate cut-off or both.
If he didn’t clear one of the sectional cut-offs, then for that section he scored less marks than the least cut-off among the given cut-offs of all the colleges.
For example, for section A, it is given that the cut-offs for colleges 1, 4 and 5 are 42, 43 and 45 respectively. The least cut-off among them is 42.
So, in order to not clear the sectional cut-off of section A for colleges 1, 4 and 5, he should have scored less than 42.
Similarly,
For colleges 1, 2 and 6, Aditya’s Section B marks < 41
For colleges 1, 2, 3 and 5, Aditya’s Section C marks < 42
For colleges 4 and 6, Aditya’s Section D marks < 44
If he scores less in Section C and D, he would not get calls for any colleges. Also in order to maximise the score we would assume that he got just one less than the cut-off in section C and D and he scored maximum marks (50) in other sections.
∴ Maximum marks obtained by Aditya such that he doesn’t get any calls = 41 + 43 + 50 + 50 = 184
Hence, option (c).
Workspace:
Bhama got calls from all colleges. What could be the minimum aggregate marks obtained by her?
- (a)
180
- (b)
181
- (c)
196
- (d)
176
- (e)
184
Answer: Option B
Text Explanation :
Since Bhama got calls from all colleges, she must have cleared each of the 4 sections. This means that for a particular section she scored more marks than the greatest cut-off for that section across the six colleges.
For example, for section A, it is given that the cut-offs for colleges 1, 4 and 5 are 42, 43 and 45 respectively. The greatest cut-off among them is 45.
So, in order to clear the sectional cut-off of section A for all the colleges, she should have scored at least 45.
Since we wish to minimise her marks, we should take her score in section A as 45.
Similarly, in sections B, C and D, she scored 45, 46, and 45 marks respectively.
∴ Bhama’s minimum marks such that she gets calls from all the colleges = 45 + 45 + 46 + 45 = 181
Hence, option (b).
Note: This is already greater than the highest aggregate cut-off of all colleges (which is 180 for college 5). So, she will get calls from all 6 colleges.
Workspace:
Charlie got calls from two colleges. What could be the minimum marks obtained by him in a section?
- (a)
0
- (b)
21
- (c)
25
- (d)
35
- (e)
41
Answer: Option C
Text Explanation :
The aggregate cut-off for each college is given in the common data. In order for Charlie to get minimum marks in one of the sections, he should have got maximum marks (i.e. 50) in the other three sections.
For example, the aggregate cut-off in college 1 is 176. Since, we want minimum marks in a section he should have gotten an aggregate of exactly 176. To minimise one of the sections, assume that he got 50 marks in the 3 sections whose cut-off is given in the common data. Then, Charlie will get a call from college 1 if he gets at least 176 – (50 × 3) = 26 marks in section D, provided that the cut-off for this section is also 26.
Now, there is at least one unknown sectional cut-off for each of the colleges, so we can use the same logic as used above for each of the remaining colleges.
For college 2, the minimum marks that Charlie needs to get a call = 175 – 150 = 25
For college 3, the minimum marks that Charlie needs to get a call = 171 – 150 = 21
For college 4, the minimum marks that Charlie needs to get a call = 178 – 150 = 28
For college 5, the minimum marks that Charlie needs to get a call = 180 – 150 = 30
For college 6, the minimum marks that Charlie needs to get a call = 176 – 150 = 26
The question states that Charlie only gets a call from 2 of the colleges. So, Charlie got 25 marks.
Hence, option (c).
Workspace:
Answer the following question based on the information given below.
There are 100 employees in an organization across five departments. The following table gives the departement-wise distribution of average age, average basic pay and allowances. The gross pay of an employee is the sum of his/her basic pay and allowances.
There are limited numbers of employees considered for transfer/promotion across departments. Whenever a person is transferred/promoted from a department of lower average age to a department of higher average age, he/she will get an additional allowance of 10% of basic pay over and above his/her current allowance. There will not be any change in pay structure if a person is transferred/promoted from a department with higher average age to a department with lower average age.
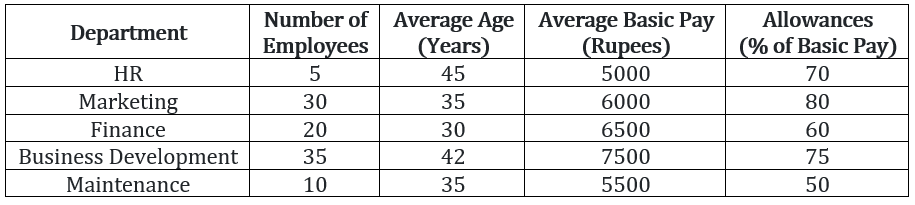
There was a mutual transfer of an employee between Marketing and Finance departments and transfer of one employee from Marketing to HR. As a result, the average age of Finance department increased by one year and that of Marketing department remained the same. What is the new average age of HR department?
- (a)
30
- (b)
35
- (c)
40
- (d)
45
- (e)
Cannot be determined
Answer: Option C
Text Explanation :
Let the age of the employee being transferred from the
1. Marketing department to the Finance department be x.
2. Finance department to the Marketing department be y.
3. Marketing department to the HR department be z.
Now,
The sum of the ages of all employees in Finance originally was 30 × 20 = 600. Later, an employee of x years of age joined the department and one of y years of age left it.
So, the new average age for the Finance department = = 31 (given)
∴ 600 + x – y = 620
∴ x – y = 20 … (i)
The sum of the ages of all employees in Marketing originally was 35 × 30 = 1050.
Later, two employees of x years and z years of age left the department and one of y years of age joined it. Since 2 employees left and 1 joined, hence the number of employees currently in this department is 29
So, the new average age for the Marketing department = . = 35 (given)
∴ 1050 – x + y – z = 1015
∴ x – y + z = 35 … (ii)
From equations (i) and (ii), we get,
20 + z = 35
∴ z = 15
The sum of the ages of all employees in HR originally was 45 × 5 = 225.
Later, one employee of z years of age joined the department. Also, the number of employees increases by one to 6.
So, the new average age for the HR department =
Hence, option (c).
Workspace:
What is the approximate percentage change in the average gross pay of the HR department due to transfer of a 40-yr old person with basic pay of Rs. 8000 from the Marketing department?
- (a)
9%
- (b)
11%
- (c)
13%
- (d)
15%
- (e)
17%
Answer: Option C
Text Explanation :
The average age of the Marketing department is 35 years and that of the HR department is 45 years. So, the employee is being transferred from a department with a lower average age to one with a higher average age, which means that he gets an additional allowance of 10% of basic pay over his current allowance.
His current allowance = 80% of 8000 = 6400
Therefore, his new allowance = 6400 + 10% of 8000 = 6400 + 800 = 7200
After the transfer, his gross pay = 8000 + 7200 = 15200
Initially, the average gross pay of the HR department = 5000 + 70% of 5000 = 8500
The new average gross pay of the HR department (i.e. after the transfer of the 40-yr old)
∴ The percentage change in the average gross pay of the HR department
× 100 ≈ 13.13%
Hence, option (c).
Workspace:
If two employees (each with a basic pay of Rs. 6000) are transferred from Maintenance department to HR department and one person (with a basic pay of Rs. 8000) was transferred from Marketing department to HR department, what will be the percentage change in average basic pay of HR department?
- (a)
10.5%
- (b)
12.5%
- (c)
15%
- (d)
30%
- (e)
40%
Answer: Option B
Text Explanation :
Note that in this question, the percentage change in basic pay is asked. According to the common data, only the allowances (and hence the gross pay) is affected when a person is transferred. The basic pay of a person remains unaltered.
∴ The average basic pay after the transfers have taken place
∴ The percentage change in the average basic pay of the HR department
× 100 = 12.5%
Hence, option (b).
Workspace:
Answer the following question based on the information given below.
Abdul, Bikram and Chetan are three professional traders who trade in shares of a company XYZ Ltd. Abdul follows the strategy of buying at the opening of the day at 10 am and selling the whole lot at the close of the day at 3 pm. Bikram follows the strategy of buying at hourly intervals: 10 am , 11 am, 12 noon, 1 pm and 2 pm, and selling the whole lot at the close of the day. Further, he buys an equal number of shares in each purchase. Chetan follows a similar pattern as Bikram but his strategy is somewhat different. Chetan’s total investment amount is divided equally among his purchases. The profit or loss made by each investor is the difference between the sale value at the close of the day less the investment in purchase. The “return” for each investor is defined as the ratio of the profit or loss to the investment amount expressed as a percentage.
On a “boom” day the price of XYZ Ltd. keeps rising throughout the day and peaks at the close of the day. Which trader got the minimum return on that day?
- (a)
Bikram
- (b)
Chetan
- (c)
Abdul
- (d)
Abdul or Chetan
- (e)
Cannot be determined
Answer: Option A
Text Explanation :
Firstly, let us try to understand the way the investments of the three traders behave.
Abdul buys shares at 10 am everyday and sells them at a particular price at 3 pm. So his return is determined by the difference in the share price at these two times.
Bikram and Chetan buy shares at equal intervals. But since Chetan buys them in equal amount he would end up buying more when the price is less and less when the price is more.
Whether the prices are continuously rising or continuously falling down or in a fluctuating market, Chetan always has a higher proportion of lower priced shares as compared to Bikram. This increases his profit in a rising market and reduces his loss in a falling market. Therefore Chetan never has return lower than that of Bikram.
We have explained this concept by taking examples. For more depth we have also provided the theoretical explanation. The theoretical explanation is only for better understanding and may not be suitable in a test environment.
Consider the scenario when the share price keeps rising throughout the day.
Let the share price at 10 am be Rs. 100, 11 am be Rs. 110, 12 noon be Rs. 140, 1 pm be Rs. 150, 2 pm be Rs. 180, and finally at 3 pm be Rs. 200.

Abdul buys shares at Rs. 100 at 10 am and sells them at Rs. 200 at 3 pm.
∴ Abdul’s return is 100%.
Let Bikram buy one share at each interval. So, at 10 am, he buys a share for Rs. 100; at 11 am, he buys a share for Rs. 110; at 12 noon, he buys a share for Rs. 140; at 1 pm, he buys a share for Rs. 150; and at 2 pm, he buys a share for 180 × 1 = Rs. 180.
Thus, he buys a total of 5 shares for 100 + 110 + 140 + 150 + 180 = Rs. 680
At 3 pm, he sells all 5 shares for 200 × 5 = Rs. 1,000. Thus, his profit will be 1,000 − 680 = Rs. 320
Hence, Bikram's return is × 100 ≈ 47%
Let Chetan invest Rs. 415,800 at each interval. So, at 10 am, he buys 415800/100 = 4158 shares; at 11 am, he buys 415800/110 = 3780 shares; at 12 noon, he buys 415800/140 = 2970 shares; at 1 pm, he buys 415800/150 = 2772 shares; at 2 pm, he buys 415800/180 = 2310 shares.
Thus, he buys 4158 + 3780 + 2970 + 2772 + 2310 = 15990 shares for 415800 × 5 = Rs. 20,79,000. He sells these shares for 200 × 15990 = Rs. 31,98,000. His profit will be 3198000 − 2079000 = Rs. 11,19,000.
Hence Chetan's returns = × 100 ≈ 53%
From the above example, we see that in case of continuously rising share prices,
Abdul’s return > Chetan’s return > Bikram’s return
Thus Bikram gets the minimum return on a “boom” day.
Hence, option (a).
Note: Theoretical Explanation:
Let x1, x2, … , x6 be the share prices at 10 am, 11 am, 12 noon, 1 pm, 2 pm and 3 pm respectively.
For Abdul:
Abdul buys shares at Rs. x1 and sells them at Rs. x6.
∴ Abdul's returns =
For Bikram:
Let Bikram have bought n shares at each hourly interval.
His investment amount = nx1 + nx2 + nx3 + nx4 + nx5
= n(x1 + x2 + x3 + x4 + x5)
At 3 pm, he sells his shares for (5n × x6)
Hence, his profit/loss = (n × 5x6) - n ×
= n ×
∴ Bikram's returns =
Hence, Bikram's returns =
For Chetan:
Let Chetan invest Rs. P at each hourly interval.
His investment amount = 5P
Since he invests Rs. P at each interval, he buys shares at 10 am; at 11 am; and so on until 2 pm.
At 3 pm, he sells each share at x6. So, for all his shares, he receives,
Rs.
= Px6 ×
Hence, his profit/loss = Px6 × - 5P
= P ×
∴ Chetan's returns =
∴ Chetan's returns =
Now, let’s compare Bikram’s and Chetan’s returns. Since Arithmetic Mean is always greater than or equal to the Harmonic Mean, Chetan’s returns will be greater than or equal to Bikram’s.
Workspace:
On a day of fluctuating market prices, the share price of XYZ Ltd. ends with a gain, i.e., it is higher at the close of the day compared to the opening value. Which trader got the maximum return on that day?
- (a)
Bikram
- (b)
Chetan
- (c)
Abdul
- (d)
Bikram or Chetan
- (e)
Cannot be determined
Answer: Option E
Text Explanation :
Since Chetan’s return is always higher than or equal to that of Bikram, the trader with the maximum return would be either Abdul or Chetan.
If it is a continuously rising market then Abdul would end up having the highest gain as seen in the example above.
But there might be a scenario when the share price of XYZ would go down after 10 AM and rise in the end at 3 PM to a higher value.
In such a case, if Chetan gets the shares at lower prices than what the price was at 10 AM he would end up making more profit and hence higher return.

Here, Abdul’s returns remain unaltered as 100%.
Let Chetan always buy shares worth Rs. 100.
So he would end up buying 1 + 10 + 10 + 10 + 10 = 41 shares.
When he sells the same at Rs. 200 he gets Rs. 8,200 for the same.
∴ Chetan’s profit = 8200 − 500 = 7700
∴ Chetan's returns =
∴ We cannot say for sure who would have higher returns.
Hence, option (e).
Workspace:
Which one of the following statements is always true?
- (a)
Abdul will not be the one with the minimum return
- (b)
Return for Chetan will be higher than that of Bikram
- (c)
Return for Bikram will be higher than that of Chetan
- (d)
Return for Chetan cannot be higher than that of Abdul
- (e)
none of the above
Answer: Option E
Text Explanation :
From the explanation seen till now we can rule out options 1, 3 and 4.
Now option 2 is only partially correct. We have seen that Chetan’s return would be higher than or equal to that of Bikram. It would be equal to Bikram’s return in the scenario when the share price remains at a constant value throughout the day.
∴ Option 2 is not always true.
Hence, option (e).
Workspace:
One day, two other traders, Dane and Emily joined Abdul, Bikram and Chetan for trading in the shares of XYZ Ltd. Dane followed a strategy of buying equal numbers of shares at 10 am, 11 am and 12 noon, and selling the same numbers at 1 pm, 2 pm and 3 pm. Emily, on the other hand, followed the strategy of buying shares using all her money at 10 am and selling all of them at 12 noon and again buying the shares for all the money at 1 pm and again selling all of them at the close of the day at 3 pm. At the close of the day the following was observed:
i. Abdul lost money in the transactions.
ii. Both Dane and Emily made profits.
iii. There was an increase in share price during the closing hour compared to the price at 2 pm.
iv. Share price at 12 noon was lower than the opening price.
Which of the following is necessarily false?
- (a)
Share price was at its lowest at 2 pm
- (b)
Share price was at its lowest at 11 am
- (c)
Share price at 1 pm was higher than the share price at 2 pm
- (d)
Share price at 1 pm was higher than the share price at 12 noon
- (e)
None of the above
Answer: Option A
Text Explanation :
Let x1, x2, … , x6 be the share prices at 10 am, 11 am, 12 noon, 1 pm, 2 pm and 3 pm respectively.
Now, since Abdul lost money in the transaction,
x1 > x6
Combining the above, we have,
x1 > x6 > x5
and x1 > x3,
Also, let the money Emily invests at 10 am be Rs. P. Then,
Her investment = Rs. P
And the number of shares she buys = P/x1
So, after selling these shares at 12 noon, she will get Rs. (P/x1) × x3
Now, she invests the money at 1 pm, and the number of shares she buys =
So, after selling these shares at 3 pm, she gets Rs.
So, her returns =
Since she made profit, her returns > 0;
i.e. or
Now, we know that x1 > x6; so cannot be > 1.
has to be > 1; i.e. x3 > x4
∴ The share price at 12 noon is greater than that at 1 pm.
Hence, option (d) is definitely false.
Also, since in the first half, Emily invests at 10 am and sells at 12 noon, and we know that the share price at 10 am was greater than at 12 noon; hence she must have suffered a loss during this transaction. However, she makes a net profit in the end. So, she must have made profit during the second part of the transaction; i.e. the share price at 1 pm must have been less than that at 3 pm.
i.e. x4 < x6,
Also, let Dane buy n shares at 10 am, 11 am and 12 noon.
Hence, her investment = n(x1 + x2 + x3)
And she sells these at 1 pm, 2 pm and 3 pm for n(x4 + x5 + x6)
∴ her returns =
Since she made profit, her returns are greater than 0;
i.e. or
Hence, (x4+ x5+x6 )> (x1+ x2+x3 )
Since, x1 > x6 and x3 > x4, hence x5 > x2
So far, we have,
x1 > x6 > x5 > x2, x4 < x6 and x1 > x3 > x4
Now from Dane’s investment, we know that,
(x4+ x5+ x6) - (x1+ x2+x3 ) > 0 … (i)
Keeping in mind the relationships between the share prices, we have
x6 = x1 – b
x4 = x1 – b – c
x3 = x1 – b – c + a
x5 = x1 – d, where a, b, c and d are all positive.
Substituting the above in equation (i), we have,
(x1 – b – c + x1 – d + x1 – b) – (x1 + x2 + x1 – b – c + a) > 0
∴ x1 - x2 > b + d + a (which is > 0, since all the variables are positive)
i.e. x1 > x2
∴ x2 < x1 – b – a – d
∴ x2 is definitely less than x6 and x5.
∴ Although we don’t know when the share price is at its lowest, we do know that x5 > x2.
∴ x5, i.e. the share price at 2 pm is not the lowest.
Hence, option (a) is also definitely false.
Thus there are two options which are correct for this question. This is an ambiguity and therefore, we are not indicating any option as correct.
Workspace:
Share price was at its highest at
Note: Use data from the previous question.
- (a)
10 am
- (b)
11 am
- (c)
12 noon
- (d)
1 pm
- (e)
Cannot be determined
Answer: Option A
Text Explanation :
From the solution of the last question, we can see that,
x1 > x6 > x5 > x2, x4 < x6 and x1 > x3 > x4
∴ x1, i.e. the share price at 10 is the highest.
Hence, option (a).
Workspace:
Answer the following question based on the information given below.
Mathematicians are assigned a number called Erdös number, (named after the famous mathematician, Paul Erdös). Only Paul Erdös himself has an Erdös number of zero. Any mathematician who has written a research paper with Erdös has an Erdös number of 1. For other mathematicians, the calculation of his/her Erdös number is illustrated below:
Suppose that a mathematician X has co-authored papers with several other mathematicians. From among them, mathematician Y has the smallest Erdös number. Let the Erdös number of Y be y. Then X has an Erdös number of y + 1. Hence any mathematician with no co-authorship chain connected to Erdös has an Erdös number of infinity.
- In a seven day long mini-conference organized in memory of Paul Erdös, a close group of eight mathematicians, call them A, B, C, D, E, F, G and H, discussed some research problems. At the beginning of the conference, A was the only participant who had an infinite Erdös number. Nobody had an Erdös number less than that of F.
- On the third day of the conference F co-authored a paper jointly with A and C. This reduced the average Erdös number of the group of eight mathematicians to 3. The Erdös numbers of B, D, E, G and H remained unchanged with the writing of this paper. Further, no other co-authorship among any three members would have reduced the average Erdös number of the group of eight to as low as 3.
- At the end of the third day, five members of this group had identical Erdös numbers while the other three had Erdös numbers distinct from each other.
- On the fifth day, E co-authored a paper with F which reduced the group‘s average Erdös number by 0.5. The Erdös numbers of the remaining six were unchanged with the writing of this paper.
- No other paper was written during the conference.
The person having the largest Erdös number at the end of the conference must have had Erdös number (at that time):
- (a)
5
- (b)
7
- (c)
9
- (d)
14
- (e)
15
Answer: Option B
Text Explanation :
Let F and E have Erdös numbers f and e respectively at the beginning of the conference.
On the third day, A’s and C’s Erdös numbers become (f + 1)
The sum of Erdös numbers changed to 8 × 3 = 24
At the end of the third day, five members had identical Erdös numbers while the other three had distinct ones.
On the fifth day, E’s Erdös numbers became f + 1 and this reduced the group’s average by 0.5. This means that E’s Erdös numbers was not f + 1 on the third day.
Thus we have,
At the end of the third day, 5(f + 1) + f + e + y = 24
Hence 6f + 5 + e + y = 24
Hence 6f + e + y = 19
At the end of the fifth day,
6(f + 1) + f + y = 2.5 × 8 = 20
Hence 7f + y = 14
Among the eight mathematicians, F has the smallest Erdös number.
Let f = 2
∴ y = 0
However, only Paul Erdös himself has an Erdös number of 0. So f cannot be equal to 2. Any other value greater than 2, would render y as a negative number, which is also not possible.
So, f = 1
∴ y = 7
∴ e = 6
Now, we can solve all the questions.
From the above explanation, the largest Erdös number at the end of the conference would be 7.
Hence, option (b).
Workspace:
How many participants in the conference did not change their Erdös number during the conference?
- (a)
2
- (b)
3
- (c)
4
- (d)
5
- (e)
Cannot be determined
Answer: Option D
Text Explanation :
Let F and E have Erdös numbers f and e respectively at the beginning of the conference.
On the third day, A’s and C’s Erdös numbers become (f + 1)
The sum of Erdös numbers changed to 8 × 3 = 24
At the end of the third day, five members had identical Erdös numbers while the other three had distinct ones.
On the fifth day, E’s Erdös numbers became f + 1 and this reduced the group’s average by 0.5. This means that E’s Erdös numbers was not f + 1 on the third day.
Thus we have,
At the end of the third day, 5(f + 1) + f + e + y = 24
Hence 6f + 5 + e + y = 24
Hence 6f + e + y = 19
At the end of the fifth day,
6(f + 1) + f + y = 2.5 × 8 = 20
Hence 7f + y = 14
Among the eight mathematicians, F has the smallest Erdös number.
Let f = 2
∴ y = 0
However, only Paul Erdös himself has an Erdös number of 0. So f cannot be equal to 2. Any other value greater than 2, would render y as a negative number, which is also not possible.
So, f = 1
∴ y = 7
∴ e = 6
Now, we can solve all the questions.
From the above explanation, the Erdös numbers of B, D, G, H and F did not change during the conference.
Hence, option (d).
Workspace:
The Erdös number of C at the end of the conference was:
- (a)
1
- (b)
2
- (c)
3
- (d)
4
- (e)
5
Answer: Option B
Text Explanation :
Let F and E have Erdös numbers f and e respectively at the beginning of the conference.
On the third day, A’s and C’s Erdös numbers become (f + 1)
The sum of Erdös numbers changed to 8 × 3 = 24
At the end of the third day, five members had identical Erdös numbers while the other three had distinct ones.
On the fifth day, E’s Erdös numbers became f + 1 and this reduced the group’s average by 0.5. This means that E’s Erdös numbers was not f + 1 on the third day.
Thus we have,
At the end of the third day, 5(f + 1) + f + e + y = 24
Hence 6f + 5 + e + y = 24
Hence 6f + e + y = 19
At the end of the fifth day,
6(f + 1) + f + y = 2.5 × 8 = 20
Hence 7f + y = 14
Among the eight mathematicians, F has the smallest Erdös number.
Let f = 2
∴ y = 0
However, only Paul Erdös himself has an Erdös number of 0. So f cannot be equal to 2. Any other value greater than 2, would render y as a negative number, which is also not possible.
So, f = 1
∴ y = 7
∴ e = 6
Now, we can solve all the questions.
From the above explanation, C’s Erdös number was f + 1 = 2 on the third day and thereafter.
Hence, option (b).
Workspace:
The Erdös number of E at the beginning of the conference was:
- (a)
2
- (b)
5
- (c)
6
- (d)
7
- (e)
8
Answer: Option C
Text Explanation :
Let F and E have Erdös numbers f and e respectively at the beginning of the conference.
On the third day, A’s and C’s Erdös numbers become (f + 1)
The sum of Erdös numbers changed to 8 × 3 = 24
At the end of the third day, five members had identical Erdös numbers while the other three had distinct ones.
On the fifth day, E’s Erdös numbers became f + 1 and this reduced the group’s average by 0.5. This means that E’s Erdös numbers was not f + 1 on the third day.
Thus we have,
At the end of the third day, 5(f + 1) + f + e + y = 24
Hence 6f + 5 + e + y = 24
Hence 6f + e + y = 19
At the end of the fifth day,
6(f + 1) + f + y = 2.5 × 8 = 20
Hence 7f + y = 14
Among the eight mathematicians, F has the smallest Erdös number.
Let f = 2
∴ y = 0
However, only Paul Erdös himself has an Erdös number of 0. So f cannot be equal to 2. Any other value greater than 2, would render y as a negative number, which is also not possible.
So, f = 1
∴ y = 7
∴ e = 6
Now, we can solve all the questions.
From the above explanation, E’s Erdös number was 6.
Hence, option (c).
Workspace:
How many participants had the same Erdös number at the beginning of the conference?
- (a)
2
- (b)
3
- (c)
4
- (d)
5
- (e)
Cannort be determined
Answer: Option B
Text Explanation :
Since 5 participants had identical Erdös numbers at the end of day three and two of these were A and C whose Erdös numbers had changed on the same day, three had the same Erdös numbers at the beginning of the conference.
Hence, option (b).
Workspace:
Answer the following question based on the information given below.
Two traders, Chetan and Michael, were involved in the buying and selling of MCS shares over five trading days. At the beginning of the first day, the MCS share was priced at Rs. 100, while at the end of the fifth day it was priced at Rs. 110. At the end of each day, the MCS share price either went up by Rs. 10, or else, it came down by Rs. 10. Both Chetan and Michael took buying and selling decisions at the end of each trading day.
The beginning price of MCS share on a given day was the same as the ending price of the previous day.
Chetan and Michael started with the same number of shares and amount of cash, and had enough of both. Below are some additional facts about how Chetan and Michael traded over the five trading days.
- Each day if the price went up, Chetan sold 10 shares of MCS at the closing price. On the other hand, each day if the price went down, he bought 10 shares at the closing price.
- If on any day, the closing price was above Rs. 110, then Michael sold 10 shares of MCS, while if it was below Rs. 90, he bought 10 shares, all at the closing price.
If Chetan sold 10 shares of MCS on three consecutive days, while Michael sold 10 shares only once during the five days, what was the price of MCS at the end of day 3?
- (a)
Rs. 90
- (b)
Rs. 100
- (c)
Rs. 110
- (d)
Rs. 120
- (e)
Rs. 130
Answer: Option C
Text Explanation :
Let the price of the share rise on x days and fall on y days. As the price increases by Rs. 10 in the five days, we have:
x + y = 5 and 10x – 10y = 10
Solving the above two equations simultaneously, we have
x = 3 and y = 2
The price of the share goes up on 3 days and falls on 2 days.
The three days on which the price rises can be selected in 5C3 = 10 ways
The following are the 10 cases:

Consider Case 5:
Chetan sells on Days 1, 2 and 4 and buys on days 3 and 5.
Change in the number of shares he has = –30 + 20 = –10
Change in his cash = 10 × (110 + 120 + 120) – 10 × (110 + 110) = Rs. 1300
Michael sells on days 2 and 4, but never buys as the share price does not go below Rs. 90.
Change in the number of shares he has = –20
Change in his cash = 10 × (120 + 120) = Rs. 2400
The other cases are evaluated in a similar manner and the data is tabulated as shown above.
Chetan sold on three consecutive days: Cases 1, 2 and 3.
Michael sold only once: Case 3.
∴ The price of the share at the end of day 3 = Rs. 110
Hence, option (c).
Workspace:
If Michael ended up with Rs. 100 less cash than Chetan at the end of day 5, what was the difference in the number of shares possessed by Michael and Chetan (at the end of day 5)?
- (a)
Michael had 10 less shares than Chetan.
- (b)
Michael had10 more shares than Chetan.
- (c)
Chetan had 10 more shares than Michael.
- (d)
Chetan had 20 more shares than Michael.
- (e)
Both had the same number of shares.
Answer: Option E
Text Explanation :
Let the price of the share rise on x days and fall on y days. As the price increases by Rs. 10 in the five days, we have:
x + y = 5 and 10x – 10y = 10
Solving the above two equations simultaneously, we have
x = 3 and y = 2
The price of the share goes up on 3 days and falls on 2 days.
The three days on which the price rises can be selected in 5C3 = 10 ways
The following are the 10 cases:

Consider Case 5:
Chetan sells on Days 1, 2 and 4 and buys on days 3 and 5.
Change in the number of shares he has = –30 + 20 = –10
Change in his cash = 10 × (110 + 120 + 120) – 10 × (110 + 110) = Rs. 1300
Michael sells on days 2 and 4, but never buys as the share price does not go below Rs. 90.
Change in the number of shares he has = –20
Change in his cash = 10 × (120 + 120) = Rs. 2400
The other cases are evaluated in a similar manner and the data is tabulated as shown above.
Chetan sold on three consecutive days: Cases 1, 2 and 3.
Michael sold only once: Case 3.
Michael ends up with Rs. 100 less cash than Chetan in cases 3, 6 and 8. In each of these cases, both of them hold the same number of shares at the end of day 5.
Hence, option (e).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report