LR - Mathematical Reasoning - Previous Year CAT/MBA Questions
The best way to prepare for LR - Mathematical Reasoning is by going through the previous year LR - Mathematical Reasoning CAT questions. Here we bring you all previous year LR - Mathematical Reasoning CAT questions along with detailed solutions.
Click here for previous year questions of other topics.
It would be best if you clear your concepts before you practice previous year LR - Mathematical Reasoning CAT questions.
Answer the following questions based on the information given below.
Six web surfers M, N, O, P, X, and Y each had 30 stars which they distributed among four bloggers A, B, C, and D. The number of stars received by A and B from the six web surfers is shown in the figure below.

The following additional facts are known regarding the number of stars received by the
bloggers from the surfers.
1. The numbers of stars received by the bloggers from the surfers were all multiples of 5
(including 0).
2. The total numbers of stars received by the bloggers were the same.
3. Each blogger received a different number of stars from M.
4. Two surfers gave all their stars to a single blogger.
5. D received more stars than C from Y
What was the total number of stars received by D?
Answer: 45
Text Explanation :
Workspace:
What was the number of stars received by D from Y?
- (a)
10
- (b)
0
- (c)
5
- (d)
Cannot be determined
Answer: Option C
Text Explanation :
Workspace:
How many surfers distributed their stars among exactly 2 bloggers?
Answer: 2
Text Explanation :
Workspace:
Which of the following can be determined with certainty?
I. The number of stars received by C from M
II. The number of stars received by D from O
- (a)
Only I
- (b)
Neither I nor II
- (c)
Both I and II
- (d)
Only II
Answer: Option A
Text Explanation :
Workspace:
Answer the following questions based on the information given below.
Two students, Amiya and Ramya are the only candidates in an election for the position of class representative. Students will vote based on the intensity level of Amiya’s and Ramya’s campaigns and the type of campaigns they run. Each campaign is said to have a level of 1 if it is a staid campaign and a level of 2 if it is a vigorous campaign. Campaigns can be of two types, they can either focus on issues, or on attacking the other candidate.
If Amiya and Ramya both run campaigns focusing on issues, then
- The percentage of students voting in the election will be 20 times the sum of the levels of campaigning of the two students. For example, if Amiya and Ramya both run vigorous campaigns, then 20 × (2+2)%, that is, 80% of the students will vote in the election.
- Among voting students, the percentage of votes for each candidate will be proportional to the levels of their campaigns. For example, if Amiya runs a staid (i.e., level 1) campaign while Ramya runs a vigorous (i.e., level 2) campaign, then Amiya will receive 1/3 of the votes cast, and Ramya will receive the other 2/3. The above-mentioned percentages change as follows if at least one of them runs a campaign attacking their opponent.
- If Amiya runs a campaign attacking Ramya and Ramya runs a campaign focusing on issues, then 10% of the students who would have otherwise voted for Amiya will vote for Ramya, and another 10% who would have otherwise voted for Amiya, will not vote at all.
- If Ramya runs a campaign attacking Amiya and Amiya runs a campaign focusing on issues, then 20% of the students who would have otherwise voted for Ramya will vote for Amiya, and another 5% who would have otherwise voted for Ramya, will not vote at all.
- If both run campaigns attacking each other, then 10% of the students who would have otherwise voted for them had they run campaigns focusing on issues, will not vote at all.
If both of them run staid campaigns attacking the other, then what percentage of students will vote in the election?
- (a)
60%
- (b)
36%
- (c)
64%
- (d)
40%
Answer: Option B
Text Explanation :
Workspace:
What is the minimum percentage of students who will vote in the election?
- (a)
40%
- (b)
32%
- (c)
38%
- (d)
36%
Answer: Option D
Text Explanation :
Workspace:
If Amiya runs a campaign focusing on issues, then what is the maximum percentage of votes that she can get?
- (a)
48%
- (b)
40%
- (c)
44%
- (d)
36%
Answer: Option A
Text Explanation :
Workspace:
If Ramya runs a campaign attacking Amiya, then what is the minimum percentage of votes that she is guaranteed to get?
- (a)
12%
- (b)
18%
- (c)
15%
- (d)
30%
Answer: Option C
Text Explanation :
Workspace:
Answer the following questions based on the information given below.
The numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are placed in ten slots of the following grid based on the conditions below.
1. Numbers in any row appear in an increasing order from left to right.
2. Numbers in any column appear in a decreasing order from top to bottom.
3. 1 is placed either in the same row or in the same column as 10.
4. Neither 2 nor 3 is placed in the same row or in the same column as 10.
5. Neither 7 nor 8 is placed in the same row or in the same column as 9.
6. 4 and 6 are placed in the same row.
What is the row number which has the least sum of numbers placed in that row?
Answer: 4
Text Explanation :
Workspace:
Which of the following statements MUST be true?
I. 10 is placed in a slot in Row 1.
II. 1 is placed in a slot in Row 4.
- (a)
Only II
- (b)
Neither I nor II
- (c)
Only I
- (d)
Both I and II
Answer: Option D
Text Explanation :
Workspace:
Which of the following statements MUST be true?
I. 2 is placed in a slot in Column 2.
II. 3 is placed in a slot in Column 3.
- (a)
Only II
- (b)
Neither I nor II
- (c)
Only I
- (d)
Both I and II
Answer: Option B
Text Explanation :
Workspace:
For how many slots in the grid, placement of numbers CANNOT be determined with certainty?
Answer: 2
Text Explanation :
Workspace:
What is the sum of the numbers placed in Column 4?
Answer: 26
Text Explanation :
Workspace:
Answer the following questions based on the information given below.
An online e-commerce firm receives daily integer product ratings from 1 through 5 given by buyers. The daily average is the average of the ratings given on that day. The cumulative average is the average of all ratings given on or before that day. The rating system began on Day 1, and the cumulative averages were 3 and 3.1 at the end of Day 1 and Day 2, respectively. The distribution of ratings on Day 2 is given in the figure below.

The following information is known about ratings on Day 3.
1. 100 buyers gave product ratings on Day 3.
2. The modes of the product ratings were 4 and 5.
3. The numbers of buyers giving each product rating are non-zero multiples of 10.
4. The same number of buyers gave product ratings of 1 and 2, and that number is half the number of buyers who gave a rating of 3.
How many buyers gave ratings on Day 1?
Answer: 150
Text Explanation :
Workspace:
What is the daily average rating of Day 3?
- (a)
3.0
- (b)
3.5
- (c)
3.2
- (d)
3.6
Answer: Option D
Text Explanation :
Workspace:
What is the median of all ratings given on Day 3?
Answer: 4
Text Explanation :
Workspace:
Which of the following is true about the cumulative average ratings of Day 2 and Day 3?
- (a)
The cumulative average of Day 3 increased by a percentage between 5% and 8% from Day 2.
- (b)
The cumulative average of Day 3 increased by more than 8% from Day 2.
- (c)
The cumulative average of Day 3 decreased from Day 2.
- (d)
The cumulative average of Day 3 increased by less than 5% from Day 2.
Answer: Option A
Text Explanation :
Workspace:
Answer the following questions based on the information given below:
Five restaurants, coded R1, R2, R3, R4 and R5 gave integer ratings to five gig workers – Ullas, Vasu, Waman, Xavier and Yusuf, on a scale of 1 to 5.
The means of the ratings given by R1, R2, R3, R4 and R5 were 3.4, 2.2, 3.8, 2.8 and 3.4 respectively.
The summary statistics of these ratings for the five workers is given below.
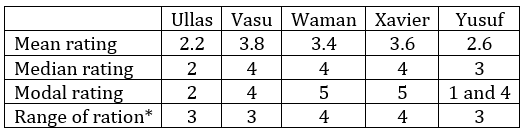
* Range of ratings is defined as the difference between the maximum and minimum ratings awarded to a worker.
The following is partial information about ratings of 1 and 5 awarded by the restaurants to the workers.
(a) R1 awarded a rating of 5 to Waman, as did R2 to Xavier, R3 to Waman and Xavier, and R5 to Vasu.
(b) R1 awarded a rating of 1 to Ullas, as did R2 to Waman and Yusuf, and R3 to Yusuf.
How many individual ratings cannot be determined from the above information?
Answer: 0
Text Explanation :
The means of the ratings given by R1, R2, R3, R4 and R5 were 3.4, 2.2, 3.8, 2.8 and 3.4 respectively.
∴ The sum of rating given by R1, R2, R3, R4 and R5 were 17, 11, 19, 14 and 17 respectively. (Multiplied with 5)
Similarly, we can find the sum of rating of all the 5 people.
Filling the data given in point 1 and 2, we get the following table:
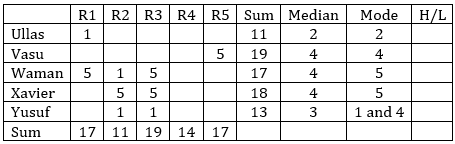
Range of ratings:
Ullas: lowest is given as 1, hence his highest = 1 + 3 = 4.
Vasu: highest is given as 5, hence his lowest = 5 – 3 = 2.
Waman: highest is 5 and lowest is 1.
Xavier: highest is given as 5, hence his lowest = 5 – 4 = 1.
Yusuf: lowest is given as 1, hence his highest = 1 + 3 = 4.
Ullas: Highest = 4, Lowest = 1, Median = 2 and Mode = 2
∴ Since median is 2, his reading in ascending order can be

Sum of reading of Ullas = 11, and his mode is 2
This is possible only when his readings in ascending order must be 1, 2, 2, 2, 4.
Vasu: Highest = 5, Lowest = 2, Median = 4 and Mode = 4.
∴ Since median is 4, his reading in ascending order can be

Sum of reading of Vasu = 19, and his mode is 2
This is possible when his readings in ascending order must be 2, 4, 4, 4, 5.
Waman: Highest = 5, Lowest = 1, Median = 4 and Mode = 5.
∴ Since median is 4, his reading in ascending order can be

Sum of reading of Waman = 17, and his mode is 5
This is possible when his readings in ascending order must be 1, 2, 4, 5, 5.
Xavier: Highest = 5, Lowest = 1, Median = 4 and Mode = 5.
∴ Since median is 4, his reading in ascending order can be

Sum of reading of Xavier = 18, and his mode is 5
This is possible when his readings in ascending order must be 1, 3, 4, 5, 5.
Yusuf: Highest = 4, Lowest = 1, Median = 3 and Mode = 1 and 4.
∴ Since median is 4, his reading in ascending order can be

Sum of reading of Yusuf = 17, and his mode is 1 and 4
This is possible when his readings in ascending order must be 1, 1, 3, 4, 4.
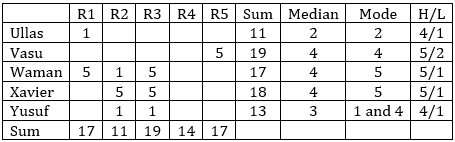
Now, we have the following table.

For R3, sum of ratings is 19, hence R3’s sum of rating for Ullas and Vasu = 19 – 5 – 5 – 1 = 8.
This is possible only when R3 gives a rating of 4 to both Ullas and Vasu.
For Ullas, the remaining 3 2’s would be given by R2, R4 and R5.

For R2, rating given to Vasu = 11 – 2 – 1 – 5 – 1 = 2.
∴ For Vasu the remaining 2 4s would be given by R1 and R4.
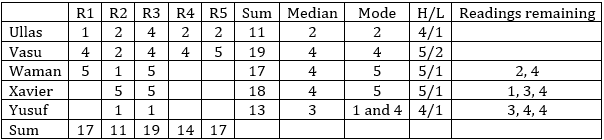
Xavier receives a rating of 1. This can only be given by R4. If R1 or R5 give a rating of 1 to Xavier, their sum of 17 each could not be achieved.
Now, the sum of ratings given by R4 to Waman and Yusuf = 14 – 2 – 4 – 1 = 7.
This is only possible when Waman gets a rating of 4 from R4 and Yusuf gets a rating of 3 from R4.
∴ The remaining rating of 2 for Waman must have come from R5.
∴ The remaining 2 4s for Yusuf must have come from R1 and R5.
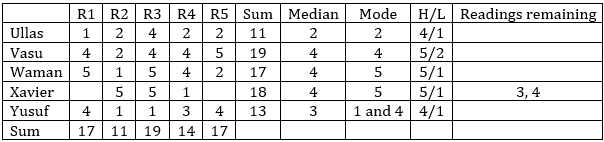
For R1, rating given to Xavier = 17 – 1 – 4 – 5 – 4 = 3
⇒ The remaining rating of 4 for Xavier must have been given by R5.

Ratings of all can be uniquely determined.
Hence, 0.
Workspace:
To how many workers did R2 give a rating of 4?
Answer: 0
Text Explanation :
Consider the solution to first question of this set.

R2 gave a rating of 4 to no one.
Hence, 0.
Workspace:
What rating did R1 give to Xavier?
Answer: 3
Text Explanation :
Consider the solution to first question of this set.

R1 gave a rating of 3 to Xavier.
Hence, 3.
Workspace:
What is the median of the ratings given by R3 to the five workers?
Answer: 4
Text Explanation :
Consider the solution to first question of this set.

R3 gave ratings of 1, 4, 4, 5, 5.
∴ Median rating is 4.
Hence, 4.
Workspace:
Which among the following restaurants gave its median rating to exactly one of the workers?
- (a)
R5
- (b)
R4
- (c)
R2
- (d)
R3
Answer: Option B
Text Explanation :
Consider the solution to first question of this set.

Median rating for:
R1 is 4, given to 2 persons.
R2 is 2, given to 2 persons.
R3 is 4, given to 2 persons.
R4 is 3, given to only 1 person.
R5 is 4, given to 2 persons.
∴ R4 gave median rating to only 1 person.
Hence, option (b).
Workspace:
Answer the following questions based on the information given below:
Odsville has five firms – Alfloo, Bzygoo, Czechy, Drjbna and Elavalaki. Each of these firms was founded in some year and also closed down a few years later.
Each firm raised Rs. 1 crore in its first and last year of existence. The amount each firm raised every year increased until it reached a maximum, and then decreased until the firm closed down. No firm raised the same amount of money in two consecutive years. Each annual increase and decrease was either by Rs. 1 crore or by Rs. 2 crores.
The table below provides partial information about the five firms.
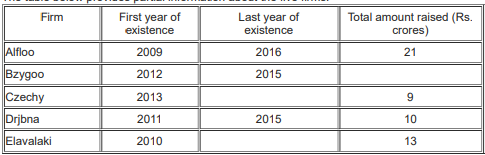
For which firm(s) can the amounts raised by them be concluded with certainty in each year?
- (a)
Only Czechy
- (b)
Only Bzygoo and Czechy and Drjbna
- (c)
Only Drjbna
- (d)
Only Czechy and Drjbna
Answer: Option D
Text Explanation :
We can represent the money raised each year for each company as follows.
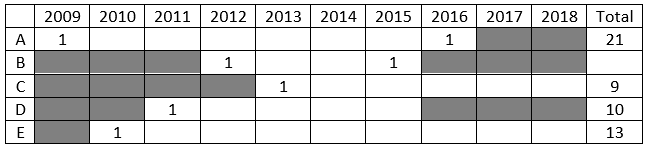
For each or these companies we will try to make cases satifying the given conditions.
We will write the amount of money raised by them in consecutive years from starting from their 1st year till their last year.
For A, the sum is 21 where first and last values must be 1.
This is possible for the following order of numbers.
Case 1: 1 → 2 → 3 → 4 → 5 → 3 → 2 → 1
Case 2: 1 → 2 → 3 → 5 → 4 → 3 → 2 → 1
For B, the only two possible order of numbers is
Case 1: 1 → 2 → 3 → 1
Case 2: 1 → 3 → 2 → 1
For C, the sum is 9 where first and last values must be 1.
This is only possible when the order of numbers is
1 → 2 → 3 → 2 → 1
For D, the sum is 10 where first and last values must be 1.
This is only possible when the order of numbers is
1 → 2 → 4 → 2 → 1
For E, the sum is 13 where first and last values must be 1.
This is possible for the following order of numbers.
Case 1: 1 → 2 → 4 → 3 → 2 → 1
Case 2: 1 → 2 → 3 → 4 → 2 → 1
Case 3: 1 → 3 → 5 → 3 → 1
Hence, we get the following table with all possible cases.
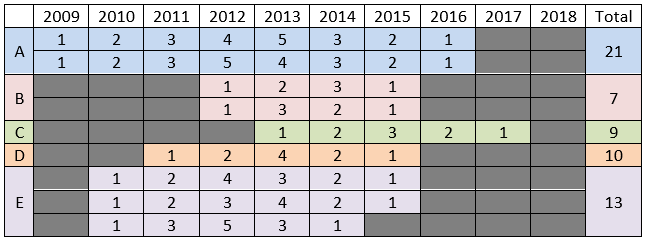
For C and D we can definitely determine the amounts raised by them each year.
Hence, option (d).
Workspace:
What best can be concluded about the total amount of money raised in 2015?
- (a)
It is either Rs. 7 crores or Rs. 8 crores or Rs. 9 crores.
- (b)
It is either Rs. 7 crores or Rs. 8 crores.
- (c)
It is exactly Rs. 8 crores.
- (d)
It is either Rs. 8 crores or Rs. 9 crores.
Answer: Option B
Text Explanation :
Consider the solution for the first questions of this set.

Amount of money raised in 2015 by:
A = 2
B = 1
C = 3
D = 1
E = 1 or 0
∴ Total money raised by them in 2015 = 2 + 1 + 3 + 1 + (1 or 0) = 8 or 7 crores.
Hence, option (b).
Workspace:
What is the largest possible total amount of money (in Rs. crores) that could have been raised in 2013?
Answer: 17
Text Explanation :
Consider the solution for the first questions of this set.

Highest amoun of money that can be raised in 2013 by:
A = 5
B = 3
C = 1
D = 4
E = 4
∴ Highest total amount of money that can be raised by them in 2013 = 5 + 3 + 1 + 4 + 4 = 17 crores.
Hence, 17.
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report