Coordinate Geometry - Previous Year IPM/BBA Questions

Answer: 140

Text Explanation :

​​​​​​​

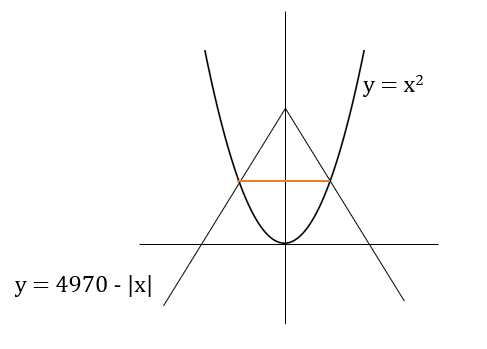
y = 4970 - |x| & y = x²

To find intersection point we equate both equations.
⇒ 4970 - |x| = x² 
⇒ x² + |x| - 4970 = 0
⇒ |x|² + |x| - 4970 = 0 [x² = |x|²]
⇒ |x|² + 71|x| - 70|x| - 4970 = 0
⇒ (|x| + 71)(|x| - 70) = 0
⇒ |x| = - 71 or 70 [- 71 rejeceted as |x| cannot be negative]

⇒ x = + 70 or - 70

∴ Line joining the intersection point of these graphs will be a horizontal line. The x coordinates of its end points are +70 & -70.
∴ Distance between the two points = 70 + 70 = 140.

Hence, 140.

Answer: 14

Text Explanation :

​​​​​​​

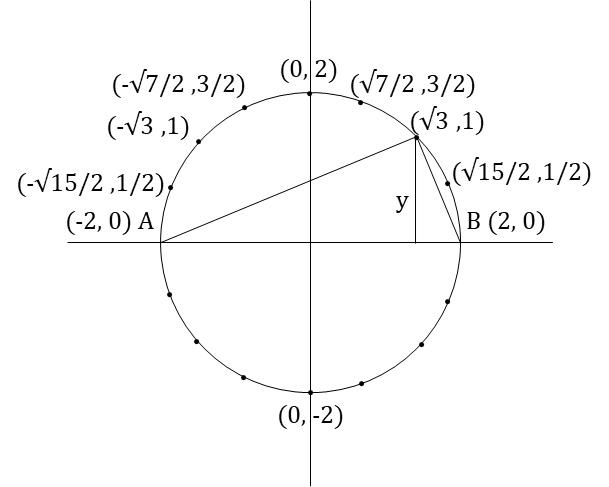
AB = 4

Based on the figure, area of triangel ABC = 1/2 × AB × |y| = 2|y|

∴ 2|y| must be an integer.

Hence, y can be

Case 1: y = ± 1/2
⇒ x² + (1/2)² = 4 
⇒ x² = 15/4
⇒ x = ± √15/2
∴ 4 points i.e, (√15/2 ,1/2), (-√15/2 ,1/2), (√15/2 ,-1/2) & (-√15/2 ,-1/2)

Case 2: y = ± 1
⇒ x² + (1)² = 4 
⇒ x² = 3
⇒ x = ± √3
∴ 4 points i.e, (√3 ,1), (-√3 ,1), (√3 ,-1) & (-√3 ,-1)

Case 1: y = ± 3/2
⇒ x² + (3/2)² = 4 
⇒ x² = 7/4
⇒ x = ± √7/2
∴ 4 points i.e, (√7/2 ,3/2), (-√7/2 ,3/2), (√7/2 ,-3/2) & (-√7/2 ,-3/2)

Case 1: y = ± 2
⇒ x² + (2)² = 4 
⇒ x² = 0
⇒ x = 0
∴ 2 points i.e, (0 ,2) & (0 ,-2)

∴ Total 4 + 4 + 4 + 2 = 14 points

Hence, 14.

Answer: Option D

Text Explanation :

Answer: Option C

Text Explanation :

Answer: 12

Text Explanation :

Consider, 2|x| + 3|y| = 6

Case 1: x > 0 and y > 0 [Quandrant I]
⇒ 2x + 3y = 6

Case 2: x < 0 and y > 0 [Quandrant II]
⇒ - 2x + 3y = 6

Case 3: x < 0 and y < 0 [Quandrant III]
⇒ - 2x - 3y = 6

Case 4: x > 0 and y < 0 [Quandrant IV]
⇒ 2x - 3y = 6

Each of these 4 lines can be drawn in their respective quadrants as shown in the figure.

​​​​​​​

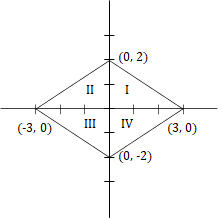
We need the area of region bounded by these 4 lines.

Area of region I = 1/2 × 3 × 2 = 3 sq. units

Similarly area of region II, III and IV = 3 sq. units each.

∴ Area of all the 4 regions combined = 3 + 3 + 3 + 3 = 12 sq. units

Hence, 12..

Answer: Option A

Text Explanation :

Equation $\frac{{\mathrm{x}}^2}{{\mathrm{a}}^2}+\frac{{\mathrm{y}}^2}{{\mathrm{b}}^2}=1$ represents an ellipse.

Hence, the given curve is an ellipse. We need to figure out the foci of this ellipse.

Also, Cos√2 - cos√3 > Sin√2 - Sin√3 > 0

⇒ b² > a²

∴ Foci is on y-axis.

Hence, option (a).

Answer: 26

Text Explanation :

The two given equations contain 3 lines.

Let the slope of common line between 2 equations be 'm'
Let the slope of remaining two perpendicular lines be b and -1/n.

Given, 2𝑥² + axy + 3y² = 0
⇒ $\frac{2}{3}{x}^2$ + $\frac{a}{3}xy$ + y² = (y - mx)(y - nx)
∴ m + n = $\frac{a}{3}$ ...(1) and mn = $\frac{2}{3}$   ...(2)

Also, 2𝑥² + bxy - 3y² = 0
⇒ $-\frac{2}{3}{x}^2$ - $\frac{b}{3}xy$ + y² = $\left(y-mx\right)\left(y+\frac{1}{n}x\right)$
∴ - m + $\frac{1}{n}$ = $-\frac{b}{3}$   ...(3)  and $-\frac{m}{n}$ = $-\frac{2}{3}$   ...(4)

Multiplying (2) and (4)
⇒ m² = 4/9

Case 1: m = + 2/3 ⇒ n = 1
⇒ a/3 = m + n ⇒ a = 5
⇒ - b/3 = - m + 1/n ⇒ b = 1

Case 2: m = - 2/3 ⇒ n = - 1
⇒ a/3 = m + n ⇒ a = - 5
⇒ -b/3 = - m + 1/n ⇒ b = - 1

In both cases: 𝑎² + 𝑏² = 25 + 1 = 26

Hence, 26.

Answer: Option D

Text Explanation :

The intersection of the lines x + 2y = 4 and 2x + 3y = 6 is (0, 2)

Slope of line 3x – y = 2 is 3. Slope of line perpendicular to this line is -1/3 [Product of slopes of two perpendicular lines = -1]

Now, we need to find the x-intercept of a line passing through (0, 2) whose slope is -1/3

Let the x-intercept be (a, 0)

⇒​ Slope of the line passing through (a, 0) and (0, 2) = - 1/3

⇒​ $\frac{0-2}{\mathrm{a}-0}$ = $-\frac{1}{3}$

⇒​ a = 6

Hence, option (d).

Answer: 4

Text Explanation :

The center of the given circle is at (0, 0) and its radius = 1.

​​​​​​​

The shortest distance between the point (-4, 3) and the circle = distance between (-4, 3) and the center - radius of the circle.

= OM - ON

= $\sqrt{{(-4-0)}^2+{(3-0)}^2}$ - 1

= 5 - 1

= 4.

Hence, 4.

Answer: Option A

Text Explanation :

Let the x-intercept and y-intercept of the line are B (a, 0) and A (0, b)

​​​​​​​

Since M (-5, 4) is the midpoint of these two intercepts, we have
-5 = (a + 0)/2 and 4 = (0 + b)/2
⇒ a = -10 and b = 8

∴ Equation of the line is: x/-10 + y/8 = 1
⇒ -8x + 10y = 80
⇒ 10y - 8x = 80

Hence, option (a).

Answer: 7

Text Explanation :

Answer: 54

Text Explanation :

Answer: Option A

Text Explanation :

2|x| + 3|y| = 6

Case 1: x > 0 and y > 0 [Quandrant I]
⇒ 2x + 3y = 6

Case 2: x < 0 and y > 0 [Quandrant II]
⇒ - 2x + 3y = 6

Case 3: x < 0 and y < 0 [Quandrant III]
⇒ - 2x - 3y = 6

Case 4: x > 0 and y < 0 [Quandrant IV]
⇒ 2x - 3y = 6

Each of these 4 lines can be drawn in their respective quadrants as shown in the figure.

​​​​​​​

Area of region I = 1/2 × 3 × 2 = 3 sq. units

Similarly area of region II, III and IV = 3 sq. units each.

∴ Area of all the 4 regions combined = 3 + 3 + 3 + 3 = 12 sq. units

Hence, option (a).

Answer: Option B

Text Explanation :

Answer: Option A

Text Explanation :