IPMAT (I) 2022 QASA | Previous Year IPMAT - Indore Paper
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
+ = 1 and y = x2 - 30, then the value of x2 + y2 is:
Answer: 72
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
Given, + = 1
⇒ + = 1
⇒ logxy + logyx = 2
Now, logxy and logyx are reciprocal of each other and their sum is 2. Sum of a number and its reciprocal is always greater than or equal to 2. Equality is true when the number and reciprocal are both equal to 1.
∴ logxy = 1
⇒ x = y
Now, y = x2 - 30 [y = x]
⇒ x2 - x - 30 = 0
⇒ (x - 6)(x + 5) = 0
⇒ x = 6 [x = -5 is rejected as log is not defined for negative numbers.]
∴ y = 6
∴ x2 + y2 = 62 + 62 = 72
Hence, 72.
Workspace:
The area enclosed by 2|x| + 3|y| ≤ 6 is ____________ sq. units.
Answer: 12
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
Consider, 2|x| + 3|y| = 6
Case 1: x > 0 and y > 0 [Quandrant I]
⇒ 2x + 3y = 6
Case 2: x < 0 and y > 0 [Quandrant II]
⇒ - 2x + 3y = 6
Case 3: x < 0 and y < 0 [Quandrant III]
⇒ - 2x - 3y = 6
Case 4: x > 0 and y < 0 [Quandrant IV]
⇒ 2x - 3y = 6
Each of these 4 lines can be drawn in their respective quadrants as shown in the figure.
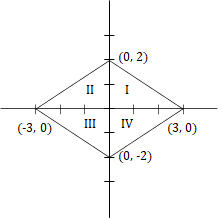
We need the area of region bounded by these 4 lines.
Area of region I = 1/2 × 3 × 2 = 3 sq. units
Similarly area of region II, III and IV = 3 sq. units each.
∴ Area of all the 4 regions combined = 3 + 3 + 3 + 3 = 12 sq. units
Hence, 12..
Workspace:
When Geeta increases her speed from 12km/hr to 20km/hr, she takes one hour less than the usual time to cover the distance between her home and office. The distance between her home and office is ___________ km.
Answer: 30
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
Let the times taken at 12 kmph is t hours, hence the time taken at 20 kmph is (t - 1) hours.
⇒ Distance = 12 × t = 20 × (t - 1)
⇒ 12t = 20t - 20
⇒ t = 2.5 hours.
∴ Distance = 12 × 2.5 = 30 kms.
Hence, 30.
Workspace:
The number of triangles that can be formed by choosing points from 7 points on a line and 5 points on another parallel line is _________.
Answer: 175
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
7 points lie on a line and 5 points on another parallel line.
A triangle can be formed by 2 points on one of these lines and third point on the other line.
Case 1: 2 points are chose on line with 7 points and 3rd point is chosen on line with 5 points.
⇒ Number of such triangles = 7C2 × 5C1 = 21 × 5 = 105
Case 2: 1 point is chose on line with 7 points and 2 points are chosen on line with 5 points.
⇒ Number of such triangles = 7C1 × 5C2 = 7 × 10 = 70
∴ Total number of traingles = 105 + 70 = 175.
Hence, 175.
Workspace:
Aruna purchases a certain number of apples for INR 20 each and a certain number of mangoes for INR 25 each. If she sells all the apples at 10% profit and all the mangoes at 20% loss, overall she makes neither profit nor loss. Instead, if she sells all the apples at 20% loss and all the mangoes at 10% profit, overall she makes a loss of INR 150 . Then the number of apples purchased by Aruna is _________.
Answer: 50
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
Let Aruna purchase x apples at 20 each and y mangoes at 25 each.
Total cost = 20x + 25y
Case 1:
Total selling price of apples = x × 20 × 1.1 = 22x
Total selling price of mangoes = y × 25 × 0.8 = 20y
Since Aruna had no profit or loss, total cost price = total selling price
∴ 20x + 25y = 22x + 20y
⇒ 5y = 2x
⇒ x : y = 5 : 2
∴ Let x = 5q and y = 2q ...(1)
Case 2:
Total selling price of apples = x × 20 × 0.8 = 16x
Total selling price of mangoes = y × 25 × 1.1 = 27.5y
Now Aruna incurred a loss of Rs. 150
∴ 20x + 25y - 150 = 16x + 27.5y
⇒ 4x - 150 = 2.5y
⇒ 20q - 150 = 5q
⇒ q = 10
∴ Number of apples bought by Aruna = x = 5q = 50.
Hence, 50.
Workspace:
Given that f(x) = |x| + 2|x−1| + |x−2| + |x−4| + |x−6| + 2|x−10|, x ∈ (−∞, ∞) the minimum value of f(x)
is _________.
Answer: 26
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
Given, f(x) = |x| + 2|x−1| + |x−2| + |x−4| + |x−6| + 2|x−10|
f(x) can be written as sum of h(x) and g(x), where
h(x) = |x| + |x−1| + |x−2| + |x−4| + |x−6| + |x−10| and
g(x) = |x−1| + |x−10|
For h(x) critical points are 0, 1, 2, 4, 6 and 10.
∴ h(x) will be least when x is between 2 and 4.
For g(x) critical points are 1 and 10.
∴ g(x) will be least when x is between 1 and 10.
∴ Both h(x) and g(x) will be least when x is between 2 and 4.
Let us take x = 3.
Least value of h(x) = 3 + 2 + 1 + 1 + 3 + 7 = 17
Least value of g(x) = 2 + 7 = 9
⇒ Least value of f(x) = 17 + 9 = 26.
Hence, 26.
Workspace:
If A = , then the absolute value of the determinant of (A9 + A6 + A3 + A) is __________.
Answer: 32
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
Given, A =
Now, A × A = × = = = I
⇒ A3 = A2 × A = I × A = A
⇒ A6 = A3 × A3 = A × A = I
⇒ A9 = A3 × A3 × A3 = A × A × A = A2 × A = I × A = A
Now, (A9 + A6 + A3 + A)
= A + I + A + A + A
= 3A + I
= +
=
∴ The absolute value of the determinant of (A9 + A6 + A3 + A) = absolute value of
= |4 × (1 × 1 - 3 × 3)| = |4 × (1 - 9)| = 32.
Hence, 32.
Workspace:
The sum of the coefficients of all the terms in the expansion of (5x − 9)4 is __________.
Answer: 256
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
Sum of the coefficients of all the terms in the expansion of (ax − b)n can be obtained by substituting x = 1.
∴ Sum of the coefficients of all the terms in the expansion of (5x − 9)4 = (5 - 9)4 = 44 = 256.
Hence, 256.
Workspace:
A new sequence is obtained from the sequence of positive integers (1,2,3,…) by deleting all the perfect squares. Then the 2022nd term of the new sequence is ________.
Answer: 2067
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
2022nd number in the sequence (including perfect squares) is 2022.
Now let us calculate number of perfect squares till 2022.
12, 22, 32, 42, 52, ..., 442 i.e., 44 numbers.
∴ 2022nd number will be 2022 + 44 = 2066.
Here we need to check if there is any perfect square between 2022 and 2066.
2025 i.e., 452 is a perfect square between 2022 and 2066.
⇒ 2022nd number in the given sequence after removing perfect squares will be 2067.
Hence, 2067.
Workspace:
Sin α + Sin β = and Cos α + Cos β = , then the value of is _______.
Answer: 100
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
Sin α + Sin β = ...(1) and
Cos α + Cos β = ...(2),
Squaring both the equations and adding them we get.
⇒ Sin2 α + Sin2 β + 2 × Sin α × Sin β + Cos2 α + Cos2 β + 2 × Cos α × Cos β = +
⇒ Sin2 α + Cos2 α + Sin2 β + Cos2 β + 2 × Sin α × Sin β + 2 × Cos α × Cos β = 1
⇒ 1 + 1 + 2 × cos (α - β) = 1
⇒ cos (α - β) = - 1/2
⇒ 2 × - 1 = - 1/2
⇒ = 1/4
∴ 202 × = 400
⇒ = 100.
Hence, 100.
Workspace:
The 3rd ,14th and 69th terms of an arithmetic progression form three distinct and consecutive terms of a geometric progression. If the next term of the geometric progression is the nth term of the arithmetic progression, then n equals ________.
Answer: 344
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
Let the 3rd term of AP = T3 = a [Here, a is not the first term of the AP]
14th term of AP = T14 = ar and
69th term of AP = T69 = ar2
Now, T14 - T3 = 11d [d is the common difference of the AP]
Also, T69 - T14 = 55d
⇒ 5(T14 - T3) = T69 - T14
⇒ 5(ar - a) = ar2 - ar
⇒ r2 - 6r + 5 = 0
⇒ (r - 1)(r - 5) = 0
⇒ r = 1 or 5
[r = 1 is rejected as the given terms are distinct.]
∴ T3 = a
T14 = 5a
T69 = 25a
⇒ d = (5a - a)/11 = 4a/11
Now, next term of geometric progression will be 125a = T3 + (n - 3)d
⇒ 125a = a + (n - 3) × 4a/11
⇒ 341 = n - 3
⇒ n = 344.
∴ The next term of the geometric progression is the 344th term of the GP.
Hence, 344.
Workspace:
Let P(X) denote power set of a set X. If A is the null set, then the number of elements in P(P(P(P(A)))) is _________.
Answer: 16
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
P(A) is the power set of A.
Number of elements in power set of A = 2n where n is the number of elements in A.
Since A is a null set, number of elements in P(A) = 20 = 1.
Power set of P(A) i.e., P(P(A)) will have 21 = 2 elements.
Power set of P(P(A)) i.e., P(P(P(A))) will have 22 = 4 elements.
Power set of P(P(P(A))) i.e., P(P(P(P(A)))) will have 24 = 16 elements.
Hence, 16.
Workspace:
The numbers −16, 2x+3 − 22x−1 − 16, 22x−1 + 16 are in an arithmetic progression. Then x equals ________.
Answer: 3
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
−16, 2x+3 − 22x−1 − 16, 22x−1 + 16 are in AP
If a, b and c are in AP ⇒ 2b = a + c
∴ 2 × (2x+3 − 22x−1 − 16) = -16 + 22x−1 + 16
⇒ 2x+4 − 22x − 32) = 22x−1
⇒ 16 × 2x − 22x − 32 = 22x/2
⇒ 32 × 2x − 2 × 22x − 64 = 22x
Take 2x = a and 22x = a2
⇒ 32a − 2a2 − 64 = a2
⇒ 3a2 - 32a + 64 = 0
⇒ 3a2 - 8a - 24a + 64 = 0
⇒ (3a - 8)(a - 8) = 0
⇒ a = 8/3 or 8
⇒ 2x = 8/3 or 8
[8/3 is rejected as 2x cannot be a fraction]
⇒ 2x = 8 = 23
⇒ x = 3
Hence, 3.
Workspace:
Mrs and Mr Sharma, and Mrs and Mr Ahuja along with four other persons are to be seated at a round table for dinner. If Mrs and Mr Sharma are to be seated next to each other, and Mrs and Mr Ahuja are not to be seated next to each other, then the total number of seating arrangements is _________.
Answer: 960
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
Let us form a group X of Mr. and Mr. Ahuja. They can be arranged in 2! = 2 ways.
Now, X and 4 other persons can be seated around a circle in 4! = 24 ways.
Now we have total 5 people (X is counted as 1 only, no one should sit between Ahujaas) and there are 5 places between these 5 people for Mr. and Mrs. Sharma to sit.
We need to select 2 of these 5 places for Mr. and Mrs. Sharma. This can be done in 5C2 = 10 ways.
Mr. and Mrs. Sharam can sit in these 2 places in 2! = 2 ways.
∴ Total number of ways = 2 × 24 × 10 × 2 = 960.
Hence, 960.
Workspace:
Let 50 distinct positive integers be chosen such that the highest among them is 100, and the average of the largest 25 integers among them exceeds the average of the remaining integers by 50 . Then the maximum possible value of the sum of all the 50 integers is _________.
Answer: 3150
Get your concepts cleared through our Self-Study Courses.
Join our Telegram Channel for CAT/MBA Preparation.
Explanation :
To calculate the maximum sum of 50 integers, we can assume the largest 25 integers as 100, 99, 98, ..., 76.
Average of these 25 integers = (100 + 76)/2 = 88
The average of remaining 25 integers must be 88 - 50 = 38
∴ Maximum sum of all 50 integers = 25 × 88 + 25 × 38 = 25 × 126 = 3150
Hence, 3150.
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report