CUET 2022 General Test inactie
A shopkeeper bought toffees at a rate of 10 for Rs. 15 and sold them at a rate of 16 for Rs. 40. Find his profit percentage?
- A.
65.05%
- B.
33.33%
- C.
50.55%
- D.
66.67%
Answer: Option D
Explanation :
CP of 1 toffee = 15/10 = Rs. 1.5
SP if 1 toffee = 40/16 = Rs. 2.5
∴ Profit % = × 100 = 66.67%
Hence, option (d).
Workspace:
The angle of depression of the boat from the most head of 180 m high plane is 60°. How far is the boat from the plane?
- A.
360 m
- B.
60√3 m
- C.
180√3 m
- D.
180 m
Answer: Option B
Explanation :
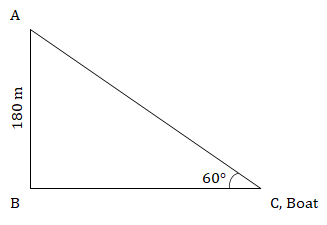
In ∆ABC,
Tan60° =
⇒ √3 = =
⇒ BC = = 60√3
Hence, option (b).
Workspace:
Find the value of the following expression:
- A.
- B.
1 8 - C.
- D.
Answer: Option A
Explanation :
Given,
=
=
=
= =
=
Hence, option (a).
Workspace:
Find the smallest number which should be added to the smallest number divisible by 6, 9 and 15 to make is a perfect square.
- A.
10
- B.
9
- C.
19
- D.
21
Answer: Option A
Explanation :
The smallest number divisible by 6, 9 and 15 = LCM (6, 9, 15) = 90
A perfect square just higher than 90 is 100. Hence, 10 must be added to make it a perfect square.
Hence, option (a).
Workspace:
The radii of two concentric circles with center O are 26 cm and 16 cm. Chord AB of the larger circle is tangent to the smaller circle at C and AD is a diameter. What is the length of CD?
- A.
42 cm
- B.
36 cm
- C.
35 cm
- D.
38 cm
Answer: Option D
Explanation :
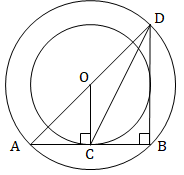
In right ∆AOC,
AC = = = = 2.
⇒ AB = 4√105
Now, since AD is the diameter, hence ∠ABD = 90° [Angle subtended by diameter on circle is always right angle.]
∴ In right ∆ABD
AD2 = AB2 + BD2
⇒ 522 = (4√105)2 + BD2
⇒ BD2 = 2704 – 1680 = 1024
⇒ BD = 32.
Now in ∆CBD
⇒ CD2 = CB2 + BD2
⇒ CD2 = 420 + 1024 = 1444
⇒ CD = 38
Hence, option (d).
Workspace:
Find the sum of the greatest and the smallest number which may replace k in the number 3281k6 to make the number divisible by 6.
- A.
9
- B.
8
- C.
5
- D.
4
Answer: Option B
Explanation :
To make 3281k6 divisible by 6, the number should be divisible by both 2 and 3.
Since, one’s digit of the number is even, the number is divisible by 2 for any value of k.
Now, to make the number also divisible by 3
⇒ 3 + 2 +8 + 1 +k + 6 = 20 + k should be divisible by 3.
∴ Smallest value of k = 1 while the greatest value = 7.
⇒ Required sum = 1 + 7 = 8
Hence, option (b).
Workspace:
A household appliances company offers two successive discounts of 20% and 35% on the sale of a food processor. What is the final sale price (in Rs. to the neared rupee) of a food processor costing Rs. 4580?
- A.
2519
- B.
2977
- C.
2382
- D.
3664
Answer: Option C
Explanation :
Initial price = Rs. 4580
Price after 20% discount = 4580 × 0.8 = Rs. 3664
Price after another 35% discount = 3664 × 0.65 = 2381.60
Hence, option (c).
Workspace:
If 5x - = 6, x > 0, then find the value of 25x2 - ?
- A.
6√41
- B.
36
- C.
√246
- D.
6√31
Answer: Option A
Explanation :
Given, 5x - = 6 ...(1)
Squaring both sides,
= 36
⇒ 25x2 + - 2 × 5x × = 36
⇒ 25x2 + + 2 × 5x × - 2 × 2 × 5x × = 36
⇒ - 5 = 36
⇒ = 41
⇒ 5x + = √41 ...(2)
From (1) × (2)
⇒ (5x)2 - = 6√41
Hence, option (a).
Workspace:
In triangle ABC, the bisector of angle BAC meets BC at point D in such a way that AB = 10 cm, AC = 15 cm and BD = 6 cm. Find the length of BC (in cm.)
- A.
17
- B.
11
- C.
15
- D.
9
Answer: Option C
Explanation :
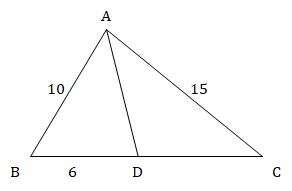
In ∆ABC, using angle bisector theorem,
⇒ AB/AC = BD/CD
⇒ 10/15 = 6/CD
⇒ CD = 9 cm.
∴ BC = 6 + 9 = 15 cm.
Hence, option (c).
Workspace:
A and B working alone can complete a work in 8 days and 12 days respectively. They started working together, but A left 2 days before completion of the work. In how many days was the work completed
- A.
6
- B.
5
- C.
8
- D.
10
Answer: Option A
Explanation :
Let the work be completed in ‘d’ days.
⇒ B worked for d days while A worked for (d – 2) days.
∴ Total work done = Work done by A + Work done by B
⇒ 1 = 1/8 × (d - 2) + 1/12 × d
⇒ 24 = 3(d - 2) + 2d
⇒ 30 = 5d
⇒ d = 6 days.
Hence, option (a).
Workspace:
Person A started a business by investing Rs. 65000. After a few months, B joined him by investing Rs. 50,000. Three months after the joining of B, C joined the two with an investment of Rs. 55,000. At the end of the year, A got 50% of the profit as his share. For how many months did A alone finance the business?
- A.
2
- B.
3
- C.
5
- D.
4
Answer: Option B
Explanation :
Let B invests for ‘m’ months.
⇒ A invests Rs. 65,000 for 12 months,
B invested Rs. 50,000 for m months,
C invested Rs. 55,000 for (m – 3) months.
⇒ PA : PB : PC = 65000 × 12 : 50000 × m : 55000 × (m - 3)
⇒ PA : PB : PC = 156 : 10m : 11(m – 3)
Given, PA is 50%
⇒ 156 = 10m + 11(m - 3)
⇒ 156 = 21m – 33
⇒ 189 = 21m
⇒ m = 9
⇒ B invested for 9 months, i.e., B joined 3 months after A started the business.
Hence, option (b).
Workspace:
The following bar graph shows receipts and expenditure by a business firm over 5 years.
Gain = Receipts – Expenditure
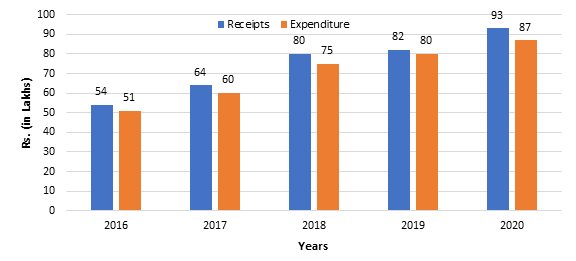
In which year did the company gain the minimum amount?
- A.
2016
- B.
2017
- C.
2019
- D.
2018
Answer: Option C
Explanation :
Gain in
2016: 54 – 51 = Rs. 3 lakh
2017: 64 – 60 = Rs. 4 lakh
2018: 80 – 75 = Rs. 5 lakh
2019: 82 – 80 = Rs. 2 lakh
∴ Company gained minimum amount of Rs. 2 lakh in 2019.
Hence, option (c).
Workspace:
Three positive numbers are in the ratio 2 : 3 : 4. The sum of their squares is 2349. The average of the first two numbers is:
- A.
36
- B.
27.5
- C.
18
- D.
22.5
Answer: Option D
Explanation :
Let the three numbers be 2x, 3x and 4x.
⇒ (2x)2 + (3x)2 + (4x)2 = 2349
⇒ 4x2 + 9x2 + 16x2 = 2349
⇒ 29x2 = 2349
⇒ x2 = 81
⇒ x = 9
∴ The average of first two numbers = (2x + 3x)/2 = 2.5 × 9 = 22.5
Hence, option (d).
Workspace:
The sides of a triangular field are 360 m, 480 m and 600 m. Its area is equal to the area of a square field. What is the side (in m) of the square field?
- A.
120√6
- B.
160√6
- C.
160√3
- D.
120√3
Answer: Option A
Explanation :
The ratio of sides of the triangle is 360 : 480 : 600 = 3 : 4 : 5.
Hence, it is a right triangle.
⇒ Area of the triangle = 1/2 × 360 × 480
Area of a square of side a = a2 = 1/2 × 360 × 480
⇒ a2 = 360 × 240
⇒ a =
⇒ a =
⇒ a = 120√6
Hence, option (a).
Workspace:
A person’s salary was decreased by 50% and subsequently increased by 50%. By what percent does his salary increase or decrease?
- A.
Decrease 18%
- B.
Increase 15%
- C.
Increase 20%
- D.
Decrease 25%
Answer: Option D
Explanation :
Net change = 50 – 50 + = -25%
Hence, option (d).
Workspace:
In a ∆ABC, D, E and F are the mid-points of side BC, CA and AB respectively. If BC = 25.6 cm, CA = 18.8 cm and AB = 20.4 cm, what is the perimeter (in cm) of the ∆DEF?
- A.
36.8
- B.
30.6
- C.
32.4
- D.
34.4
Answer: Option C
Explanation :
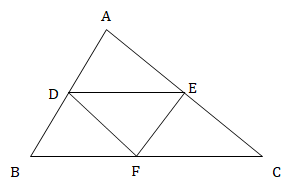
Since, D, E and F are the mid points.
DE = ½ × BC = 12.8
EF = ½ × AB = 10.2
FD = ½ × AC = 9.4
∴ DE + EF + FD = 12.8 + 10.2 + 9.4 = 32.4
Hence, option (c).
Workspace:
Find the value of the following expression: ?
- A.
7.06
- B.
7
- C.
7.33
- D.
6.73
Answer: Option D
Explanation :
0.027 = (0.3)3
⇒ =
We know, a3 – b3 = (a - b)(a2 – ab + b2)
⇒ = = 7.03 – 0.3 = 6.73
Hence, option (d).
Workspace:
Anil lent a sum of Rs. 5000 on simple interest for 10 years in such a way that the rate of interest is 6% p.a. for the first 2 years, 8% p.a. for the next 2 years and 10% p.a. beyond 4 years. How much interest (in Rs.) will he earn at the end of 10 years.
- A.
5000
- B.
4400
- C.
4200
- D.
3500
Answer: Option B
Explanation :
6% for 2 years:
Interest accumulated = = Rs. 600
8% for 2 years:
Interest accumulated = = Rs. 800
10% for 6 years:
Interest accumulated = = Rs. 3000
Total interest accumulated = 600 + 800 + 3000 = Rs. 4400
Hence, option (b).
Workspace:
The breakup of the total number of employees of a company working in different offices (A to E), in degree, is given in the pie-chart.
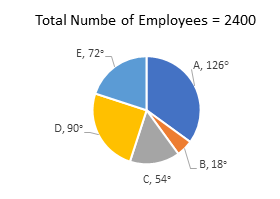
If 40% of the number of employees in office A are shifted equally to office B and E, then what will be the sum of the number of employees in B and C?
- A.
648
- B.
735
- C.
545
- D.
72
Answer: Option A
Explanation :
40% of 126° = 50.4°
Degree measure of B = 18 + 25.2 = 43.2°
Degree measure of C = 54°
Required number of employees = × 2400 = 648
Hence, option (a).
Workspace:
O is the center of a circle of radius 10 cm. P is a point outside the circle and PQ is a tangent to the circle. What is the length (in cm) of PQ if the OP is 26 cm?
- A.
2√194
- B.
20
- C.
25
- D.
24
Answer: Option D
Explanation :
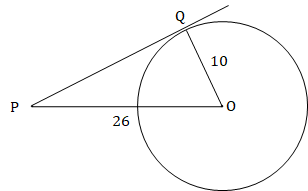
In right ∆OQP,
OP2 = OQ2 + PQ2
⇒ 262 = 102 + PQ2
⇒ PQ2 = 676 – 100 = 576
⇒ PQ = 24
Hence, option (d).
Workspace:
If A = 30°, what is the value of:
- A.
- B.
- C.
- D.
Answer: Option B
Explanation :
Given,
= = = =
Hence, option (b).
Workspace:
The distance between two stations A and B is 200 kms. A train runs from A to B at a speed of 75 kmph, while another train runs from B to A at a speed of 85 kmph. What will be the distance between the two trains (in kms) 3 minutes before they meet?
- A.
5
- B.
8
- C.
10
- D.
6
Answer: Option B
Explanation :
The distance between the trains 3 minutes before meeting can be calculated if we consider the situation in reverse direction.
Let the two trains be standing together and they start moving in opposite directions. The distance between them after 3 minutes = (75 + 85) × 3/60 = 8 kms.
Hence, option (b).
Workspace:
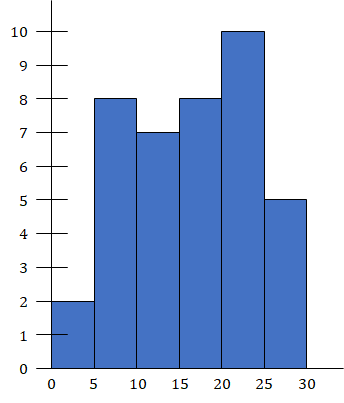
The following histogram show the marks scored by 40 students in a test of 30 marks. A student has to score a minimum of 10 marks to pass the test. What is the percentage of students who passed the test?
- A.
75%
- B.
30%
- C.
72%
- D.
66.66%
Answer: Option A
Explanation :
% of students who passed the test = × 100 = 75%
Hence, option (a).
Workspace:
Performance of 1800 students in grades has been shown in the following pie-chart.
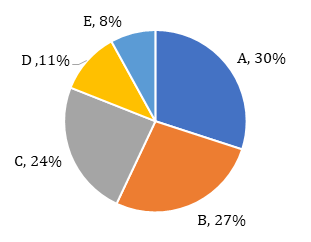
The number of students getting grade B is what percentage of the number of students getting grade A?
- A.
97%
- B.
90%
- C.
95%
- D.
85%
Answer: Option B
Explanation :
Required % = 27/30 × 100 = 90%
Hence, option (b).
Workspace:
If (2cosA + 1)(2cosA – 1) = 0, 0° < A ≤ 90°, then find the value of A.
- A.
90°
- B.
45°
- C.
30°
- D.
60°
Answer: Option C
Explanation :
(2cosA + 1)(2cosA – 1) = 0
⇒ 4cos2A - 1 = 0
⇒ 4cos2A – (cos2A + sin2A) = 0
⇒ 3cos2A – sin2A = 0
⇒ 3cos2A = sin2A
⇒ =3
⇒ tan2A = 3
⇒ tanA = √3
∴ A = 60°
Hence, option (c).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Ask Your Doubt
Ask Your Doubt Report
Report