LR - Board Games - Previous Year CAT/MBA Questions
The best way to prepare for LR - Board Games is by going through the previous year LR - Board Games CAT questions. Here we bring you all previous year LR - Board Games CAT questions along with detailed solutions.
Click here for previous year questions of other topics.
It would be best if you clear your concepts before you practice previous year LR - Board Games CAT questions.
Answer the following questions based on the information given below.

The above is a schematic diagram of walkways (indicated by all the straight-lines) and lakes (3 of them, each in the shape of rectangles – shaded in the diagram) of a gated area. Different points on the walkway are indicated by letters (A through P) with distances being OP = 150 m, ON = MN = 300 m, ML = 400 m, EL = 200 m, DE = 400 m.
The following additional information about the facilities in the area is known.
1. The only entry/exit point is at C.
2. There are many residences within the gated area; all of them are located on the path AH and ML with four of them being at A, H, M, and L.
3. The post office is located at P and the bank is located at B.
One resident whose house is located at L, needs to visit the post office as well as the bank. What is the minimum distance (in m) he has to walk starting from his residence and returning to his residence after visiting both the post office and the bank?
- (a)
3000
- (b)
2700
- (c)
3100
- (d)
3200
Answer: Option D
Text Explanation :
Workspace:
One person enters the gated area and decides to walk as much as possible before leaving the area without walking along any path more than once and always walking next to one of the lakes. Note that he may cross a point multiple times. How much distance (in m) will he walk within the gated area?
- (a)
3200
- (b)
3800
- (c)
2800
- (d)
3000
Answer: Option B
Text Explanation :
Workspace:
One resident takes a walk within the gated area starting from A and returning to A without going through any point (other than A) more than once. What is the maximum distance (in m) she can walk in this way?
Answer: 5100
Text Explanation :
Workspace:
Visitors coming for morning walks are allowed to enter as long as they do not pass by any of the residences and do not cross any point (except C) more than once. What is the maximum distance (in m) that such a visitor can walk within the gated area?
Answer: 3500
Text Explanation :
Workspace:
Answer the following questions based on the information given below.
The figure below shows a network with three parallel roads represented by horizontal lines R-A, R-B, and R-C and another three parallel roads represented by vertical lines V1, V2, and V3. The figure also shows the distance (in km) between two adjacent intersections. Six ATMs are placed at six of the nine road intersections. Each ATM has a distinct integer cash requirement (in Rs. Lakhs), and the numbers at the end of each line in the figure indicate the total cash requirements of all ATMs placed on the corresponding road. For example, the total cash requirement of the ATM(s) placed on road R-A is Rs. 22 Lakhs.
The following additional information is known.
1. The ATMs with the minimum and maximum cash requirements of Rs. 7 Lakhs and Rs. 15 Lakhs are placed on the same road.
2. The road distance between the ATM with the second highest cash requirement and the ATM located at the intersection of R-C and V3 is 12 km.

Which of the following statements is correct?
- (a)
The cash requirement of the ATM placed at the (R-C, V2) intersection cannot be uniquely determined.
- (b)
The ATM placed at the (R-C, V2) intersection has a cash requirement of Rs. 8 Lakhs.
- (c)
The ATM placed at the (R-C, V2) intersection has a cash requirement of Rs. 9 Lakhs.
- (d)
There is no ATM placed at the (R-C, V2) intersection.
Answer: Option C
Text Explanation :
Workspace:
How many ATMs have cash requirements of Rs. 10 Lakhs or more?
Answer: 3
Text Explanation :
Workspace:
Which of the following two statements is/are DEFINITELY true?
Statement A: Each of R-A, R-B, and R-C has two ATMs.
Statement B: Each of V1, V2, and V3 has two ATMs.
- (a)
Only Statement A
- (b)
Both Statement A and Statement B
- (c)
Neither Statement A nor Statement B
- (d)
Only Statement B
Answer: Option A
Text Explanation :
Workspace:
What best can be said about the road distance (in km) between the ATMs having the second highest and the second lowest cash requirements?
- (a)
Either 4 km or 7 km
- (b)
5 km
- (c)
7 km
- (d)
4 km
Answer: Option A
Text Explanation :
Workspace:
What is the number of ATMs whose locations and cash requirements can both be uniquely determined?
Answer: 3
Text Explanation :
Workspace:
Answer the next 4 questions based on the information given below.
Twenty-five coloured beads are to be arranged in a grid comprising of five rows and five columns. Each cell in the grid must contain exactly one bead. Each bead is coloured either Red, Blue or Green.
While arranging the beads along any of the five rows or along any of the five columns, the rules given below are to be followed:
- Two adjacent beads along the same row or column are always of different colors.
- There is at least one Green bead between any two Blue beads along the same row or column.
- There is at least one Blue and at least one Green bead between any two Red beads along the same row or column.
Every unique, complete arrangement of twenty-five beads is called a configuration.
The total number of possible configurations using beads of only two colors is:
Answer: 2
Text Explanation :
We can use beads of only two colors.
Since there must be a blue and a green bead between two red beads, we cannot choose one the two colors as red.
Hence, the two colors that can be used are green and blue.
Also, two adjacent beads along the same row or column are always of different colors. Hence, blue and green beads can only be placed alternately.
∴ The following 2 configurations are possible.
Configuration 1:

Configuration 2:

Hence, 2.
Workspace:
What is the maximum possible number of Red beads that can appear in any configuration?
Answer: 9
Text Explanation :
There must be a blue and a green bead between two red beads, we cannot choose one the two colors as red, and
There is at least one Green bead between any two Blue beads along the same row or column.
∴ We can have maximum two red beads in any row or column.
Consider the following configuration
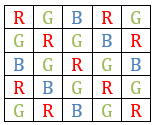
∴ The maximum number of red beads that can be used is 9.
Hence, 9.
Workspace:
What is the minimum number of Blue beads in any configuration?
Answer: 6
Text Explanation :
To minimize blue beads, we have to use maximum number of red and green beads.
There must be a blue and a green bead between two red beads, we cannot choose one the two colors as red, and
There is at least one green bead between any two blue beads along the same row or column.
Consider the configuration in the previous questions or this new configuration below.
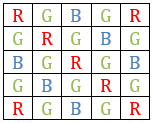
Hence, 6.
Workspace:
Two Red beads have been placed in ‘second row, third column’ and ‘third row, second column’. How many more Red beads can be placed so as to maximize the number of Red beads used in the configuration?
Answer: 6
Text Explanation :
According to the information given in the questions:
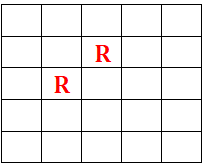
To maximum the number of red beads we can place the remaining beads in the following manner.
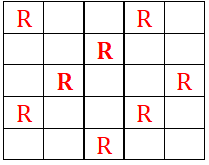

∴ Maximum 6 more red beads can be placed.
Hence, 6.
Workspace:
Answer the following questions based on the information given below.
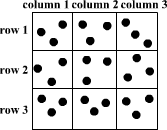
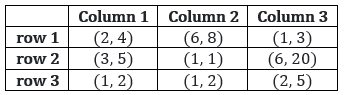
Three pouches (each represented by a filled circle) are kept in each of the nine slots in a 3 × 3 grid, as shown in the figure. Every pouch has a certain number of one-rupee coins. The minimum and maximum amounts of money (in rupees) among the three pouches in each of the nine slots are given in the table. For example, we know that among the three pouches kept in the second column of the first row, the minimum amount in a pouch is Rs. 6 and the maximum amount is Rs. 8.
There are nine pouches in any of the three columns, as well as in any of the three rows. It is known that the average amount of money (in rupees) kept in the nine pouches in any column or in any row is an integer. It is also known that the total amount of money kept in the three pouches in the first column of the third row is Rs. 4.
What is the total amount of money (in rupees) in the three pouches kept in the first column of the second row?
Answer: 13
Text Explanation :
Consider C1R1: Maximum coins in a pouch = 4 and minimum coins = 2. The third bag could have 2, 3 or 4 coins. Therefore, sum = 8, 9 or 10
Consider C1R2: Maximum coins in a pouch = 5 and minimum coins = 3. The third bag could have 3, 4 or 5 coins. Therefore, sum = 11, 12 or 13
Consider C1 R3: Maximum coins in a pouch = 2 and minimum coins = 1. As the sum = 4, third pouch has 1 coin.
As the sum of coins in the nine pouches in the column are divisible by 9, the coins in C1R1 and C1R2 has to be 10 (i.e., 2, 4, 4) and 13 (i.e., 3, 5, 5) respectively.
Consider column 2:
C2R1: Maximum coins in a pouch = 8 and minimum coins = 6. The third bag could have 6, 7 or 8 coins. Therefore, sum = 20, 21 or 22
C2R2: All the three pouches have one coin each. Sum = 3
C2R3: Maximum coins in a pouch = 2 and minimum coins = 1. The third bag could have 1 or 2 coins. Therefore, sum = 1 or 4
In order to have number of coins in the cells of the column divisible by 9, sum of the coins in C2R1 = 20(i.e., 6, 6, 8) and in C2R3 = 4(i.e., 1,1,2)
Now consider R1
First two cells together have 30 coins. So the third cell has to have 6(i.e., 1, 2, 3) coins.
Consider R2: First two cells together have 16 coins. Coins in the third cell are in the range 6 + 6 + 20 = 32 to 6 + 20 + 20 = 46. Therefore the third cell has to have 38 (i.e., 6, 12, 20) coins.
Consider R3: First two cells together have 8 coins. So the third cell has to have 10 (i.e., 2, 3, 5) coins.
Thus, we have

First column of the second row has 13 coins. i.e., Rs. 13
Answer: 13
Workspace:
How many pouches contain exactly one coin?
Answer: 8
Text Explanation :
Consider C1R1: Maximum coins in a pouch = 4 and minimum coins = 2. The third bag could have 2, 3 or 4 coins. Therefore, sum = 8, 9 or 10
Consider C1R2: Maximum coins in a pouch = 5 and minimum coins = 3. The third bag could have 3, 4 or 5 coins. Therefore, sum = 11, 12 or 13
Consider C1 R3: Maximum coins in a pouch = 2 and minimum coins = 1. As the sum = 4, third pouch has 1 coin.
As the sum of coins in the nine pouches in the column are divisible by 9, the coins in C1R1 and C1R2 has to be 10 (i.e., 2, 4, 4) and 13 (i.e., 3, 5, 5) respectively.
Consider column 2:
C2R1: Maximum coins in a pouch = 8 and minimum coins = 6. The third bag could have 6, 7 or 8 coins. Therefore, sum = 20, 21 or 22
C2R2: All the three pouches have one coin each. Sum = 3
C2R3: Maximum coins in a pouch = 2 and minimum coins = 1. The third bag could have 1 or 2 coins. Therefore, sum = 1 or 4
In order to have number of coins in the cells of the column divisible by 9, sum of the coins in C2R1 = 20(i.e., 6, 6, 8) and in C2R3 = 4(i.e., 1,1,2)
Now consider R1
First two cells together have 30 coins. So the third cell has to have 6(i.e., 1, 2, 3) coins.
Consider R2: First two cells together have 16 coins. Coins in the third cell are in the range 6 + 6 + 20 = 32 to 6 + 20 + 20 = 46. Therefore the third cell has to have 38 (i.e., 6, 12, 20) coins.
Consider R3: First two cells together have 8 coins. So the third cell has to have 10 (i.e., 2, 3, 5) coins.
Thus, we have

Two pouches in Row 3 Column 1 slot have 1 coin each.
Three pouches in Row 2 Column 2 have 1 coin each.
Two pouches in Row 3 Column 3 slot have 1 coin each.
One pouch in Row 1 Column 3 slot has 1 coin.
Total number of pouches = 2 + 3 + 2 + 1 = 8
Answer: 8
Workspace:
What is the number of slots for which the average amount (in rupees) of its three pouches is an integer?
Answer: 2
Text Explanation :
Consider C1R1: Maximum coins in a pouch = 4 and minimum coins = 2. The third bag could have 2, 3 or 4 coins. Therefore, sum = 8, 9 or 10
Consider C1R2: Maximum coins in a pouch = 5 and minimum coins = 3. The third bag could have 3, 4 or 5 coins. Therefore, sum = 11, 12 or 13
Consider C1 R3: Maximum coins in a pouch = 2 and minimum coins = 1. As the sum = 4, third pouch has 1 coin.
As the sum of coins in the nine pouches in the column are divisible by 9, the coins in C1R1 and C1R2 has to be 10 (i.e., 2, 4, 4) and 13 (i.e., 3, 5, 5) respectively.
Consider column 2:
C2R1: Maximum coins in a pouch = 8 and minimum coins = 6. The third bag could have 6, 7 or 8 coins. Therefore, sum = 20, 21 or 22
C2R2: All the three pouches have one coin each. Sum = 3
C2R3: Maximum coins in a pouch = 2 and minimum coins = 1. The third bag could have 1 or 2 coins. Therefore, sum = 1 or 4
In order to have number of coins in the cells of the column divisible by 9, sum of the coins in C2R1 = 20(i.e., 6, 6, 8) and in C2R3 = 4(i.e., 1,1,2)
Now consider R1
First two cells together have 30 coins. So the third cell has to have 6(i.e., 1, 2, 3) coins.
Consider R2: First two cells together have 16 coins. Coins in the third cell are in the range 6 + 6 + 20 = 32 to 6 + 20 + 20 = 46. Therefore the third cell has to have 38 (i.e., 6, 12, 20) coins.
Consider R3: First two cells together have 8 coins. So the third cell has to have 10 (i.e., 2, 3, 5) coins.
Thus, we have

For average amount to be an integer, we need to consider slots having total number of coins in the pouches divisible by 3.
There are two such slot i.e., (row 1 column 3) and (row 2 column 2).
Answer: 2.
Workspace:
The number of slots for which the total amount in its three pouches strictly exceeds Rs. 10 is
Answer: 3
Text Explanation :
Consider C1R1: Maximum coins in a pouch = 4 and minimum coins = 2. The third bag could have 2, 3 or 4 coins. Therefore, sum = 8, 9 or 10
Consider C1R2: Maximum coins in a pouch = 5 and minimum coins = 3. The third bag could have 3, 4 or 5 coins. Therefore, sum = 11, 12 or 13
Consider C1 R3: Maximum coins in a pouch = 2 and minimum coins = 1. As the sum = 4, third pouch has 1 coin.
As the sum of coins in the nine pouches in the column are divisible by 9, the coins in C1R1 and C1R2 has to be 10 (i.e., 2, 4, 4) and 13 (i.e., 3, 5, 5) respectively.
Consider column 2:
C2R1: Maximum coins in a pouch = 8 and minimum coins = 6. The third bag could have 6, 7 or 8 coins. Therefore, sum = 20, 21 or 22
C2R2: All the three pouches have one coin each. Sum = 3
C2R3: Maximum coins in a pouch = 2 and minimum coins = 1. The third bag could have 1 or 2 coins. Therefore, sum = 1 or 4
In order to have number of coins in the cells of the column divisible by 9, sum of the coins in C2R1 = 20(i.e., 6, 6, 8) and in C2R3 = 4(i.e., 1,1,2)
Now consider R1
First two cells together have 30 coins. So the third cell has to have 6(i.e., 1, 2, 3) coins.
Consider R2: First two cells together have 16 coins. Coins in the third cell are in the range 6 + 6 + 20 = 32 to 6 + 20 + 20 = 46. Therefore the third cell has to have 38 (i.e., 6, 12, 20) coins.
Consider R3: First two cells together have 8 coins. So the third cell has to have 10 (i.e., 2, 3, 5) coins.
Thus, we have

The slots for which the total amount in its three pouches strictly exceeds Rs. 10 are Row 1 Column 2, Row 2 Column 1, Row 2 Column 3.
Answer: 3.
Workspace:
Answer the following question based on the information given below.
You are given an n × n square matrix to be filled with numerals so that no two adjacent cells have the same numeral. Two cells are called adjacent if they touch each other horizontally, vertically or diagonally. So a cell in one of the four corners has three cells adjacent to it, and a cell in the first or last row or column which is not in the corner has five cells adjacent to it. Any other cell has eight cells adjacent to it.
What is the minimum number of different numerals needed to fill a 3×3 square matrix?
Answer: 4
Text Explanation :
A number say ‘x’ can be filled in four corner cells. Another number say ‘y’ can be used in the central cell. Now the remaining cells are middle cells of top row, bottom row, left column and right column. Two more numerals can be used to fill these cells. Assume that ‘z’ and ‘w’ are those numerals.
Thus,

Thus, four different numerals are required.
Therefore, the required answer is 4.
Answer: 4
Workspace:
What is the minimum number of different numerals needed to fill a 5 × 5 square matrix?
Answer: 4
Text Explanation :
A number say ‘x’ can be filled in four corner cells. Another number say ‘y’ can be used in the central cell. Now the remaining cells are middle cells of top row, bottom row, left column and right column. Two more numerals can be used to fill these cells. Assume that ‘z’ and ‘w’ are those numerals.
Thus,

So, at least 4 different numerals are required for a 3 × 3 matrix.
Top row i.e., the first row of the 5 × 5 matrix can be (x, z, x, z, x). Similarly, other cells from the second and the third row can be filled.
For the first column i.e., the leftmost column, the fourth cell from top can be filled with the number from the second cell from top i.e. w and the bottom cell can be filled with the number from the top most cell of the column i.e., x. Similarly, remaining cells of the remaining columns can be filled.
Thus, four different numerals are sufficient to fill a 5 × 5 matrix.
Therefore, the required answer is 4.
Answer: 4
Workspace:
Suppose you are allowed to make one mistake, that is, one pair of adjacent cells can have the same numeral. What is the minimum number of different numerals required to fill a 5×5 matrix?
- (a)
9
- (b)
16
- (c)
25
- (d)
4
Answer: Option D
Text Explanation :
A number say ‘x’ can be filled in four corner cells. Another number say ‘y’ can be used in the central cell. Now the remaining cells are middle cells of top row, bottom row, left column and right column. Two more numerals can be used to fill these cells. Assume that ‘z’ and ‘w’ are those numerals.
Thus,

4 different numerals are required to fill a 5 × 5 matrix. As one is allowed to make only one mistake, it is possible to change exactly one entry such that all other conditions are not violated.
Hence, option (d).
Workspace:
Suppose that all the cells adjacent to any particular cell must have different numerals. What is the minimum number of different numerals needed to fill a 5×5 square matrix?
- (a)
25
- (b)
16
- (c)
9
- (d)
4
Answer: Option C
Text Explanation :
Assuming that the particular cell is not a cell at one of the corner, it has 8 adjacent cells.
Hence, 8 + 1 = 9 different numerals are required to fill the particular cell and the adjacent cells.
Earlier we have seen that 4 different numerals are required to fill a 5 × 5 matrix. Hence, 9 different numerals will be definitely sufficient to fill the 5 × 5 matrix.
Hence, option (c).
Workspace:
Answer the following question based on the information given below.
In an 8 × 8 chessboard a queen placed anywhere can attack another piece if the piece is present in the same row, or in the same column or in any diagonal position in any possible 4 directions, provided there is no other piece in between in the path from the queen to that piece.
The columns are labelled a to h (left to right) and the rows are numbered 1 to 8 (bottom to top). The position of a piece given by the combination of column and row labels. For example, position c5 means that the piece is cth column and 5th row.
If the queen is at c5, and the other pieces at positions c2, g1, g3, g5 and a3, how many are under attack by the queen? There are no other pieces on the board.
- (a)
2
- (b)
3
- (c)
4
- (d)
5
Answer: Option C
Text Explanation :
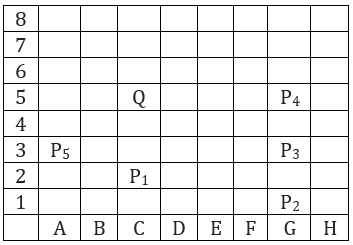
In the diagram given above let Q represent the queen at cell C5. Now let us suppose pieces P1, P2, P3, P4 and P5 are at cells. C2, G1, G3, G5 and A3. As can seen that Q can attack P1 as they are is the same column and can attack P4 as both are in the same row. Further Q can attack P5 and P2 as both are in a diagonal position to Q. So it cannot be attacked by Q. So 4 pieces i.e., P1, P2, P4 and P5 can attacked by Q.
Hence, option (c).
Workspace:
If the other pieces are only at positions a1, a3, b4, d7, h7 and h8, then which of the following positions of the queen results in the maximum number of pieces being under attack?
- (a)
f8
- (b)
a7
- (c)
c1
- (d)
d3
Answer: Option D
Text Explanation :

Let P1, P2, P3, P4, P5 and P6 be the 6 pieces at positions A1, A3, B4, D7, H7 and H8 respectively.
1] If the queen is at position F8 it can attack P6 as it is in the same row and P3 as it in a diagonal position. However it cannot attack P2, which is in a diagonal position as P3 is placed between P2 and Q along the same diagonal. So a total of 2 pieces can be attacked if the queen is at position F8.
2] If the queen is at position A7 it can directly attack P4 as it is in the same row and P2 as it is in the same column. However it cannot attack P5 because P4 is in between the queen and P5. Similarly it cannot attack P1 because P2 is in between the Queen and P1. So a total of 2 pieces can be attacked by the queen if it is at position A7.
3] If the queen is at position C1, then it can only attack P1 which is in the same row and P2 which is along the same diagonal as the queen. So at positions C1, the queen can attack only 2 pieces.
4] If the queen is at position D3 then it can attack P2 along the same row, P4 along the same column and P5 along the same diagonal i.e., a total of 3 pieces. So out of the given options, the queen at position D3 can attack maximum number of pieces.
Hence, option (d).
Workspace:
If the other pieces are only at positions a1, a3, b4, d7, h7 and h8, then from how many positions the queen cannot attack any of the pieces?
- (a)
0
- (b)
3
- (c)
4
- (d)
6
Answer: Option C
Text Explanation :

All cells in rows 1, 3, 4, 7 and 8 and columns A, B, D and H will be eliminated as one of the ways the queen can the attack us from the same row or column. If we check for cell E2, F2, G2 and G5, queen will not be able to attack any of the 6 pieces. So, from a total of 4 positions, the queen cannot attack any of the 6 pieces.
Hence, option (d).
Workspace:
Suppose the queen is the only piece on the board and it is at position d5.
In how many positons can another piece be placed on the board such that it is safe from attack from the queen?
- (a)
32
- (b)
35
- (c)
36
- (d)
37
Answer: Option C
Text Explanation :

Let Q represent the position of the queen at cell D5. Now none of the pieces can be along column D or along row 5 i.e., a total of 8 + 8 – 1 = 15 cells (∵ D5 is common to column D and row 5 it is counted twice, hence we subtract 1) Now cells along the diagonal of D5 have to be eliminated since they can be directly attacked by the Queen from that cell. Therefore cells A8, B7, C6, E4, F3, G2, H1 and G8, F7, E6, C4, B3, A2 i.e., a total of 13 cells are not to be considered. So a total of 64 – 28 = 36 positions are considered safe from attack if the queen is at position D5
Hence, option (c).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report