LR - Arrangements - Previous Year CAT/MBA Questions
The best way to prepare for LR - Arrangements is by going through the previous year LR - Arrangements CAT questions. Here we bring you all previous year LR - Arrangements CAT questions along with detailed solutions.
Click here for previous year questions of other topics.
It would be best if you clear your concepts before you practice previous year LR - Arrangements CAT questions.
Answer the following questions based on the information given below:
The schematic diagram below shows 12 rectangular houses in a housing complex. House numbers are mentioned in the rectangles representing the houses. The houses are located in six columns – Column-A through Column-F, and two rows – Row-1 and Row-2. The houses are divided into two blocks - Block XX and Block YY. The diagram also shows two roads, one passing in front of the houses in Row-2 and another between the two blocks.

Some of the houses are occupied. The remaining ones are vacant and are the only ones available for sale.
The road adjacency value of a house is the number of its sides adjacent to a road. For example, the road adjacency values of C2, F2, and B1 are 2, 1, and 0, respectively. The neighbour count of a house is the number of sides of that house adjacent to occupied houses in the same block. For example, E1 and C1 can have the maximum possible neighbour counts of 3 and 2, respectively.
The base price of a vacant house is Rs. 10 lakhs if the house does not have a parking space, and Rs. 12 lakhs if it does. The quoted price (in lakhs of Rs.) of a vacant house is calculated as (base price) + 5 × (road adjacency value) + 3 × (neighbour count).
The following information is also known.
1. The maximum quoted price of a house in Block XX is Rs. 24 lakhs. The minimum quoted price of a house in block YY is Rs. 15 lakhs, and one such house is in Column-E.
2. Row-1 has two occupied houses, one in each block.
3. Both houses in Column-E are vacant. Each of Column-D and Column-F has at least one occupied house.
4. There is only one house with parking space in Block YY.
How many houses are vacant in Block XX?
Answer: 3
Text Explanation :
[Note: There might be discrepancy in one of the questions of this set. We will update the solution once the objections window closes and answers are updated by IIM Lucknow.]
Price of a house = (base price) + 5 × (road adjacency value) + 3 × (neighbor count)
Block XX:
Maximum price of a house in XX is 24
∴ 24 = (10 or 12) + 5 × (0 or 1 or 2) + 3 × (0 or 1 or 2 or 3)
This is only possible when:
base price = 10 lakhs, road adjacency = 1 and neighbor count = 3.
⇒ Only house B2 satisfies the given criteria i.e., road adjacency = 1 and neighbor count = 3.
∴ B2 is vacant and its price is 24 lakhs.
⇒ A2, B1 and C2 are occupied houses.
There is only one occupied house in Row 1 and block XX.
Since B1 is occupied, ⇒ A1 and C1 are vacant.
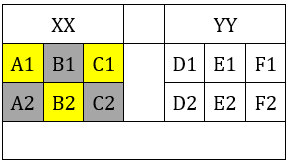
Block YY:
Both E1 and E2 are vacant and one of them costs 15 lakhs.
Let us focus on E1
For E1 neighbor count = 1 (exactly one of D1 or F1 is occupied)
For E1 road adjacency = 0
∴ Cost of E1 = (10 or 12) + 5 × 0 + 3 × 1 = 13 or 15 lakhs
Since 15 lakhs is the least cost of a house in block YY, E1 must cost 15 lakhs.
⇒ E1 is the only house in YY which has a parking space.
Given, Row-1 has two occupied houses, one in each block.
∴ Exactly one of D1 or F1 is occupied.
If F1 is vacant, let’s calculate its price.
It should not have parking space as only 1 house has parking space in block YY. Hence, it’s base price is 10 lakhs. Now even if F2 is occupied, F1’s price will be 10 + 0 + 3 = 13 lakhs.
This is not possible as least price for a house in YY is 15 lakhs.
∴ F1 should be occupied.
⇒ D1 is vacant.
Also, at least one house in column D is occupied, hence D2 must be occupied.
Now, F2 may be vacant or occupied, both cases are possible.

∴ 3 houses are vacant in block XX.
Hence, 3.
Workspace:
Which of the following houses is definitely occupied?
[Two options are correct in this question and both were accepted as correct answer by IIM Lucknow]
- (a)
D2
- (b)
F2
- (c)
B1
- (d)
A1
Answer: Option C
Text Explanation :
Consider the solution to first question of this set.
B1 and D2 are definitely occupied.
[Two options are correct in this question and both were accepted as correct answer by IIM Lucknow]
Hence, option (a) and (c).
Workspace:
Which of the following options best describes the number of vacant houses in Row-2?
- (a)
Exactly 3
- (b)
Exactly 2
- (c)
Either 3 or 4
- (d)
Either 2 or 3
Answer: Option D
Text Explanation :
Consider the solution to first question of this set.
In row 2, B2 and E2 are definitely vacant.
Out of D2 and F2, at least one is occupied, hence either 1 is vacant or 0 are vacant.
Case 1: One of D2 or F2 is vacant.
∴ We have B2, F2 and (D2 or F2), i.e., 3 houses vacant in row 2.
Case 2: None of D2 or F2 is vacant.
∴ We have B2 and F2, i.e., 2 houses vacant in row 2.
∴ In row 2, either only 2 houses are vacant or 3 houses are vacant.
Hence, option (d).
Workspace:
What is the maximum possible quoted price (in lakhs of Rs.) for a vacant house in Column-E?
Answer: 21
Text Explanation :
Consider the solution to first question of this set.
E1 costs 15 laks.
Let us calculate the maximum possible price of E2.
E2's base price is 10 lakh as it cannot have a parking space. (Only 1 house in YY i.e., E1 has a parking space.)
Road adjancecy for E2 = 1 and maximum neighbor count of E2 will be 2 (Both D2 and F2 are occupied and E1 is vacant)
∴ E2's price = 10 + 5 × 1 + 3 × 2 = 21 lakhs
Hence, 21.
Workspace:
Which house in Block YY has parking space?
- (a)
F2
- (b)
E2
- (c)
E1
- (d)
F1
Answer: Option C
Text Explanation :
Consider the solution to first question of this set.
Only 1 house in YY i.e., E1 has a parking space.
Hence, option (c).
Workspace:
Answer the following questions based on the information given below:
There are nine boxes arranged in a 3×3 array as shown in Tables 1 and 2. Each box contains three sacks. Each sack has a certain number of coins, between 1 and 9, both inclusive.
The average number of coins per sack in the boxes are all distinct integers. The total number of coins in each row is the same. The total number of coins in each column is also the same.

Table 1 gives information regarding the median of the numbers of coins in the three sacks in a box for some of the boxes. In Table 2 each box has a number which represents the number of sacks in that box having more than 5 coins. That number is followed by a * if the sacks in that box satisfy exactly one among the following three conditions, and it is followed by ** if two or more of these conditions are satisfied.
- The minimum among the numbers of coins in the three sacks in the box is 1.
- The median of the numbers of coins in the three sacks is 1.
- The maximum among the numbers of coins in the three sacks in the box is 9.
What is the total number of coins in all the boxes in the 3rd row?
- (a)
36
- (b)
30
- (c)
15
- (d)
45
Answer: Option D
Text Explanation :
Each box has three sacks. We will consider three values for each sacks representing the number of coins in each sack in ascending order.
Table 1: Medians of C1R2, C1R3, C2R1 and C3R1 are given. If numbers of coins in each sack is written in ascending order for all boxes, these medians will be the middle value.
Median for C2R1 is 9, hence the third value must be 9.

Table 2:
The number given represents the number of sacks having more than 5 coins. We can represent this information as follows:
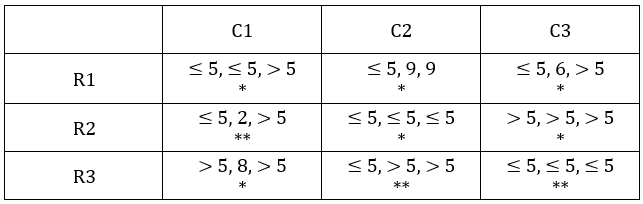
C2R1: The sum of coins so far is 9 + 9 = 18.
*Exactly one condition is satisfied i.e., highest number coins in a sack is 9.
The first sack should have coins less than 5 and the average should be an integer.
This is possible only when the first sack has 3 coins.
∴ Average number of coins/sack = (3 + 9 + 9)/3 = 7
C2R3: Median has to be greater than 5, hence condition 2 cannot be satisfied, hence conditions 1 and 3 have to be satisfied.
The first and third sacks have 1 and 9 coins respectively.
The second sack has more than 5 coins, such that the average is an integer. This is only possible when it has 8 coins.
∴ Average number of coins/sack = (1 + 8 + 9)/3 = 6
C2R2: If median is one, then first sack will also have 1 coin which would satisfy 2 of the given conditions, hence median cannot be 1.
Since all the values are less than or equal to 5, condition 3 cannot be satisfied.
Hence, the only condition that can be satisfied is the first condition that lowest number of coins is 1.
C1R2: **At least 2 conditions should be satisfied.
The median cannot be 1, hence the conditions to be satisfied are 1st and 3rd.
∴ Frist sack has 1 coin and third sack has 9 coins.
∴ Average number of coins/sack = (1 + 2 + 9)/3 = 4
C1R3: All sacks have more than 5 coins, hence condition 1 and 2 cannot be satisfied.
Hence, the only condition that can be satisfied is that the third sack has 9 coins.
Now, the two sacks have combined 8 + 9 = 17 coins.
The total should be a multiple of 3 (average is an integer), and the first sack has more than 5 coins. This is possible only when the third sack has 7 coins.
∴ Average number of coins/sack = (7 + 8 + 9)/3 = 8
C1R1: Since 2 conditions need to be satisfied and the average has to be an integer, this is possible when number of coins is 1, 1, 7 or 1, 5, 9
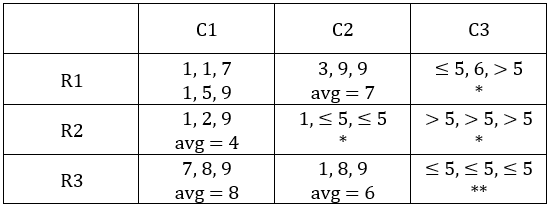
Case 1: C1R1 has 1, 5, 9 coins.
Total coins in C1 = 1 + 5 + 9 + 1 + 2 +9 + 7 + 8 + 9 = 51
Now C2 so far has = 3 + 9 + 9 + 1 + 1 + 8 + 9 = 40 coins
∴ C2 needs 51 – 40 = 11 more coins from two sacks in C2R2 block. This is not possible since these blocks have less than or equal to 5 coins each in them.
Hence, this case is rejected.
Case 2: C1R1 has 1, 1, 7 coins.
Total coins in C1 = 1 + 1 + 7 + 1 + 2 + 9 + 7 + 8 + 9 = 45
∴ Number of coins in the two sacks in C2R2 = 45 – 40 = 5 coins.
⇒ Number of coins in each column = 45.
C2R2: Since first condition is satisfied, no other condition should be satisfied. Also, the sum of coins in second and third sack is 5. This is possible when the number of coins in them is 2 and 3 respectively.

C3R3: All sacks have ≤ 5 coins hence condition 3 cannot be satisfied. Hence, the first two conditions should be satisfied.
⇒ The first and the second sacks have 1 coin each.
Since the average has to be an integer, the third sack can be 1 or 4 coins.
With 4 coins the average will become (1 + 1 + 4)/3 = 2 which cannot be the case since C2R1 already have average of 2 and all blocks have distinct averages.
∴ Third sack has 1 coin.
∴ Average number of coins/sack = (1 + 1 + 1)/3 = 1

The averages so far have been, 1, 2, 3, 4, 6, 7, and 8. So C3R1 and C3R2 will have average 6 or 9 in any order.
For average to be 9, all sacks must have exactly 9 coins. This is possible only for C3R2.
∴ Average for C3R2 is 9 and that for C3R1 is 5.
C3R1: will have a total of 5 × 3 = 15 coins.
Second sack has 6 coins, hence the other 2 sacks will have 15 – 6 = 9 coins.
Since exactly one condition has to be satisfied, this is possible when first sack has 1 coin and third sack has 8 coins.
Hence, we get the following final table.

Total coins in third row = 7 + 8 + 9 + 1 + 8 + 9 + 1 + 1 + 1 = 45
Hence, option (d)
Workspace:
How many boxes have at least one sack containing 9 coins?
- (a)
3
- (b)
8
- (c)
5
- (d)
4
Answer: Option C
Text Explanation :
Consider the solution to first questions of this set.

C1R2, C1R3, C2R1, C2R3 and C3R2 i.e., 5 blocks have at least one sack containing 9 coins.
Hence, option (c).
Workspace:
For how many boxes are the average and median of the numbers of coins contained in the three sacks in that box the same?
Answer: 4
Text Explanation :
Consider the solution to first questions of this set.

Average and median is same for C1R3, C2R2, C3R2 and C3R3 i.e., 4 blocks.
Hence, 4.
Workspace:
How many sacks have exactly one coin?
Answer: 9
Text Explanation :
Consider the solution to first questions of this set.

9 sacks have exactly 1 coin.
Hence, 9.
Workspace:
In how many boxes do all three sacks contain different numbers of coins?
Answer: 5
Text Explanation :
Consider the solution to first questions of this set.

C1R2, C1R3, C2R2, C2R3 and C3R1 i.e., 5 blocks all sacks containing different number of coins.
Hence, 5.
Workspace:
Answer the next 5 questions based on the information given below:
There are only four neighbourhoods in a city - Levmisto, Tyhrmisto, Pesmisto and Kitmisto. During the onset of a pandemic, the number of new cases of a disease in each of these neighbourhoods was recorded over a period of five days. On each day, the number of new cases recorded in any of the neighbourhoods was either 0, 1, 2 or 3.
The following facts are also known:
1. There was at least one new case in every neighbourhood on Day 1.
2. On each of the five days, there were more new cases in Kitmisto than in Pesmisto.
3. The number of new cases in the city in a day kept increasing during the five-day period. The number of new cases on Day 3 was exactly one more than that on Day 2.
4. The maximum number of new cases in a day in Pesmisto was 2, and this happened only once during the five-day period.
5. Kitmisto is the only place to have 3 new cases on Day 2.
6. The total numbers of new cases in Levmisto, Tyhrmisto, Pesmisto and Kitmisto over the five-day period were 12, 12, 5 and 14 respectively.
What BEST can be concluded about the total number of new cases in the city on Day 2?
- (a)
Exactly 7
- (b)
Either 7 or 8
- (c)
Either 6 or 7
- (d)
Exactly 8
Answer: Option D
Text Explanation :
We can make the following table:
1. There was at least one new case in every neighborhood on Day 1.
2. On each of the five days, there were more new cases in Kitmisto than in Pesmisto.
3. The number of new cases in the city in a day kept increasing during the five-day period. The number of new cases on Day 3 was exactly one more than that on Day 2.
5. Kitmisto is the only place to have 3 new cases on Day 2.
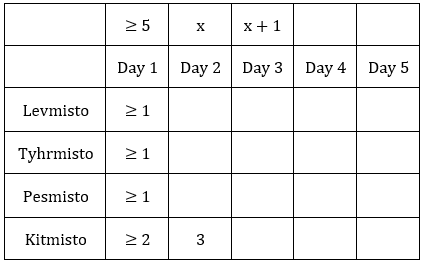
From (6): The total numbers of new cases in Levmisto, Tyhrmisto, Pesmisto and Kitmisto over the five-day period were 12, 12, 5 and 14 respectively.
Total cases during the 5 days = 12 + 12 + 5 + 14 = 43
On day 5, neighborhoods L, T and K can have maximum 3 cases each, while P can have maximum 2 cases. Hence, maximum possible total cases on day 5 = 3 + 2 + 3 + 3 = 11.
⇒ Maximum possible cases on day 4 = 10.
∴ Maximum possible cases on day 4 + day 5 = 10 + 11 = 21.
Since on day 1 there will be at least 5 cases in the city and every day total cases increase, hence on day 2 total cases must be 6 or more.
Case 1: Total cases on Day 2 = 6
⇒ Total cases on Day 3 = 7
⇒ Total cases on Day 1 = 5
∴ Total cases on day 4 + day 5 = 43 – (5 + 6 + 7) = 25
This is not possible as maximum cases possible on day 4 + day 5 is 21.
Case 2: Total cases on Day 2 = 7
⇒ Total cases on Day 3 = 8
⇒ Total cases on Day 1 = 5 or 6
∴ Total cases on day 4 + day 5 = 43 – (5/6 + 7 + 8) = 23 or 22
This is not possible as maximum cases possible on day 4 + day 5 is 21.
Case 3: Total cases on Day 2 = 8
⇒ Total cases on Day 3 = 9
Since total cases on day 4 cannot be more than 10, hence total cases on day 4 = 10.
Since total cases on day 5 cannot be more than 11, hence total cases on day 5 = 11.
⇒ Total cases on Day 1 = 43 – (8 + 9 + 10 + 11) = 5
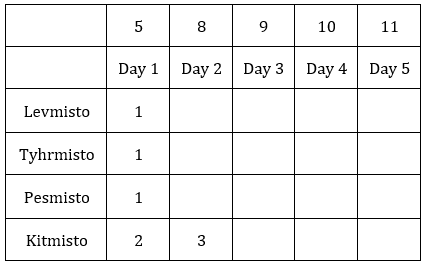
Only possibility for total cases of 11 on day 5 is: L – 3, T – 3, P – 2, K – 3.
Only possibility for total cases of 11 on day 5 is: L – 3, T – 3, P – 1, K – 3.
[Note: There is only 1 day when Pesmisto had 2 cases. On remaining days P will have less than 2 cases.]
Total cases in Kitmisto is 14. This is possible when there are 3 cases on 4 days each and 2 cases on the remaining 5th day.
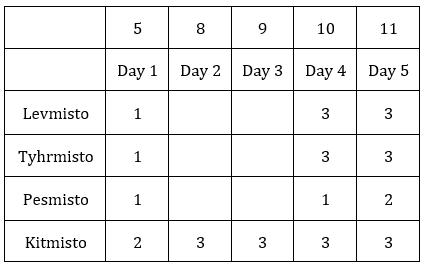
Levmisto and Tyhrmisto have total 12 cases.
Total cases on day 2 + day 3 for these two neighborhoods = 12 – (1 + 3 + 3) = 5
5 cases in 2 days are possible when there are 2 and 3 cases in these 2 days.
On day 2 only Kitmisto had 3 cases, hence we can fill the table accordingly.
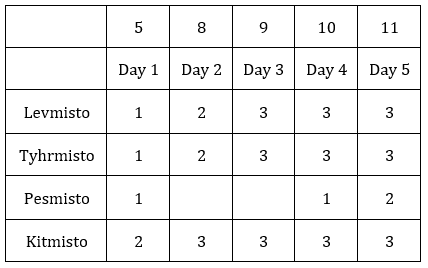
Now the remaining 2 slots can be filled.

∴ The total number of new cases in the city on Day 2 = 8
Hence, option (d).
Workspace:
What BEST can be concluded about the number of new cases in Levmisto on Day 3?
- (a)
Either 2 or 3
- (b)
Exactly 3
- (c)
Either 0 or 1
- (d)
Exactly 2
Answer: Option B
Text Explanation :
Consider the solution to first question of this set.
∴ The number of new cases in Levmisto on Day 3 = 3.
Hence, option (b).
Workspace:
On which day(s) did Pesmisto not have any new case?
- (a)
Both Day 2 and Day 3
- (b)
Only Day 2
- (c)
Only Day 3
- (d)
Both Day 2 and Day 4
Answer: Option C
Text Explanation :
Consider the solution to first question of this set.
∴ The number of new cases in Levmisto on Day 3 = 3.
Hence, option (b).
Workspace:
Which of the two statements below is/are necessarily false?
Statement A: There were 2 new cases in Tyhrmisto on Day 3.
Statement B: There were no new cases in Pesmisto on Day 2.
- (a)
Statement B only
- (b)
Statement A only
- (c)
Both Statement A and Statement B
- (d)
Neither Statement A nor Statement B
Answer: Option C
Text Explanation :
Consider the solution to first question of this set.
Both Statement A and Statement B are false.
Hence, option (c).
Workspace:
On how many days did Levmisto and Tyhrmisto have the same number of new cases?
- (a)
5
- (b)
4
- (c)
3
- (d)
2
Answer: Option A
Text Explanation :
Consider the solution to first question of this set.
Levmisto and Tyhrmisto have the same number of new cases on all 5 days.
Hence, option (c).
Workspace:
Answer the following question based on the information given below.
A supermarket has to place 12 items (coded A to L) in shelves numbered 1 to 16. Five of these items are types of biscuits, three are types of candies and the rest are types of savouries. Only one item can be kept in a shelf. Items are to be placed such that all items of same type are clustered together with no empty shelf between items of the same type and at least one empty shelf between two different types of items. At most two empty shelves can have consecutive numbers.
The following additional facts are known.
- A and B are to be placed in consecutively numbered shelves in increasing order.
- I and J are to be placed in consecutively numbered shelves both higher numbered than the shelves in which A and B are kept.
- D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies.
- K is to be placed in shelf number 16.
- L and J are items of the same type, while H is an item of a different type.
- C is a candy and is to be placed in a shelf preceded by two empty shelves.
- L is to be placed in a shelf preceded by exactly one empty shelf.
In how many different ways can the items be arranged on the shelves?
- (a)
1
- (b)
8
- (c)
2
- (d)
4
Answer: Option B
Text Explanation :
There are 5 types of biscuits, 3 types of candies and 4 types of savouries. Among 16 shelves, there are 4 empty shelves.
It is given that all items of same type are clustered together with no empty shelf between items of the same type.
From (3) and (4), it can be concluded that D, E, F and K are savouries.
From (2) and (5), L, I and J are of one type and H is the other type. Therefore from (6), as C is a candy, L, I J must be types of biscuits and H is a type of candy. Now using (1), we can conclude that A and B are of one type but not candies as there are only 3 types of candies.
Therefore,
Biscuits: A, B, I, J, L Candies: C, H, G Savouries: D, E, F, K
From (3), (4), (6) and (7), there shelf number 12 must be an empty shelf. Also, D, E, F and K are placed in shelves numbered 13, 14, 15 and 16 respectively.
Now from (1), (2) and (7), the sequence (from left to right) in which biscuits are kept is:
(Empty shelf), L, A, B, (I/J), (J/I).
From (6), the candies must be in the following order: (Empty shelf), (Empty shelf), C, (H/G), (G/H)
Thus, we have

In each case, J and I can be arranged in 2 ways and G and H can be arranged among them in 2 ways. Thus, 2 × 2 = 4 ways.
Total number of ways the items can be arranged on the shelves = 4 + 4 = 8
Hence, option (b).
Workspace:
Which of the following items is not a type of biscuit?
- (a)
A
- (b)
B
- (c)
L
- (d)
G
Answer: Option D
Text Explanation :
Consdier the solution to first question of this set.
G is not a type of biscuit. It is a candy.
Hence, option (d).
Workspace:
Which of the following can represent the numbers of the empty shelves in a possible arrangement?
- (a)
1,2,8,12
- (b)
1,7,11,12
- (c)
1,5,6,12
- (d)
1,2,6,12
Answer: Option D
Text Explanation :
Consdier the solution to first question of this set.
In the second case we have shelf 1, 2, 6 and 12 empty.
Hence, option (d).
Workspace:
Which of the following statements is necessarily true?
- (a)
There are at least four shelves between items B and C.
- (b)
There are two empty shelves between the biscuits and the candies.
- (c)
All biscuits are kept before candies.
- (d)
All candies are kept before biscuits.
Answer: Option A
Text Explanation :
Consdier the solution to first question of this set.
Considering case (i): There are 4 shelves between B and C.
Considering case (ii): There are 5 shelves between B and C.
Hence, there are at least 4 shelves between B and C.
Hence, option (a).
Workspace:
Answer the following question based on the information given below.
In a square layout of size 5m × 5m, 25 equal-sized square platforms of different heights are built.
The heights (in metres) of individual platforms are as shown below:
6 1 2 4 3
9 5 3 2 8
7 8 4 6 5
3 9 5 1 2
1 7 6 3 9
Individuals (all of same height) are seated on these platforms. We say an individual A can reach an individual B if all the three following conditions are met:
(i) A and B are in the same row or column
(ii) A is at a lower height than B
(iii) If there is / are any individual(s) between A and B, such individual(s) must be at a height lower than that of A.
Thus in the table given above, consider the individual seated at height 8 on 3rd row and 2nd column. He can be reached by four individuals. He can be reached by the individual on his left at height 7, by the two individuals on his right at heights of 4 and 6 and by the individual above at height 5.
Rows in the layout are numbered from top to bottom and columns are numbered from left to right.
How many individuals in this layout can be reached by just one individual?
- (a)
3
- (b)
5
- (c)
7
- (d)
8
Answer: Option C
Text Explanation :
Let us check how many people in the grid can reach individuals. Let us do this by moving row wise
Row 1
6 – Can be reached by 1, 2 and 4 in the same row i.e., a total of 3 people
1 – Cannot be reached by anyone
2 – Can be reached by only 1 in the same row on the left
4 – Can be reached by 3 people i.e., 2 and 3 in the same row and 2 in the column below
3 – Cannot be reached by anyone
In a similar way we proceed for the other rows
Row 2
9 – Can be reached by 6, 5, 8 and 7 i.e., of total of 4 people
5 – Can be reached by 1 and 3 i.e., a total of 2 people
3 – Can be reach by 2 and 2 i.e., a total of 2 people
2 – Cannot be reached by anyone
8 – Can be reached by 5 people i.e., 2, 3 and 5 in the same row, 3 in the column above above and 5 in the column below.
Row 3
7 – Can be reached by only 3 in the row below
8 – Can be reached 5, 7, 4, and 6 i.e., total of 4 people
4 – Can be reached by only 3 in the above row
6 – Can be reached only by 4 and 5 in the same row and 4, 2, 1 and 3 in the same column i.e., a total of 6 people
5 – Can only be reached by 2 in the same row below
Row 4
3 – Can only be reached by 1 in the row below
9 – Can be reached by 3 and 5 in the same row and 7 & 8 in the row below and above i.e., a total of 4 people
5 – Can be reached by 1 & 2 in the same row and 4 in the row above
1 – Cannot be reached by anyone
2 – Can be reached only by 1 in the same row
Row 5
1 – Cannot be reached by anyone
7 – Can be reached by 1 and 6 in the same row i.e., a total of 2 people
6 – Can be reached by 5 in the row above and 3 in the same row. i.e., a total of 2 people
3 – Can be reached only by 1 in the row above
9 – Can be reached by 3, 6 and 7 in the same row and 2, 5 and 8 in the rows above i.e., a total of 6 people
Looking at the table we can see the person having height 2 m in the 1st row, people having height 7 m, 4 m and 5 m in the 3rd row, people having height 3 m and 2 m in the 4th row and the person having height 3 m in the 5th row i.e., a total of 7 people can be reached by only one person.
Hence, option (c).
Workspace:
Which of the following is true for any individual at a platform of height 1 m in this layout?
- (a)
They can be reached by all the individuals in their own row and column.
- (b)
They can be reached by at least 4 individuals.
- (c)
They can be reached by at least one individual.
- (d)
They cannot be reached by anyone.
Answer: Option D
Text Explanation :
Let us check how many people in the grid can reach individuals. Let us do this by moving row wise
Row 1
6 – Can be reached by 1, 2 and 4 in the same row i.e., a total of 3 people
1 – Cannot be reached by anyone
2 – Can be reached by only 1 in the same row on the left
4 – Can be reached by 3 people i.e., 2 and 3 in the same row and 2 in the column below
3 – Cannot be reached by anyone
In a similar way we proceed for the other rows
Row 2
9 – Can be reached by 6, 5, 8 and 7 i.e., of total of 4 people
5 – Can be reached by 1 and 3 i.e., a total of 2 people
3 – Can be reach by 2 and 2 i.e., a total of 2 people
2 – Cannot be reached by anyone
8 – Can be reached by 5 people i.e., 2, 3 and 5 in the same row, 3 in the column above above and 5 in the column below.
Row 3
7 – Can be reached by only 3 in the row below
8 – Can be reached 5, 7, 4, and 6 i.e., total of 4 people
4 – Can be reached by only 3 in the above row
6 – Can be reached only by 4 and 5 in the same row and 4, 2, 1 and 3 in the same column i.e., a total of 6 people
5 – Can only be reached by 2 in the same row below
Row 4
3 – Can only be reached by 1 in the row below
9 – Can be reached by 3 and 5 in the same row and 7 & 8 in the row below and above i.e., a total of 4 people
5 – Can be reached by 1 & 2 in the same row and 4 in the row above
1 – Cannot be reached by anyone
2 – Can be reached only by 1 in the same row
Row 5
1 – Cannot be reached by anyone
7 – Can be reached by 1 and 6 in the same row i.e., a total of 2 people
6 – Can be reached by 5 in the row above and 3 in the same row. i.e., a total of 2 people
3 – Can be reached only by 1 in the row above
9 – Can be reached by 3, 6 and 7 in the same row and 2, 5 and 8 in the rows above i.e., a total of 6 people
Looking at the table we can see the person having height 2 m in the 1st row, people having height 7 m, 4 m and 5 m in the 3rd row, people having height 3 m and 2 m in the 4th row and the person having height 3 m in the 5th row i.e., a total of 7 people can be reached by only one person.
A person having a height of 1 m cannot be reached by anyone.
Hence, option (d).
Workspace:
We can find two individuals who cannot be reached anyone in
- (a)
the last row.
- (b)
the fourth row.
- (c)
the fourth column.
- (d)
the middle column.
Answer: Option C
Text Explanation :
Let us check how many people in the grid can reach individuals. Let us do this by moving row wise
Row 1
6 – Can be reached by 1, 2 and 4 in the same row i.e., a total of 3 people
1 – Cannot be reached by anyone
2 – Can be reached by only 1 in the same row on the left
4 – Can be reached by 3 people i.e., 2 and 3 in the same row and 2 in the column below
3 – Cannot be reached by anyone
In a similar way we proceed for the other rows
Row 2
9 – Can be reached by 6, 5, 8 and 7 i.e., of total of 4 people
5 – Can be reached by 1 and 3 i.e., a total of 2 people
3 – Can be reach by 2 and 2 i.e., a total of 2 people
2 – Cannot be reached by anyone
8 – Can be reached by 5 people i.e., 2, 3 and 5 in the same row, 3 in the column above above and 5 in the column below.
Row 3
7 – Can be reached by only 3 in the row below
8 – Can be reached 5, 7, 4, and 6 i.e., total of 4 people
4 – Can be reached by only 3 in the above row
6 – Can be reached only by 4 and 5 in the same row and 4, 2, 1 and 3 in the same column i.e., a total of 6 people
5 – Can only be reached by 2 in the same row below
Row 4
3 – Can only be reached by 1 in the row below
9 – Can be reached by 3 and 5 in the same row and 7 & 8 in the row below and above i.e., a total of 4 people
5 – Can be reached by 1 & 2 in the same row and 4 in the row above
1 – Cannot be reached by anyone
2 – Can be reached only by 1 in the same row
Row 5
1 – Cannot be reached by anyone
7 – Can be reached by 1 and 6 in the same row i.e., a total of 2 people
6 – Can be reached by 5 in the row above and 3 in the same row. i.e., a total of 2 people
3 – Can be reached only by 1 in the row above
9 – Can be reached by 3, 6 and 7 in the same row and 2, 5 and 8 in the rows above i.e., a total of 6 people
Looking at the table we can see the person having height 2 m in the 1st row, people having height 7 m, 4 m and 5 m in the 3rd row, people having height 3 m and 2 m in the 4th row and the person having height 3 m in the 5th row i.e., a total of 7 people can be reached by only one person.
In the last row there is only one individual with height 3 m who cannot be reached.
So option [1] is ruled out. Similarly, in the 4th row there is only one person with height 1 m who cannot be reached by anyone. So option [2] is also incorrect.
In the 4th column, there are 2 people, one with 2 m height and one with 1 m height who cannot be reached by anyone.
So option [3] is correct. In the middle column there is no one who cannot be reached by anyone. So option [4] is also incorrect.
Hence, option (c).
Workspace:
Which of the following statements is true about this layout?
- (a)
Each row has an individual who can be reached by 5 or more individuals.
- (b)
Each row has an individual who cannot be reached by anyone.
- (c)
Each row has at least two individuals who can be reached by an equal number of individuals.
- (d)
All individuals at the height of 9 m can be reached by at least 5 individuals.
Answer: Option C
Text Explanation :
Let us check how many people in the grid can reach individuals. Let us do this by moving row wise
Row 1
6 – Can be reached by 1, 2 and 4 in the same row i.e., a total of 3 people
1 – Cannot be reached by anyone
2 – Can be reached by only 1 in the same row on the left
4 – Can be reached by 3 people i.e., 2 and 3 in the same row and 2 in the column below
3 – Cannot be reached by anyone
In a similar way we proceed for the other rows
Row 2
9 – Can be reached by 6, 5, 8 and 7 i.e., of total of 4 people
5 – Can be reached by 1 and 3 i.e., a total of 2 people
3 – Can be reach by 2 and 2 i.e., a total of 2 people
2 – Cannot be reached by anyone
8 – Can be reached by 5 people i.e., 2, 3 and 5 in the same row, 3 in the column above above and 5 in the column below.
Row 3
7 – Can be reached by only 3 in the row below
8 – Can be reached 5, 7, 4, and 6 i.e., total of 4 people
4 – Can be reached by only 3 in the above row
6 – Can be reached only by 4 and 5 in the same row and 4, 2, 1 and 3 in the same column i.e., a total of 6 people
5 – Can only be reached by 2 in the same row below
Row 4
3 – Can only be reached by 1 in the row below
9 – Can be reached by 3 and 5 in the same row and 7 & 8 in the row below and above i.e., a total of 4 people
5 – Can be reached by 1 & 2 in the same row and 4 in the row above
1 – Cannot be reached by anyone
2 – Can be reached only by 1 in the same row
Row 5
1 – Cannot be reached by anyone
7 – Can be reached by 1 and 6 in the same row i.e., a total of 2 people
6 – Can be reached by 5 in the row above and 3 in the same row. i.e., a total of 2 people
3 – Can be reached only by 1 in the row above
9 – Can be reached by 3, 6 and 7 in the same row and 2, 5 and 8 in the rows above i.e., a total of 6 people
Looking at the table we can see the person having height 2 m in the 1st row, people having height 7 m, 4 m and 5 m in the 3rd row, people having height 3 m and 2 m in the 4th row and the person having height 3 m in the 5th row i.e., a total of 7 people can be reached by only one person.
In row 1, the maximum number of people who can reach a particular individual is 3, which is for the person with height 6 m and for the person with height 4 m. So statement (1) is false.
Row 3 does not have any individual who cannot be reached by anyone. Hence statement [2] is false.
In row 1, person with height 6 m and person with height 4 m can each be reached by 3 people. In row 2 people with height 5 m and 3 m can each be reached by 2 people.
In Row 3, people with height 7 m and 3 m can be reached by only 1 person. In Row 4, people with height 3 m and 2 m can be reached by only 1 person. In Row 5, people with height 7 m and 6 m can be reached by 2 people each. So in each row we have 2 individuals who can be reached by an equal number of individuals.
So statement 3 is true. Individual with height 9 m in row 2 can be reached by 4 people.
Hence, option (c).
Workspace:
Answer the following question based on the information given below.
A tea taster was assigned to rate teas from six different locations – Munnar, Wayanand, Ooty, Darjeeling, Assam and Himachal. These teas were placed in six cups, numbered 1 to 6, not necessarily in the same order. The tea taster was asked to rate these teas on the strength of their flavour on a scale of 1 to 10. He gave a unique integer rating to each tea. Some other information is given below:
- Cup 6 contained tea from Himachal.
- Tea from Ooty got the highest rating, but it was not in Cup 3.
- The rating of tea in Cup 3 was double the rating of the tea in Cup 5.
- Only two cups got ratings in even numbers.
- Cup 2 got the minimum rating and this rating was an even number.
- Tea in Cup 3 got a higher rating than that in Cup 1.
- The rating of tea from Wayanad was more than the rating of tea from Munnar, but less than that from Assam.
What was the second highest rating given?
Answer: 7
Text Explanation :
Following condition (1) and (2) we can form the table as below

Now rating of Tea in cup 3 is twice the rating of tea in cup 5. So the rating of tea in cup 3 will be an even number. Now following condition. (4) and (5) we know that cup 2 and cup 3 are the only cups that have an even numbered rating. This means that the rating of tea in cup 1, 4, 5 and 6 will be an odd number. Now since the rating of cup 3 is twice the rating of cup 5 which has an odd numbered rating, rating of cup 5 will be 3. The reason for this is that the since the rating of cup 2 is the least and an even number, the rating of cup 5 has to be higher than that of cup 2 (which will be atleast 2) and hence it’s rating cannot be 1. Further, since only the rating of cup 2 and cup 3 are even numbers and neither of them contains the highest rated tea, so then rating of Tea in Ooty (which is not in cup 3) will be less than 10. So this means the only possibility for rating of tea in cup 3 has to be 6, as that is the only even number which is twice that of an odd number. This further implies that the rating of tea in cup 5 is 3. This also means that rating of Tea in cup 2 is 2. We know need to find the ratings of tea in cups 1, 4 and 6. Further, as all these cups will be 5, 7 and 9 (not essentially in that order). Since the rating of tea in cup 3 (which is 6) is higher than the rating of tea in cup 1, the rating of tea in cup 1 has to be 5. Further, tea from Ooty is placed in cup 4 and since the tea from Ooty has the highest rating it’s rating will be 9. This would mean that the rating of tea from Himachal in cup 6 will be 7. The only other information we have is that Tea from Assam has a better rating than Tea from Wayanand which in turn is better than Tea from Munnar.

We have no other information about the location of tea in cups 1, 2, 3 and 5. So using the table above let us answer the questions.
As can be seen from the table, 2nd highest rating given was 7.
Answer: 7
Workspace:
What was the number of the cup that contained tea from Ooty?
Answer: 4
Text Explanation :
Following condition (1) and (2) we can form the table as below

Now rating of Tea in cup 3 is twice the rating of tea in cup 5. So the rating of tea in cup 3 will be an even number. Now following condition. (4) and (5) we know that cup 2 and cup 3 are the only cups that have an even numbered rating. This means that the rating of tea in cup 1, 4, 5 and 6 will be an odd number. Now since the rating of cup 3 is twice the rating of cup 5 which has an odd numbered rating, rating of cup 5 will be 3. The reason for this is that the since the rating of cup 2 is the least and an even number, the rating of cup 5 has to be higher than that of cup 2 (which will be atleast 2) and hence it’s rating cannot be 1. Further, since only the rating of cup 2 and cup 3 are even numbers and neither of them contains the highest rated tea, so then rating of Tea in Ooty (which is not in cup 3) will be less than 10. So this means the only possibility for rating of tea in cup 3 has to be 6, as that is the only even number which is twice that of an odd number. This further implies that the rating of tea in cup 5 is 3. This also means that rating of Tea in cup 2 is 2. We know need to find the ratings of tea in cups 1, 4 and 6. Further, as all these cups will be 5, 7 and 9 (not essentially in that order). Since the rating of tea in cup 3 (which is 6) is higher than the rating of tea in cup 1, the rating of tea in cup 1 has to be 5. Further, tea from Ooty is placed in cup 4 and since the tea from Ooty has the highest rating it’s rating will be 9. This would mean that the rating of tea from Himachal in cup 6 will be 7. The only other information we have is that Tea from Assam has a better rating than Tea from Wayanand which in turn is better than Tea from Munnar.

We have no other information about the location of tea in cups 1, 2, 3 and 5. So using the table above let us answer the questions.
The number of the cup that contained the tea from Ooty is 4.
Answer: 4
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report