CUET-PG 2023 General MBA questions and solutions

1. CUET-PG 2023 General MBA | Ratio, Proportion and Partnership

A started a business with Rs. 25,000 and is joined afterwards by B with Rs. 40,000. After how many months did B join if the profits at the end of the year are divided equally?

A.
3
B.
4
C.
4.5
D.
5

Answer: Option C

Explanation :

A invested for 1 year i.e., 12 months.
Let the time invested by B is x months.

We know that ratio of profit = ratio of (investment × time)

$\frac{Profit of A}{Profit of B}$ = $\frac{I_{A} \times T_{A}}{I_{B} \times T_{B}}$

⇒ $\frac{1}{1}$ = $\frac{25000 \times 12}{40000 \times x}$

⇒ 40000x = 25000 × 12

⇒ 8x = 5 × 12

⇒ x = 60/8 = 7.5

∴ B invested after 12 - 7.5 = 4.5 months.

Hence, option (c).

2. CUET-PG 2023 General MBA | Ratio, Proportion and Partnership

Three partners P, Q, R start a business. Twice of P's capital is equal to thrice of Q's capital and Q's capital is four times R's capital. Out of a total profit of Rs. 27,500 at the end of the year, Q's share is:

A.
Rs. 8,000
B.
Rs. 10,000
C.
Rs. 12,000
D.
Rs. 14,000

3. CUET-PG 2023 General MBA | Simple and Compound Interest

An amout of Rs. 10,000 becomes Rs. 14,641 in 2 years if the interest is compounded half-yearly. What is the rate of compound interest per annum?

A.
10%
B.
15%
C.
20%
D.
25%

Answer: Option C

Explanation :

Let the interest rate be r% p.a.

If compounding is done n times in a year, the amount due after t years can be calclated as $P \times {(1 + \frac{r / n}{100})}^{t \times n}$

Here, compounding in done 2 times in a year, hence n = 2.

⇒ 14641 = $10000 \times {(1 + \frac{r / 2}{100})}^{2 \times 2}$

⇒ 14641 = $10000 \times {(1 + \frac{r / 2}{100})}^{4}$

⇒ 11⁴ = $10^{4} \times {(1 + \frac{r / 2}{100})}^{4}$

⇒ 11 = $10 \times (1 + \frac{r / 2}{100})$

⇒ $(1 + \frac{r / 2}{100})$ = 1.1

⇒ r/2 = 10

⇒ r = 20%

Hence, option (c).

4. CUET-PG 2023 General MBA | Percentage, Profit & Loss

A man bought goods worth Rs. 10,000 and sold half of them at a gain of 10%. At what gain percent must he sell the remainder so as to get a gain of 25% on the whole?

A.
10%
B.
15%
C.
25%
D.
40%

5. CUET-PG 2023 General MBA | Percentage, Profit & Loss

If a shopkeeper sells 1/3 of his goods at a profit of 14%, 3/5 of the goods at a profit of 17.5% and the remaining at a profit of 20%, then his profit on the whole is equal to:

A.
15%
B.
16.5%
C.
20%
D.
25%

6. CUET-PG 2023 General MBA | Linear & Quadratic Equations

Aman got 76% marks and Neha got 480 marks in a test. The maximum marks of the test is equal to the marks obtained by Aman and Neha together. How many marks did Aman score in the test?

A.
1300
B.
1420
C.
1500
D.
1520

7. CUET-PG 2023 General MBA | Percentage, Profit & Loss

If the price of rice falls by 2½ %, a person can buy 9 kg more of rice for Rs. 1,260 than before. If the price had risen 12½ %, how much rice would he have bought for the same sum?

A.
310 kg
B.
312 kg
C.
315 kg
D.
320 kg

8. CUET-PG 2023 General MBA | Ratio, Proportion and Partnership

Rs. 1,820 are divided among A, B and C. The share of A is 2/5 of the combined share of B and C. Then A gets how much amount?

A.
Rs. 420
B.
Rs. 480
C.
Rs. 500
D.
Rs. 520

9. CUET-PG 2023 General MBA | Ratio, Proportion and Partnership

The ages of P and Q are presently in the ratio of 5 : 6 respectively. After six years, this ratio will become 6 : 7 respectively. What was Q's age 10 years ago?

A.
26 years
B.
31 years
C.
33 years
D.
35 years

Answer: Option A

Explanation :

Present ages of P and Q are in the ratio 5 : 6.
⇒ Let present age of P be 5x and that of Q be 6x.

Their ages after six years will be 5x + 6 and 6x + 6 respectively.
Now, ratio of these ages is 6 : 7.

⇒ $\frac{5 x + 6}{6 x + 6}$ = $\frac{6}{7}$

⇒ 7 × (5x + 6) = 6 × (6x + 6)
⇒ 35x + 42 = 36x + 36
⇒ x = 6

∴ Q;s present age = 6x = 36 years.

⇒ Q's age 10 years ago = 36 - 10 = 26 years.

Hence, option (a).

10. CUET-PG 2023 General MBA | Time and Work

Three pipes P, Q and R can fill a tank in 6 hours. After working at it together for 2 hours, R is closed and P and Q can fill the remaining part in 7 hours. The number of hours taken by R alone to fill the tank is:

A.
10
B.
12
C.
14
D.
16

Answer: Option C

Explanation :

P, Q and R together can complete the whole work in 6 hours.
∴ In 2 hours they would have completed 2/6 = 1/3^rd of the tank

The remaining 2/3^rd of the tank is filled by P and Q in 7 hours.
If P and Q can fill 2/3^rd tank in 7 hours, they can fill the whole tank in 7 × 3/2 = 10.5 hours.
Combined efficiency of P and Q = $\frac{1}{10.5}$

P, Q and R together can complete the whole work in 6 hours.
⇒ $\frac{1}{6} = \frac{1}{P} + \frac{1}{Q} + \frac{1}{R}$

Now, $\frac{1}{P} + \frac{1}{Q}$ is combined efficiency of P and Q which will be $\frac{1}{10.5}$

⇒ $\frac{1}{6} = \frac{1}{10.5} + \frac{1}{R}$

⇒ $\frac{1}{R} = \frac{1}{6} - \frac{1}{10.5}$

⇒ R = 42/3 = 14 hours

Hence, option (c).

11. CUET-PG 2023 General MBA | Time and Work

P takes twice as much time as Q or thrice as much time as R to finish a piece of work. Working together, they can finish the work in 5 days. Q can do the work alone in

A.
10 days
B.
13 days
C.
15 days
D.
18 days

Answer: Option C

Explanation :

Let the time taken by P alone be 6x days.
∴ Time taken by Q alone will be 3x days and that by R will be 2x days.

Working together the three of them can finish the work in 5 days.

⇒ $\frac{1}{5} = \frac{1}{P} + \frac{1}{Q} + \frac{1}{R}$

⇒ $\frac{1}{5} = \frac{1}{6 x} + \frac{1}{3 x} + \frac{1}{2 x}$

⇒ $\frac{1}{5} = \frac{1 + 2 + 3}{6 x}$

⇒ $\frac{1}{5} = \frac{1}{x}$

⇒ x = 5

∴ Q alone can complete the work in 3x = 15 days.

Hence, option (c).

12. CUET-PG 2023 General MBA | Time, Speed and Distance

Rohan takes 2 hours more than Soham to walk 50 km,but if Rohan doubles his speed, then he can make it in 1 hour less than Soham. How much time does Soham require for walking 50 km?

A.
4 hrs
B.
6 hrs
C.
8 hrs
D.
10 hrs

Answer: Option A

Explanation :

Let time taken by Soham and Rohan to walk 50 kms be t and t + 2 hours respectively.

⇒ Soham's speed = 50/t
⇒ Rohan's speed = 50/(t + 2)

With double speed Rohan takes 1 hour less than Soham to walk 50 kms.

⇒ $\frac{50}{2 \times (\frac{50}{t + 2})}$ = t - 1

⇒ 50 = $2 \times (\frac{50}{t + 2}) \times (t - 1)$

⇒ $\frac{1}{2}$ = $(\frac{t - 1}{t + 2})$

⇒ t + 2 = 2(t - 1)

⇒ t = 4 hours.

Hence, option (a).

13. CUET-PG 2023 General MBA | Time, Speed and Distance

Two trains of equal length are running on parallel tracks in the same direction at 40 km/h and 30km/h. The faster train passes the slower train in 54 seconds. The length of each train is:

A.
50 m
B.
60 m
C.
70 m
D.
75 m

Answer: Option D

Explanation :

When running in same direction, time taken for two trains to cross each other = $\frac{L_{1} + L_{2}}{f - s}$

L1 and L2 are the lengths of the two trains while f and s are the speeds of faster and slower trains respectively.

Let the length of the two trains be L (same length).

⇒ 54 = $\frac{L + L}{(40 - 30) \times \frac{5}{18}}$

⇒ 54 × 50/18 = 2L

⇒ 2L = 150

⇒ L = 75 meters

Hence, option (d).

14. CUET-PG 2023 General MBA | Average, Mixture & Alligation

The milk and water in two vessels P and Q are in the ratio 5 : 2 and 2 : 3 respectively. In what ratio, the liquids in both the vessels be mixed to obtain a new mixture in vessel R containing half milk and half water?

A.
3 : 14
B.
7 :15
C.
3:10
D.
1 : 15

15. CUET-PG 2023 General MBA | Average, Mixture & Alligation

How many liters of water should be added to a 30 liters mixture of milk and water in the ratio of 7 : 3, such that the resultant mixture has 60% milk in it?

A.
6
B.
5
C.
4
D.
3
E.
30 liter of mixture has milk and water in the ratio 7 : 3
∴ Amount of milk in the mixture = 7/10 × 30 = 21 liters
∴ Amount of water in the mixture = 3/10 × 30 = 9 liters

Let x liters of water is added to this mixture.

The resultant solution has 21 liters of milk and 9 + x liters of water.

Milk is 60% of the solution
⇒ 21 = 0.6 × (21 + 9 + x)
⇒ 21 = 0.6 × (30 + x)
⇒ 21 = 18 + 0.6x
⇒ 0.6x = 3
⇒ x = 5 liters.

Hence, option (d).

16. CUET-PG 2023 General MBA | Geometry, Mensuration & Trigonometry

The altitude drawn to the base of an isosceles triangle is 8 cm and the perimeter is 32 cm. Find the area of the triagle?

A.
40 cm²
B.
44 cm²
C.
46 cm²
D.
48 cm²

17. CUET-PG 2023 General MBA | Geometry, Mensuration & Trigonometry

A hemisperical bowl of internal radius 9 cm contains a liquid. This liquid is to be filled into cylindrical shaped small bottles of diameter 3 cm and height 4 cm. How many bottles will be needed to empty the bowl?

A.
48
B.
50
C.
54
D.
56

18. CUET-PG 2023 General MBA | Geometry, Mensuration & Trigonometry

A hollow hemisphere and a cone have equal bases. If their heights are also equal, then the ratio of their curved surface area will be:

A.
1 : 3
B.
√2 : 1
C.
√3 : 1
D.
5 : 1

Answer: Option B

Explanation :

Let the radius of the hemispere and cone be r.

Height of the hemispehere will also be r, hence height of the cone will be r.

Slant height of the cone (l) = $\sqrt{r^{2} + r^{2}}$ = √2 r

Curved surface area of Hemispere = 1/2 × 4πr² = 2πr²

Curved surface area of Cone = πrl = π × r × √2r = √2 × πr²

∴ Required ratio = 2πr² : √2 × πr² = 2 : √2 = √2 : 1

Hence, option (b).

19. CUET-PG 2023 General MBA | Permutations, Combinations & Probability

In how many different ways can the letters of the word 'TRANSPORT' be arranged the vowels always come together?

A.
20150
B.
20160
C.
20170
D.
20180

20. CUET-PG 2023 General MBA | Permutations, Combinations & Probability

In how many ways can a group of 5 men and 2 women be made out of a total of 7 men and 3 women?

A.
60
B.
62
C.
63
D.
68

21. CUET-PG 2023 General MBA | Permutations, Combinations & Probability

In a simultaneous throw of a pair of dice, find the probability of getting a total more than 8?

A.
5/12
B.
5/14
C.
5/18
D.
7/18

22. CUET-PG 2023 General MBA | Permutations, Combinations & Probability

A card is drawn from a pack of 52 cards. The probability of getting a queen of club or a king of heart is:

A.
1/26
B.
2/13
C.
3/26
D.
7/13

23. CUET-PG 2023 General MBA | Ratio, Proportion and Partnership

If $\frac{a}{b}$ = $\frac{4}{5}$ and $\frac{b}{c}$ = $\frac{15}{16}$ , then $\frac{c^{2} - a^{2}}{c^{2} + a^{2}}$ is:

A.
3/25
B.
6/25
C.
7/25
D.
9/25

24. CUET-PG 2023 General MBA | Ratio, Proportion and Partnership

If a + 1/b = 1 and b + 1/c = 1, then what is the value of abc?

A.
-1
B.
-2
C.
-3
D.
0

25. CUET-PG 2023 General MBA | Ratio, Proportion and Partnership

If 2x + 1/3x = 6, then 3x + 1/2x is equal to:

A.
4
B.
8
C.
9
D.
12

26. CUET-PG 2023 General MBA | Ratio, Proportion and Partnership

If a + b + c = 0, then the value of $\frac{a^{2} + b^{2} + c^{2}}{a^{2} - bc}$ is:

A.
0
B.
1
C.
2
D.
3

27. CUET-PG 2023 General MBA | Geometry, Mensuration & Trigonometry

If the area of the circle in the figure is 36π cm² and ABCD is a square, then the are of ΔACD in cm² is:

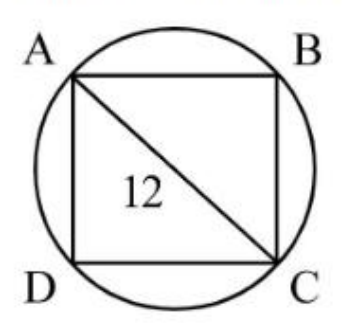
A.
12π
B.
36/π
C.
12
D.
36

28. CUET-PG 2023 General MBA | Geometry, Mensuration & Trigonometry

A piece of wire 78 cm long is bent in the form of an isosceles triangle. If the ratio of one of the equal sides to the base 5 : 3, then what is the length of the base?

A.
16 cm
B.
18 cm
C.
20 cm
D.
30 cm

29. CUET-PG 2023 General MBA | Simple and Compound Interest

A sum of money at simple interest amounts to Rs. 815 in 3 years and to Rs. 854 in 4 years. The sum is:

A.
Rs. 650
B.
Rs. 690
C.
Rs. 698
D.
Rs. 700

30. CUET-PG 2023 General MBA | Average, Mixture & Alligation

The average of six numbers is m and the average of three of these is y. If the avearge of the reamining three is Z, then:

A.
2m = y + z
B.
2y = m + z
C.
2z = m + y
D.
m = 2y + z

31. CUET-PG 2023 General MBA | Average, Mixture & Alligation

The average of five consecutive numbers is m. If the next two numbers are also included, how shall the average vary?

A.
If shall increase by 2
B.
If shall increase by 3
C.
If shall increase by 5
D.
If shall remain the same
E.
It shall increase by 1

32. CUET-PG 2023 General MBA | Average, Mixture & Alligation

In the first ten overs of a cricket game, the run rate was only 3.2. What should be the run rate in the remaining 40 overs to reach the target of 282 runs?

A.
6
B.
6.25
C.
6.75
D.
8

33. CUET-PG 2023 General MBA | Time and Work

If 5 workers can collect 60 kg wheat in 3 days, how many kilograms of wheat will 8 workers collect in 5 days?

A.
140
B.
160
C.
180
D.
200

Answer: Option B

Explanation :

We know, $\frac{M_{1} \times H_{1}}{W_{1}}$ = $\frac{M_{2} \times H_{2}}{W_{2}}$

⇒ $\frac{5 \times 3}{60}$ = $\frac{8 \times 5}{W_{2}}$

⇒ W₂ = 20 × 8 = 160 kgs.

Hence, option (b).

34. CUET-PG 2023 General MBA | Linear & Quadratic Equations

The cost of 8 pens and 14 fans is Rs. 500. What is the cost of 12 pens and 21 fans?

A.
Rs. 600
B.
Rs. 700
C.
Rs. 750
D.
Rs. 800

35. CUET-PG 2023 General MBA | Numbers

If x^y = y^x, then ${(\frac{x}{y})}^{\frac{x}{y}}$ , is equal to:

A.
x^y/x
B.
x^x/y-1
C.
1
D.
x^x/y

Answer: Option B

Explanation :

We need to given answer in terms of x, hence let us find value of y in terms of x.

Given, x^y = y^x
⇒ y = (x^y)^1/x = x^y/x

Now, ${(\frac{x}{y})}^{\frac{x}{y}}$ = ${(\frac{x}{x^{y / x}})}^{\frac{x}{y}}$

= ${(x^{1 - x / y})}^{\frac{x}{y}}$

= $x^{x / y - 1}$

Hence, option (b).

CUET-PG 2023 General MBA

Feedback