CAT 2020 LRDI Slot 1 | Previous Year CAT Paper
Answer the next 4 questions based on the information given below.
1000 patients currently suffering from a disease were selected to study the effectiveness of treatment of four types of medicines — A, B, C and D. These patients were first randomly assigned into two groups of equal size, called treatment group and control group. The patients in the control group were not treated with any of these medicines; instead they were given a dummy medicine, called placebo, containing only sugar and starch. The following information is known about the patients in the treatment group.
- A total of 250 patients were treated with type A medicine and a total of 210 patients were treated with type C medicine.
- 25 patients were treated with type A medicine only. 20 patients were treated with type C medicine only. 10 patients were treated with type D medicine only.
- 35 patients were treated with type A and type D medicines only. 20 patients were treated with type A and type B medicines only. 30 patients were treated with type A and type C medicines only. 20 patients were treated with type C and type D medicines only.
- 100 patients were treated with exactly three types of medicines.
- 40 patients were treated with medicines of types A, B and C, but not with medicines of type D. 20 patients were treated with medicines of types A, C and D, but not with medicines of type B.
- 50 patients were given all the four types of medicines. 75 patients were treated with exactly one type of medicine.
How many patients were treated with medicine type B?
Answer: 340
Explanation :
We can draw the following Venn diagram according to the information given in the question.

75 patients were treated with exactly one type of medicine.
∴ 25 + a + 20 + 10 = 75
⇒ a = 20
250 patients were treated with type A medicine
∴ 25 + 30 + 20 + 35 + 20 + 40 + 50 + e = 250.
⇒ e = 30
100 patients were treated with exactly three types of medicines.
∴ 20 + 40 + c + e = 100
⇒ c = 10
210 patients were treated with type C medicine
∴ 30 + 40 + b + 20 + 20 + 50 + c + 20 = 210
⇒ b = 20
Since patients were equally in treatment group and control group hence, there were total 500 patients who were in the treatment group and 500 in control group (who were not given any medicine).
Total patient in treatment group = 500 = 25 + 30 + 20 + 35 + 20 + 40 + 50 + e + a + b + c + d + 20 + 20 + 10.
⇒ d = 150
The completed Venn diagram:
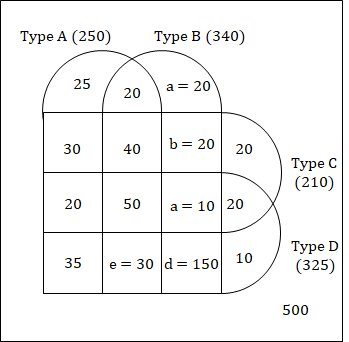
∴ 340 patients were treated with Type B medicine.
Hence, 340.
Workspace:
The number of patients who were treated with medicine types B, C and D, but not type A was:
Answer: 10
Explanation :
Consider the solution to the first question of this set.
The number of patients who were treated with medicine types B, C and D, but not type A is a = 10.
Hence, 10.
Workspace:
How many patients were treated with medicine types B and D only?
Answer: 150
Explanation :
Consider the solution to the first question of this set.
The number of patients who were treated with medicine types B and D only = d = 150.
Hence, 150.
Workspace:
The number of patients who were treated with medicine type D was:
Answer: 325
Explanation :
Consider the solution to the first question of this set.
The number of patients who were treated with medicine type D was 325.
Hence, 325.
Workspace:
Answer the next 4 questions based on the information given below.
Ten musicians (A, B, C, D, E, F, G, H, I and J) are experts in at least one of the following three percussion instruments: tabla, mridangam, and ghatam. Among them, three are experts in tabla but not in mridangam or ghatam, another three are experts in mridangam but not in tabla or ghatam, and one is an expert in ghatam but not in tabla or mridangam. Further, two are experts in tabla and mridangam but not in ghatam, and one is an expert in tabla and ghatam but not in mridangam.
The following facts are known about these ten musicians.
- Both A and B are experts in mridangam, but only one of them is also an expert in tabla.
- D is an expert in both tabla and ghatam.
- Both F and G are experts in tabla, but only one of them is also an expert in mridangam.
- Neither I nor J is an expert in tabla.
- Neither H nor I is an expert in mridangam, but only one of them is an expert in ghatam.
Who among the following is DEFINITELY an expert in tabla but not in either mridangam or ghatam?
- A.
F
- B.
A
- C.
H
- D.
C
Answer: Option C
Explanation :
We can draw the following Venn diagram based on the information given in the main paragraph.

D is an expert in both tabla and ghatam.
Since I is neither an expert in tabla nor in mridangam hence, he is an expert in ghatam
∴ D and I are the only two experts in ghatam.
Now, J is not an expert in tabla hence, he can only be an expert in mridangam only.
Also, H is not an expert in mridangam hence, he can only be an expert in tabla only.
Both A and B are experts in mridangam, but only one of them is also an expert in tabla.
Both F and G are experts in tabla, but only one of them is also an expert in mridangam.
There are two experts in tabla and mridangam only one of them is either A or B and the other is either F or G.
∴ We can make the following Venn diagram

∴ H is an expert in tabla only.
Hence, option (c).
Workspace:
Who among the following is DEFINITELY an expert in mridangam but not in either tabla or ghatam?
- A.
E
- B.
B
- C.
G
- D.
J
Answer: Option D
Explanation :
Consider the solution to the first question of this set.
J is an expert in mridangam only.
Hence, option (d).
Workspace:
Which of the following pairs CANNOT have any musician who is an expert in both tabla and mridangam but not in ghatam?
- A.
C and E
- B.
C and F
- C.
A and B
- D.
F and G
Answer: Option A
Explanation :
Consider the solution to the first question of this set.
Neither C nor E can be an expert in both tabla and mridangam.
Hence, option (a).
Workspace:
If C is an expert in mridangam and F is not, then which are the three musicians who are experts in tabla but not in either mridangam or ghatam?
- A.
C, E and G
- B.
E, F and H
- C.
C, G and H
- D.
E, G and H
Answer: Option B
Explanation :
Consider the solution to the first question of this set.
If C is an expert in mridangam and F is not, we can make the following Venn diagram.
We can make the following Venn diagram

∴ E, F and H are experts in tabla but neither mridangam or ghatam.
Hence, option (b).
Workspace:
Answer the next 6 questions based on the information given below.
In a certain board examination, students were to appear for examination in five subjects: English, Hindi, Mathematics, Science and Social Science. Due to a certain emergency situation, a few of the examinations could not be conducted for some students. Hence, some students missed one examination and some others missed two examinations. Nobody missed more than two examinations.
The board adopted the following policy for awarding marks to students. If a student appeared in all five examinations, then the marks awarded in each of the examinations were on the basis of the scores obtained by them in those examinations.
- If a student missed only one examination, then the marks awarded in that examination was the average of the best three among the four scores in the examinations they appeared for.
- If a student missed two examinations, then the marks awarded in each of these examinations was the average of the best two among the three scores in the examinations they appeared for.
- The marks obtained by six students in the examination are given in the table below. Each of them missed either one or two examinations.

The following facts are also known.
- Four of these students appeared in each of the English, Hindi, Science, and Social Science examinations.
- The student who missed the Mathematics examination did not miss any other examination.
- One of the students who missed the Hindi examination did not miss any other examination. The other student who missed the Hindi examination also missed the Science examination.
Who among the following did not appear for the Mathematics examination?
- A.
Carl
- B.
Esha
- C.
Foni
- D.
Alva
Answer: Option A
Explanation :
For the subjects missed, the student gets average of top 2 or 3 scores.
∴ Among the six students given, no students would’ve missed that subject where they get highest of the lowest marks.
Also, in the missed subject(s) the student cannot get 2nd lowest marks.
∴ For the missed subject(s), the student will get 2nd highest or 3rd highest marks.
English is missed by 2 students. These two students can only be Esha and Foni.
(For Esha and Foni English is neither highest nor lowest)
Solving for Esha:
Esha has missed English.
∴ Marks in English should be average of top three of the remaining subjects.
Average of remaining top three marks = (95 + 85 + 60)/3 = 80 (which is equal to Esha’s marks in English).
One of the students missed only Mathematics. Carl is the only one who could’ve missed Mathematics.
Solving for Carl
∴ Carl will not miss any other exam.
One of the students missed Hindi and Science. This can be either Alva or Deep since they both have same marks in Hindi and Science.
One of the students missed only Hindi. This can be either Alva, Deep since their marks in Hindi is same as average of the remaining top 3 scores.
∴ One of Alva or Deep missed only Hind and the other missed Hindi and Science.
So far we have
Alva missed ⇒ only Hindi or Hindi and Science
Carl ⇒ only Mathematics
Deep missed ⇒ only Hindi or Hindi and Science
Esha missed ⇒ only English
Alva and Deep definitely missed Hindi
Esha and Foni definitely missed English
One of Alva or Deep missed Science
We need to find one more person who missed Science and two more people who missed Social Science.
One more person who could’ve missed Science is Bithi and two more people who could’ve missed Social Science are Bithi and Foni
∴ We finally have
Alva missed ⇒ only Hindi or Hindi and Science
Carl missed ⇒ only Mathematics
Bithi missed ⇒ Science and Social Science
Deep missed ⇒ Hindi and Science or only Hindi
Esha missed ⇒ only English
Foni missed ⇒ English and Social Science
∴ Carl missed the Mathematics exam.
Hence, option (a).
Workspace:
Which students did not appear for the English examination?
- A.
Cannot be determined
- B.
Esha and Foni
- C.
Carl and Deep
- D.
Alva and Bithi
Answer: Option B
Explanation :
Consider the solution the first question of this set.
Esha and Foni did not appear for English.
Hence, option (b).
Workspace:
What BEST can be concluded about the students who did not appear for the Hindi examination?
- A.
Alva and Esha
- B.
Two among Alva, Deep and Esha
- C.
Deep and Esha
- D.
Alva and Deep
Answer: Option D
Explanation :
Consider the solution the first question of this set.
Alva and Deep both missed Hindi exam.
Hence, option (d).
Workspace:
What BEST can be concluded about the students who missed the Science examination?
- A.
Bithi and one out of Alva and Deep
- B.
Alva and Deep
- C.
Deep and Bithi
- D.
Alva and Bithi
Answer: Option A
Explanation :
Consider the solution the first question of this set.
Bithi definitely missed Science exam. One of Alva or Deep also missed Science.
Hence, option (a).
Workspace:
How many out of these six students missed exactly one examination?
Answer: 3
Explanation :
Consider the solution the first question of this set.
Esha, Carl and one of Alva or Deep missed only one exam.
Hence, 3.
Workspace:
For how many students can we be definite about which examinations they missed?
Answer: 4
Explanation :
Consider the solution the first question of this set.
Except for Alva and Deep we can determine number of exams missed for other 4 students.
Hence, 4.
Workspace:
Answer the next 4 questions based on the information given below.
The local office of the APP-CAB company evaluates the performance of five cab drivers, Arun, Barun, Chandan, Damodaran, and Eman for their monthly payment based on ratings infive different parameters (P1 to P5) as given below:
P1: timely arrival
P2: behaviour
P3: comfortable ride
P4: driver's familiarity with the route
P5: value for money
Based on feedback from the customers, the office assigns a rating from 1 to 5 in each of these parameters. Each rating is an integer from a low value of 1 to a high value of 5. The final rating of a driver is the average of his ratings in these five parameters. The monthly payment of the drivers has two parts – a fixed payment and final rating-based bonus. If a driver gets a rating of 1 in any of the parameters, he is not eligible to get bonus. To be eligible for bonus a driver also needs to get a rating of five in at least one of the parameters.
The partial information related to the ratings of the drivers in different parameters and the monthly payment structure (in rupees) is given in the table below:

The following additional facts are known.
- Arun and Barun have got a rating of 5 in exactly one of the parameters. Chandan has got a rating of 5 in exactly two parameters.
- None of drivers has got the same rating in three parameters.
If Damodaran does not get a bonus, what is the maximum possible value of his final rating?
- A.
3.6
- B.
3.2
- C.
3.8
- D.
3.4
Answer: Option A
Explanation :
Damodaran does not get bonus. Hence, either he got a rating of 1 in one of the parameters or he did not get a rating of 5 in any of the parameters.
The average rating would be maximum when he gets 2 5-star ratings long with a 1-star rating.
∴ Average rating for Damodaran = (5 + 5 + 4 + 3 + 1)/5 = 18/5 = 3.6
Hence, option (a).
Workspace:
If Eman gets a bonus, what is the minimum possible value of his final rating?
- A.
3.4
- B.
3.0
- C.
3.2
- D.
2.8
Answer: Option B
Explanation :
Since Eman gets the bonus he must have got at least one 5-star rating and no 1-star rating.
Average rating will be minimum when Eman get only 1 5-start rating, 2 2-start rating and 2 3-star rating.
∴ Average = (5 + 3 + 3 + 2 + 2)/5 = 15/5 = 3.
Hence, option (b).
Workspace:
If all five drivers get bonus, what is the minimum possible value of the monthly payment (in rupees) that a driver gets?
- A.
1750
- B.
1600
- C.
1740
- D.
1700
Answer: Option D
Explanation :
Since we have to minimize the monthly payment, we need to minimize the average rating for all the drivers.
Minimum average rating for
Arun = (5 + 4 + 3 + 2 + 2)/5 = 16/5 = 3.2
⇒ Monthly payment = 1000 + 250 × 3.2 = 1800
Barun = (5 + 3 + 3 + 2 + 2)/5 = 15/5 = 3
⇒ Monthly payment = 1200 + 200 × 3 = 1800
Chandan = (5 + 5 + 3 + 2 + 2)/5 = 17/5 = 3.4
⇒ Monthly payment = 1400 + 100 × 3.4 = 1740
Damodaran = (5 + 3 + 3 + 2 + 2)/5 = 15/5 = 3
⇒ Monthly payment = 1300 + 150 × 3 = 1750
Eman = (5 + 3 + 3 + 2 + 2)/5 = 15/5 = 3
⇒ Monthly payment = 1100 + 200 × 3 = 1700
∴ Minimum monthly payment is Rs. 1700.
Hence, option (d).
Workspace:
If all five drivers get bonus, what is the maximum possible value of the monthly payment (in rupees) that a driver gets?
- A.
1900
- B.
1950
- C.
1960
- D.
2050
Answer: Option C
Explanation :
Since we have to maximize the monthly payment, we need to maximise the average rating for all the drivers.
Minimum average rating for
Arun = (5 + 4 + 4 + 3 + 3)/5 = 19/5 = 3.8
⇒ Monthly payment = 1000 + 250 × 3.8 = 1950
Barun = (5 + 4 + 4 + 3 + 3)/5 = 19/5 = 3.8
⇒ Monthly payment = 1200 + 200 × 3.8 = 1960
Chandan = (5 + 5 + 4 + 4 + 2)/5 = 20/5 = 4
⇒ Monthly payment = 1400 + 100 × 4 = 1800
Damodaran = (5 + 5 + 4 + 4 + 3)/5 = 21/5 = 4.2
⇒ Monthly payment = 1300 + 150 × 4.2 = 1930
Eman = (5 + 5 + 4 + 4 + 2)/5 = 20/5 = 4
⇒ Monthly payment = 1100 + 200 × 4 = 1900
∴ Maximum monthly payment is Rs. 1960.
Hence, option (c).
Workspace:
Answer the following questions based on the information given below.
Four institutes, A, B, C, and D, had contracts with four vendors W, X, Y, and Z during the ten calendar years from 2010 to 2019. The contracts were either multi-year contracts running for several consecutive years or single-year contracts. No institute had more than one contract with the same vendor. However, in a calendar year, an institute may have had contracts with multiple vendors, and a vendor may have had contracts with multiple institutes. It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes.
The following facts are also known about these contracts.
- Vendor Z had at least one contract in every year.
- Vendor X had one or more contracts in every year up to 2015, but no contract in any year after that.
- Vendor Y had contracts in 2010 and 2019. Vendor W had contracts only in 2012.
- There were five contracts in 2012.
- There were exactly four multi-year contracts. Institute B had a 7-year contract, D had a 4-year contract, and A and C had one 3-year contract each. The other four contracts were single-year contracts.
- Institute C had one or more contracts in 2012 but did not have any contract in 2011.
- Institutes B and D each had exactly one contract in 2012. Institute D did not have any contract in 2010.
In which of the following years were there two or more contracts?
- A.
2016
- B.
2017
- C.
2015
- D.
2018
Answer: Option C
Explanation :
Given:
It is known that over the decade, the institutes each got into two contracts with two of these vendors, and each vendor got into two contracts with two of these institutes.
Therefore, considering point (V), A had one 3-year contract and one single-year contract. B had one 7- year contract and one single-year contract. C had one 3-year contract and one single-year contract. D had one 4-year contract and one single-year contract.
Using point (III), we can conclude that Y and W have only one-year contracts. Thus, 4 one-year contracts were with Y and W.
Using points (III) and (IV), W had two single-year contracts in 2012. Y did not have any contract in 2012. So, among Z and X, either Z has 2 contracts or X has two contract in 2012.
Using point (II) and (III), X, Y and W did not have 7-year contract. Therefore using point (I) we can conclude that Z must have had 7-year contract with Institute B. Also, another contract Z has must be a 3-year or a 4-year contract.
Case (i): Z has a 4-year contract.
Then X will have two 3-year contracts. One from 2010-2012 and other from 2013-2015.
So Z has to have two contracts in 2012. The 4-year contract must have been from 2010-2013 and the 7- year contract from 2013-2019 OR the 7-year contract must have been from 2010-2016 and the 4-year contract from 2016-2019
But in that case, there will be only 4 contracts in 2012. Therefore this case is invalid.
Thus, Z had a 3-year contract either with institute A or C. Therefore, X had one 4-year with D and one 3- year contract. As D did not have contract in 2010 and C did not have contract in 2011, A had contract in 2010-2012 with Vendor X and D had contract from 2012-2015 with vendor X. Again as institute C did not have a contact in 2011, B had a 7-year contract (2010-2016) with vendor Z and C had a 3-year contract (2017-2019) with vendor Z.
As institutes B and D each had exactly one contract in 2012, Remaining contracts must be with A and C.
Therefore, both contracts of W must be single-year contracts with institutes A and C. As D did not have any contract in 2010, Y must have had a single-year contract with B in 2010 and with D in 2019.
Thus, we have
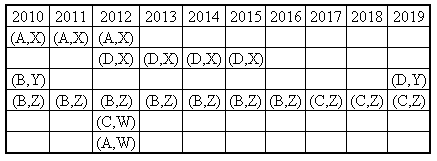
Among the given options, there were two or more contracts in 2015.
Hence, option (c).
Workspace:
Which of the following is true?
- A.
B had a contract with Y in 2019
- B.
B had a contract with Z in 2017
- C.
D had a contract with X in 2011
- D.
D had a contract with Y in 2019
Answer: Option D
Explanation :
Consider the solution to first questions of this set.

Hence, option (d).
Workspace:
In how many years during this period was there only one contract?
- A.
4
- B.
5
- C.
3
- D.
2
Answer: Option C
Explanation :
Consider the solution to first questions of this set.

Hence, option (c).
Workspace:
What BEST can be concluded about the number of contracts in 2010?
- A.
exactly 3
- B.
at least 3
- C.
exactly 4
- D.
at least 4
Answer: Option A
Explanation :
Consider the solution to first questions of this set.

Hence, option (a).
Workspace:
Which institutes had multiple contracts during the same year?
- A.
B only
- B.
A only
- C.
B and C only
- D.
A and B only
Answer: Option D
Explanation :
Consider the solution to first questions of this set.

Hence, option (d).
Workspace:
Which institutes and vendors had more than one contracts in any year?
- A.
A, B, W, and X
- B.
B, D, W, and X
- C.
A, D, W, and Z
- D.
B, W, X, and Z
Answer: Option A
Explanation :
Consider the solution to first questions of this set.

Hence, option (a).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report