Percentage, Profit & Loss - Previous Year IPM/BBA Questions
The best way to prepare for Percentage, Profit & Loss is by going through the previous year Percentage, Profit & Loss questions for IPMAT - Indore. Here we bring you all previous year Percentage, Profit & Loss IPMAT - Indore questions along with detailed solutions.
Click here for previous year questions of other topics.
It would be best if you clear your concepts before you practice previous year Percentage, Profit & Loss questions for IPMAT - Indore.
ipm
In an election with only two contesting candidates, 15% of the voters did not turn up to vote, and 50 voters cast invalid votes. It is known that 44% of all the voters in the voting list voted for the winner. lf the winner got 200 votes mote than the other candidate, then the number of voters in the voting list is
Answer: 5000
Text Explanation :
Let the total number of voters in the list be 100x.
Total voters who voted is 85% = 85x
Invalid votes = 50
∴ Valid votes = 85x - 50
Winner gets 44% of total votes = 44x
∴ Second candidates gets = 85x - 50 - 44x = 41x - 50 votes
Given in the question
44x - (41x - 50) = 200
⇒ 3x + 50 = 250
⇒ 3x = 150
⇒ x = 50
∴ Number of voters in the voting list = 100x = 5000.
Hence, 5000.
Workspace:
A goldsmith bought a large solid golden hall at INR 1 000000 and melted it to make a certain number of solid spherical beads such that the radius of each bead was one-filth of the radius of the original hall Assume that the cost of making golden beads is negligible. If the goldsmith sold all the heads at 20% discount on the listed price and made a total profit of 20% then the listed price of each golden bead. in INR, was
- (a)
12000
- (b)
48000
- (c)
9600
- (d)
24000
Answer: Option A
Text Explanation :
Workspace:
Aruna purchases a certain number of apples for INR 20 each and a certain number of mangoes for INR 25 each. If she sells all the apples at 10% profit and all the mangoes at 20% loss, overall she makes neither profit nor loss. Instead, if she sells all the apples at 20% loss and all the mangoes at 10% profit, overall she makes a loss of INR 150 . Then the number of apples purchased by Aruna is _________.
Answer: 50
Text Explanation :
Let Aruna purchase x apples at 20 each and y mangoes at 25 each.
Total cost = 20x + 25y
Case 1:
Total selling price of apples = x × 20 × 1.1 = 22x
Total selling price of mangoes = y × 25 × 0.8 = 20y
Since Aruna had no profit or loss, total cost price = total selling price
∴ 20x + 25y = 22x + 20y
⇒ 5y = 2x
⇒ x : y = 5 : 2
∴ Let x = 5q and y = 2q ...(1)
Case 2:
Total selling price of apples = x × 20 × 0.8 = 16x
Total selling price of mangoes = y × 25 × 1.1 = 27.5y
Now Aruna incurred a loss of Rs. 150
∴ 20x + 25y - 150 = 16x + 27.5y
⇒ 4x - 150 = 2.5y
⇒ 20q - 150 = 5q
⇒ q = 10
∴ Number of apples bought by Aruna = x = 5q = 50.
Hence, 50.
Workspace:
The cost of a piece of jewellery is proportional to the square of its weight. A piece of jewellery weighing 10 grams is INR 3600. The cost of a piece of jewellery of the same kind weighing 4 grams is
- (a)
INR 1220
- (b)
INR 600
- (c)
INR 576
- (d)
INR 1440
Answer: Option C
Text Explanation :
Given, price ∝ (weight)2
∴ =
⇒ = =
⇒ p2 = 3600 × 4/25 = 576
Hence, option (c).
Workspace:
In a city, 50% of the population can speak in exactly one language among Hindi, English and Tamil, while 40% of the population can speak in at least two of these three languages. Moreover, the number of people who cannot speak in any of these three languages is twice the number of people who can speak in all these three languages. If 52% of the population can speak in Hindi and 25% of the population can speak exactly in one language among English and Tamil, then the percentage of the population who can speak in Hindi and in exactly one more language among English and Tamil is
- (a)
22%
- (b)
25%
- (c)
30%
- (d)
38%
Answer: Option A
Text Explanation :
Let the number of people who speak
Exactly 3 languages = a
Exactly 2 languages = b
Exactly 1 language = c
No language = d
⇒ a + b + c + d = 100 ...(1)
Given, c = 50 and a + b = 40 ...(2)
From (1) and (2) we get, d = 10 ...(3)
The number of people who cannot speak in any of these three languages is twice the number of people who can speak in all these three languages
⇒ d = 2a
∴ a = 5 [d = 10 from (3)]
Now, 52% of the population can speak in Hindi and 25% of the population can speak exactly in one language among English and Tamil. We can make the following Venn Diagram with the information so far.
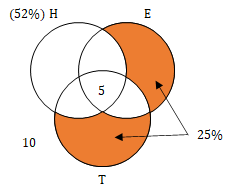
Total orange region = 25
Now, Number of people speaking exactly one language (c) = 50 = (Only Hindi speaking people) + (Only English speaking people) + (Only Tamil speaking people)
⇒ 50 = (Only Hindi speaking people) + 25
⇒ Only Hindi speaking people = 25
Also, Total Hindi speaking people = Only Hindi + (Hindi and exactly one other language) + (All three languages)
⇒ 52 = 25 + (Hindi and exactly one other language) + 5
⇒ Hindi and exactly one other language = 22
Hence, option (a).
Workspace:
A shopkeeper reduces the price of a pen by 25% as a result of which the sales quantity increased by 20%. If the revenue made by the shopkeeper decreases by x% then x is
Answer: 10
Text Explanation :
Workspace:
 Solution
Solution Discuss
Discuss Report
Report