Geometry - Previous Year IPM/BBA Questions
The best way to prepare for Geometry is by going through the previous year Geometry questions for IPMAT - Indore. Here we bring you all previous year Geometry IPMAT - Indore questions along with detailed solutions.
Click here for previous year questions of other topics.
It would be best if you clear your concepts before you practice previous year Geometry questions for IPMAT - Indore.
ipm
In a triangle ABC, let D be the mid-point of BC, and AM be the altitude on BC. If the lengths of AB, BC and CA arc in the ratio of 2:4:3, then the ratio of the lengths of BM and AD would be
- (a)
12 : 11
- (b)
12 : 11
- (c)
11 : 4√10
- (d)
11 : 12
Answer: Option C
Text Explanation :
Workspace:
The lengths of the sides of a triangle are x, 21 and 40, where x is the shortest side. A possible value of x is
- (a)
18
- (b)
20
- (c)
19
- (d)
16
Answer: Option B
Text Explanation :
The three sides are x, 21 and 40.
In a triangle:
difference of other two sides < any side < sum of other two sides.
⇒ 40 - 21 < x < 40 + 21
⇒ 19 < x < 61
Only option (b) satisfies this condition.
Hence, option (b).
Workspace:
In a right-angled triangle ABC, the hypotenuse AC is of length 13 cm. A line drawn connecting the midpoints D and E of sides AB and AC is found to be 6 cm in length. The length of BC is
- (a)
12 cm
- (b)
5 cm
- (c)
2√3 cm
- (d)
8 cm
Answer: Option A
Text Explanation :
In a triangle, the line joining the mid-points of two sides is parallel to the third side and half of it.
D and E are midpoints of AB and AC respectively. Hence, DE will be parallel to BC and half of BC.
⇒ DE = BC/2
⇒ BC = 12.
Hence, option (a).
Workspace:
If the angles A, B, C of a triangle are in arithmetic progression such that sin(2A + B) = 1/2 then sin(B + 2C) is equal to
- (a)
-1/2
- (b)
1/2
- (c)
-1/√2
- (d)
3/√2
Answer: Option A
Text Explanation :
Let the three angle of the triangle be A = a - d, B = a and C = a + d degrees.
⇒ A + B + C = (a - d) + a + (a + d) = 180°
⇒ a = 60°
∴ B = 60°
Now, Sin(2A + B) = 1/2
Since, B = 60° (2A + B) > 60°
Sin30° = 1/2 or Sin(180 - 30) = 1/2
⇒ 2A + B = 180 - 30
⇒ 2A + 60° = 150°
⇒ A = 45°
∴ C = 180 - 45 - 60 = 75°
∴ Sin(B + 2C) = Sin(210°)
= Sin(180° + 30°)
= - Sin(30°)
= - 1/2
Hence, option (a).
Workspace:
ABCD is a quadrilateral whose diagonals AC and BD intersect at O. If triangles AOB and COD have areas 4 and 9 respectively, then the minimum area that ABCD can have is
- (a)
26
- (b)
25
- (c)
21
- (d)
16
Answer: Option B
Text Explanation :
Area of triangle AOB = 4, DOC = 9, AOD = x and BOC = y
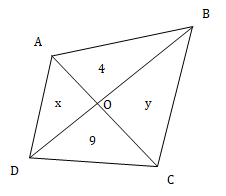
In a quadrilateral, product of area of diagonally opposite triangles is same.
∴ 4 × 9 = x × y
⇒ xy = 36
Area of quadrilateral = 4 + 9 + x + y
Now we need to minimise 4 + 9 + x + y
This is possible when x + y is least possible.
We know, AM ≥ GM
⇒ ≥
⇒ (x + y) ≥ 12
∴ Least possible value of x + y = 12
⇒ Least possible area of the quadrilateral = 4 + 9 + x + y = 25
Hence, option (b).
Workspace:
The number of acute angled triangles whose sides are three consecutive positive integers and whose perimeter is at most 100 is
- (a)
28
- (b)
29
- (c)
31
- (d)
33
Answer: Option B
Text Explanation :
Let the sides of the triangle be x, x + 1 and x + 2.
Now, x + x + 1 + x + 2 ≤ 100
⇒ 3x ≤ 97
⇒ x ≤ 32.33 ...(1)
Also, the given triangle is an acute triangle, hence
(x + 2)2 < (x + 1)2 + x2
⇒ x2 + 4 + 4x < x2 + 2x + 1 + x2
⇒ x2 - 2x - 3 > 0
⇒ (x - 3)(x + 1) > 0
⇒ x < -1 or x > 3 ...(2)
From (1) and (2), we get
x can take any value out of 4, 5, 6, ..., 31 and 32 i.e., 29 values.
Hence, option (b).
Workspace:
The sum of the interior angles of a convex n-sided polygon is less than 2019°. The maximum possible value of n is
Answer: 13
Text Explanation :
The sum of the interior angles of a convex n-sided polygon is less than 2019°. The maximum possible value of n is
Sum of interior angles of n-sided convex polygon is given by the formula (n - 2) × 180°
⇒ (n - 2) × 180° < 2019°
⇒ (n - 2) < 2019/180
⇒ (n - 2) < 11.22
⇒ n < 13.22
∴ Highest possible value of n is 13. [n has to be an integer.]
Hence, 13.
Workspace:
The number of whole metallic tiles that can be produced by melting and recasting a circular metallic plate, if each of the tiles has a shape of a right-angled isosceles triangle and the circular plate has a radius equal in length to the longest side of the tile (Assume that the tiles and plate are of uniform thickness, and there is no loss of material in the melting and recasting process) is
Answer: 12
Text Explanation :
Workspace:
A chord is drawn inside a circle, such that the length of the chord is equal to the radius of the circle. Now, two circles are drawn, one on each side of the chord, each touching the chord at its midpoint and the original circle. Let k be the ratio of the areas of the bigger inscribed circle and the smaller inscribed circle, then k equals
- (a)
2 + √3
- (b)
1 + √2
- (c)
7 + 4√3
- (d)
97 + 56√3
Answer: Option D
Text Explanation :
Workspace:
Points P, Q, R and S are taken on sides AB, BC, CD and DA of square ABCD respectively, so that AP : PB = BQ : QC = CR : RD = DS : SA = 1 : n . Then the ratio of the area of PQRS to the area of ABCD is
- (a)
1 : (1 + n)
- (b)
1 : n
- (c)
1 + n2 : (1 + n)2
- (d)
(1 + n) : (1 + n2)
Answer: Option C
Text Explanation :
Workspace:
On a circular path of radius 6 m a boy starts from a point A on the circumference and walks along a chord AB of length 3 m. He then walks along another chord BC of length 2 m to reach point C. The point B lies on the minor arc AC. The distance between point C from point A is
- (a)
(√15 + √35)/2 m
- (b)
8 m
- (c)
√13 m
- (d)
6 m
Answer: Option A
Text Explanation :
Workspace:
Three cubes with integer edge lengths are given. It is known that the sum of their surface areas is 564 cm2 Then the possible values of the sum of their volumes are
- (a)
764 cm3 and 586 cm3
- (b)
586 cm3 and 564 cm3
- (c)
764 cm3 and 564 cm3
- (d)
586 cm3 and 786 cm3
Answer: Option A
Text Explanation :
Workspace:
 Solution
Solution Discuss
Discuss Report
Report